- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematics Magazine - June 2007
ARTICLES
Solving the Ladder Problem on the Back of an Envelope
Dan Kalman
Page 163
The ladder problem is a familiar max/min exercise from generations of calculus textbooks. It asks how long a ladder can be carried around a right angle corner in a hallway of specified width. In the idealized geometric version of the problem, the ladder becomes a line segment and the hallway becomes a region R with a polygonal boundary. Here, the best known solution amounts to a reversal of the original problem: rather than determining the longest ladder that will go around the corner, we find the shortest ladder that can get stuck. In this paper we consider a different approach, that avoids this reversal. Successive positions of the segment are interpreted as members of a family of lines, and if the envelope of that family falls inside the region R then the segment will go around the corner. This leads to a simple characterization of the maximum length segment that can go around the corner.
In addition to presenting this solution to the ladder problem, the paper traces some of the history of the problem, discusses several facets of envelopes of families of curves, and considers some extensions of the ladder problem.
The Recreational Gambler - Paying the Price for More Time at the Table
Joseph Bak
Page 183
Consider a gambler who makes a series of even-money bets of fixed size until his initial fortune either reaches a predetermined goal or is entirely lost. The probability of success is the probability that he will reach his goal. The duration of play is the expected number of bets until the contest is over. This article deals with the effect on both the probability of success and the duration of play if the size of the individual bets is reduced by an integral factor. In particular, we determine when the duration of play is increased most dramatically, and we obtain an upper bound for the ratio of increased duration.
The Probability of Relatively Prime Polynomials
Arthur T. Benjamin and Curtis D Bennett
Page 196
If you choose two polynomials at random, what is the chance that they are relatively prime? We first answer this question when the polynomials are nth degree polynomials whose coefficients come from the set {0, 1} under mod 2 arithmetic. Here, for any n ≥ 1, the chance that they are relatively prime is 1/2, independent of n. In our combinatorial proof of this, the Euclidean algorithm provides a bijection between relatively prime pairs and non-relatively prime pairs. More generally, If the coefficients are chosen from a field of q elements, then the probability that polynomials are relatively prime is 1 - 1/q. The same result occurs, even when the polynomials have different degree. Moreover, if we choose a random m-tuple of polynomials, the probability that they are relatively prime is 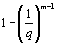 .
.
NOTES
Fitting One Right Triangle in Another
Charles H. Jepsen and Valeria Vulpe
Page 203
When does one right triangle fit in another right triangle? We give necessary and sufficient conditions on a, b, c, and d so that a right triangle with legs a and b fits in a right triangle with legs c and d.
Summary of Determinants of Matrices Over the Integers Modulo m
Jody M. Lockhart and William P. Wardlaw
Page 207
In this paper, we discuss determinants of matrices over the ring of integers modulo m for integers m ≥ 2. We derive a formula for the number of n x n matrices over this ring with a given determinant.
The Classification of Similarities, a New Approach
Aad Goddijn and Wim Pijls
Page 215
Similarity transformations in plane geometry can be divided into several types. If a similarity is not an isometry, it is either a dilative rotation or a dilative reflection. This proposition has been proved in multiple ways. A new proof is given based upon Apollonius circles.
Perfect Matchings, Catalan Numbers, and Pascal’s Triangle
Tomislav Došlic
Page 219
We evaluate the determinant of a matrix related to Pascal’s triangle by counting perfect matchings in certain classes of benzenoid graphs and derive an identity for Catalan numbers.
On Candido’s Identity
Claudi Alsina and Roger B. Nelsen
Page 226
Candido’s identity 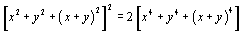 results from replacing f(z) with z2 in the functional equation
results from replacing f(z) with z2 in the functional equation

Are there other functions from the nonnegative reals to the nonnegative reals that satisfy this functional equation? Indeed there are many trivial and bizarre, highly discontinuous solutions. But if we also require f to be continuous, surjective, and satisfy f (0) = 0 , then f can only be f(z) = kz2 .
Monotonic Convergence to e via the Arithmetic-Geometric Mean
József Sándor
Page 228
In a recent note in Mathematics Magazine, Hansheng Yang and Heng Yang used the arithmetic-geometric mean inequality to prove that the sequence 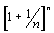 is monotonic increasing converging to e whereas
is monotonic increasing converging to e whereas 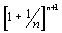 is monotonic decreasing converging to e. We provide a simpler proof using the same technique.
is monotonic decreasing converging to e. We provide a simpler proof using the same technique.




