- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematics Magazine - June 2008
ARTICLES
The Mathematics of Helaman Ferguson's Four Canoes
Melissa Shepard Loe and Jenny Merrick Borovsky
In 1997 the University of St. Thomas installed a massive granite sculpture by Helaman Ferguson outside of the new Science and Engineering Center. The sculpture consists of two linked six-foot “donuts,” each weighing more than three tons. Two pedestals support the donuts, and thirty jagged hexagons tile the ground beneath the sculpture. Why did Ferguson entitle this sculpture Four Canoes? How are the tiles and sculpture related? What rule govern placement of the tiles? And what keeps the donuts from rocking off their pedestals? In this paper, we provide an explanation of the unusual name and explore the mathematical significance of the sculpture. We discuss the link between the sculpture and the tiles, the rules governing placement of the tiles, and the question of periodicity of the tessellation. Lastly, we examine the mathematics in the construction and “fit” of the sculpture, pedestals, and tiling.
A Primer on Bernoulli Numbers and Polynomials
Tom M. Apostol
Although a large literature exists on Bernoulli numbers and Bernoulli polynomials, much of it is in widely scattered books and journals. This article serves as a brief primer on the subject, bringing together basic results (most of which are well known), together with proofs, in a manner readily accessible to those with a knowledge of elementary calculus. Some new formulas are also derived
Somewhat More Than Governors Need to Know About Trigonometry
Skip Garibaldi
In school, some of us had to memorize the values of sine and cosine at the angles 0, 30, 45, 60, and 90 degrees. Why those angles and not others? If you had to make your own table of trig values from scratch, what angles might you include? This paper shows how these questions are answered by Galois theory from standard textbooks. And it explains what this all has to do with former Florida Governor Jeb Bush.
NOTE
Pi to thousands of digits from Vieta's formula
Rick Kreminski
Vieta's 16th century infinite product formula for pi, expressed in terms of nested radicals of 2, converges surprisingly quickly: the partial product of n terms gives pi to almost exactly 0.6n digits of accuracy. From our formulation of the error, successive cancellation of smaller and smaller error terms using linear combinations of partial products computes pi to well over 0.6n(k+1) digits of accuracy, where k is the number of iterations of the algorithm. For n and k about 600, we computed pi to over 300,000 digits.
Sum Kind of Asymptotic Trouble
George W. Benthien, Keith J. Coates
When analyzing the asymptotic behavior of the sum of two or more functions, it can be easy to hoodwink oneself into making an incorrect approximation of the sum. The authors of this note found, in a well-regarded analysis book, a seemingly straightforward approximation of the sum of two terms that contains an elementary but rather subtle error. The note explains the error, how it was likely to have come about, and how to correct it.
Why are the Gergonne and Soddy Lines Perpendicular? A Synthetic Approach
Zuming Feng
In any scalene triangle the three points of tangency of the incircle together with the three vertices can be used to define three new points which are, remarkably, always collinear. This line is called the Gergonne Line. Moreover cevians through these tangent points are always concurrent at a common point that, together with the incenter, defines a second line, the Soddy Line. Why should these lines be perpendicular? Such a geometric gem deserves a synthetic geometric proof. We use the classical theorems of Ceva and Menelaus to define these lines and then establish their perpendicularity by using a certain inversion.
Golden Matrix Ring Mod p
Kung–Wei Yang
We show how to use the golden matrix ring Z(A) generated by  to prove certain identities involving Fobonacci numbers. In particular, we show that every prime divides some (and hence infinitely many) Fibonacci numbers. We also verify some generalizations and extensions of such results.
to prove certain identities involving Fobonacci numbers. In particular, we show that every prime divides some (and hence infinitely many) Fibonacci numbers. We also verify some generalizations and extensions of such results.
Geometric Proofs of the Weitzenböck and Hadwiger-Finsler Inequalities
Claudi Alsini and Roger B. Nelsen
Let a, b, and c denote the sides and T the area of a triangle. Weitzenböck’s inequality states that  , while the Hadwiger-Finsler inequalitystates that
, while the Hadwiger-Finsler inequalitystates that 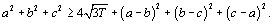 . We use the Fermat point of the triangle (the point F that minimizes the sum AF + BF + CF ) to present simple geometric proofs of both inequalities.
. We use the Fermat point of the triangle (the point F that minimizes the sum AF + BF + CF ) to present simple geometric proofs of both inequalities.
Proof Without Words
Area of a Parabolic Segment
Carl R. Seaquist
The area under the segment of a parabola is found via the volume of a pyramid.




