- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematics Magazine - October 2012
Can 17 lines produce 101 points of intersection? In how many ways? It matters how you count the ways, and how you count the points. Read about configurations of lines, Stirling numbers, dice games, football, and much else in this issue. Then check out the Problems and Reviews sections, and the problems and solutions from this year's USAMO, USAJMO, and IMO.—Walter Stromquist, Editor
ARTICLES
Perplexities Related to Fourier’s 17 Line Problem
Gerald L. Alexanderson and John E. Wetzel
In 1788 a young Joseph Fourier posed to his teacher the following little problem in geometry: arrange 17 lines in the plane so as to form 101 points of intersection, assuming there are no “multiple points”; that is, no more than two lines are concurrent. It is not difficult to show that there are just four essentially different such arrangements.
In this note we recap results we found 30 years ago and show more generally that if multiple points are permitted but no two lines are allowed to be parallel, then there are 20 essentially different such arrangements; and if both parallels and multiple points are permitted, there are 924 essentially different such arrangements. The perplexing question is what, exactly, is meant for two arrangements of lines to be essentially the same. We consider this matter briefly and conclude that we do not know how to formulate a suitable definition.
Close Encounters with the Stirling Numbers of the Second Kind
Khristo N. Boyadzhiev
This is a short introduction to the theory of Stirling numbers of the second kind S(m, k) from the point of view of analysis. It is written as an historical survey centered on the representation of these numbers by a certain binomial transform formula. We tell the story of their birth in the book Methodus Differentialis (1730) by James Stirling, and show how they mature in the works of Johann Grünert. The paper demonstrates the usefulness of these numbers in analysis. In particular, they appear in several differentiation and summation formulas. The reader can also see the connection of S(m, k) to Bernoulli numbers, to Euler polynomials, and to power sums.
Skunk Redux
David Kong and Peter D. Taylor
In the simple version of Skunk, a pair of dice is rolled again and again until either you choose to sit or at least one 1 comes up. If you sit, your payoff is the dice sum of all your previous rolls. If at least one 1 comes up while you are still standing, your payoff is zero. Here we look at an extension of the game in which you must also choose the number of dice to use and you can alter this from round to round. The simple game seems to have a straightforward enough optimal strategy but our analysis of the extension reveals flaws in our initial reasoning. Some additional extensions are considered.
NOTES
The New Rules for NFL Overtime
Chris Jones
In 2010 the NFL changed the rules for football overtime for playoff games, and in 2012 extended the change to apply to all games. We look at how the previous rule favored the team winning the coin toss with a statistically significant advantage, and then use Markov Chains to analyze the new method. It can be demonstrated that, allowing for certain assumptions about a team’s risk tolerance, the new method neatly balances out the coin toss advantage without significantly extending the expected length of the game. One other proposed technique for determining the winner of an overtime game is considered.
Combinatorial Remarks about a “Remarkable Identity”
Jørn B. Olsson and James A. Sellers
In the June 2012 issue of this magazine, Frumosu and Teodorescu-Frumosu proved that, for all integers  ,
,
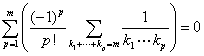
where the inner sum is taken over all p-term ordered partitions of m. Their proof is calculus-based, relying on power series manipulations. In this note, we provide a combinatorial proof of this identity (which they requested at the end of their article) and we use the insights gained via this argument to prove other results of a similar type.
An Elementary Proof of the Two-sidedness of Matrix Inverses
Frank Sandomierski
For square matrices, if AB = I then BA = I . This is proved from the fact that a homogeneous system of linear equations with more unknowns than equations has a nontrivial solution.
Heronian Triangles with Sides in Arithmetic Progression: An Inradius Perspective
Herb Bailey and William Gosnell
In this note we give a method to generate all Heronian triangles with sides in arithmetic progression (H.A.P. triangles) and show that all Brahmagupta triangles can be generated as solutions of a difference equation with certain initial conditions. The same difference equation with different initial conditions generates all rational non-integer solutions, if H.A.P. triangles whose side lengths differ from each other by 1 and also differ from the inradius by integers.
PROBLEMS
REVIEWS
NEWS AND LETTERS
41st USA Mathematical Olympiad
3rd USA Junior Mathematical Olympiad
Jacek Fabrykowski and Steven R. Dunbar
53rd International Mathematical Olympiad
Zuming Feng and Yi Sun
2012 Carl B. Allendoerfer Awards





