
Click here to open a new window with data from an experiment studying how coffee cools. This table shows the temperature of a cup of coffee over a period of 18 minutes. The coffee starts out quite hot. Its temperature at the beginning is over 40 degrees (Celsius) above room temperature But, over the course of 18 minutes its temperature drops to only 24.18 degrees above room temperature. We know from experience that the coffee will continue cooling and getting closer and closer to room temperature. Click here to open a new window with this same data in a scatter plot. This live figure enables you to compare this data with models of the form:

Use the parameter controls in this live figure to try to fit this model to the data.
In the last section we looked at linear models, models that are used to describe situations in which the change in the dependent variable is a multiple, m, of the change in the independent variable. This relationship is captured by the formula
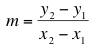
which enables us to find the constant multiplier, m, by dividing the change in the dependent variable by the change in the independent variable between any two points on the line.
The same idea is captured in words like the ones highlighted in the paragraph below.
The plan calls for the Mars Outpost to be supplied by a fleet of spacecraft that will bring 250 colonists to Mars each year. Thus, the population of Mars will rise at a rate of 250 people per year as long as there are no births or deaths.
In many situations, however, the dependent variable does not rise at a constant absolute rate but at a constant relative rate. For example --
After an initial period of ten years, we expect the Mars Outpost to be self-sustaining. In fact, even if the resupply fleet were to stop all activity we expect the population of the outpost to rise at the rate of 1.3% per year due to births.
Example:
As these words are being written the rate for a certificate of deposit at a local bank is 3.75% per year.
Questions:
Simple exponential models describe situations like this. These models are described by the family of functions:

which has two parameters. The parameter C is the value of the dependent variable, y, when the independent variable, x, is zero. The parameter b controls the relative rate at which the dependent variable changes. For example, if b = 2 then the dependent variable doubles every time the independent variable rises by 1 and if b = 0.90 then the dependent variable drops by 10% each time the independent variable rises by 1.
If we have two points, (x1, y1) and (x2, y2) on the curve

then we can determine the value of b as follows.

When we are working with data, the data is usually not exactly on the curve. Nonetheless we can use this formula to estimate the value of b. Once we know the value of b we can estimate the value of C.
Questions:
Click here to open the cooling coffee data that we looked at earlier. Answer the following questions using this data.
Click here to open a new window with a virtual laboratory in which we will examine the effects of depth on light and color. Notice the white square just above the surface of the water. Use your mouse to drag this white square below the surface of the water. Notice that at different depths its color changes and readings appear giving its depth and the intensity of three different colors of light -- red, green, and blue. These values are all 1.00 above the surface of the water. As the white square dips just below the surface of the water all three color readings drop to 0.98. This is because 2% of the light is reflected by the water's surface. All three colors are affected the same way by reflection. As the square is dragged further, however, different colors are affected differently.
At the right side of the laboratory window, the Record Data Point button enables you to record readings. Use this button to record a series of readings at the depths 0, 1, 2, ... 20 feet. You will use these readings to answer the questions below. You can copy and paste these readings to a spreadsheet by clicking and dragging your mouse to highlight the readings and then pressing CTRL-c (Windows OS) or COMMAND-c (MacOS) to copy the readings. Then open a spreadsheet, click on a blank square and press CTRL-c (Windows) or COMMAND-c (MacOS) to paste the readings into the spreadsheet. The first few readings are shown in the table below.
| Depth (Feet) | Red | Green | Blue |
| 0.98 | 0.98 | 0.98 | |
| 0.87 | 0.97 | 0.98 | |
| 0.78 | 0.96 | 0.97 |
In all of the examples above the data showed phenomenon that were decaying to zero. In many cases the data approaches a different number. Actually the raw data for the temperature of the coffee approached room temperature but we finessed this problem by working with the difference between the temperature of the coffee and the temperature of the room. This difference decayed to zero. In the next section we look at general exponential models that can be used to describe some situations in which a variable approaches a number that might not be zero.