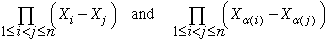
Sidebar to The Parity Theorem for Permutations
by John O. Kiltinen
[Close this window to return to the Main Article.]
I review here the transition in the pedagogical approach to the Parity Theorem over the past forty years. The reference numbers link to the entries in the References at the end of the main article -- use your Back button to return to this page.
Gallian (1998) mentions that the Parity Theorem is due to Cauchy. See Burns (1913) or Kleiner (1986) for background on Cauchy’s role in the development of group theory. Bartlow (1972), in his brief history of the Parity Theorem, gives a reference to Cauchy’s 1815 proof [Cauchy (1815), pp. 98-104], and tells that it is one of Type CJS. (See Table 1 below for the definitions of the categorizations that we are using here.)
As Bartlow points out, permutation groups first came under study because of their relevance to Galois theory, which deals with polynomials over fields, and that gives motivation for the Type P proof, in which one considers the polynomials
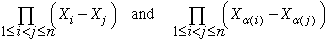
The proof rests on the observation that the second polynomial is 
times the first, depending on whether the permutation a
is even or odd. We will call it and its variants Type P proofs.
The Type P proof was once the most common used in textbooks. It is interesting to note that in the 1960s, the writers of the undergraduate texts were not necessarily satisfied with the Type P proof.
Herstein (1964) used this proof in his Topics in Algebra text. He included along with the proof on page 67 the statement,
Closely related to the Type P proof is the Type S proof, which uses the sign or signum of a permutation a defined by taking the quotient of“Frankly, we are not happy with the proof we give of this fact for it introduces a polynomial which seems extraneous to the matter at hand.”
and observes that this number is according
as a is even or odd.
This proof involves similar details, but at least it avoids bringing polynomials into the discussion. However at least one writer who used it gave hints of wishing for something simpler. Hall (1966) included the following statement about this proof:
“The reader may find the remainder of this section difficult to follow. The difficulty lies largely in the notation; the ideas are fairly intuitive, but it is unfortunately not possible to explain them with reasonable rigour without introducing symbolism which makes them appear more difficult than they in fact are. The work is kept as simple as possible and it is well worth while making some effort to understand it.”Comments such as these had some influence. Spitznagel (1968) quoted Herstein giving a variation of the Type RA proof, as did Liebeck (1969) while giving an incomplete, flawed proof with yet another approach, and also Bartlow (1972), when he gave an historical review and a Type CJs proof, like Cauchy’s original approach. Although Herstein was not satisfied with the proof, he stayed with it over the decades. The same proof is given in the 1975 second edition of Topics in Algebra and in his Abstract Algebra (Herstein, 1986), although he dropped the “not happy” statement in this new textbook.
The dissatisfaction with Type P and Type S proofs of the 1960s and the spate of journal articles that followed led to a major change in the pedagogical approach beginning in the 1980s. We have done a survey of over fifty different abstract algebra and discrete mathematics texts, mostly at the undergraduate level, dating back to the 1960s, and have characterized their approaches to the Parity Theorem. The results are presented in Table 1 below. We note that there has been a trend over the past twenty years toward proofs which stay close to the definition of parity in terms of transpositions.
Type RA (for Reduction Algorithm), the category to which our variant belongs, has been the most favored in recent years. Of the 34 texts in the survey that have first appeared since 1980, 14 (41%) have used this type of proof. Since 1990, seven of the 15 texts appearing for the first time, or 47%, have given a Type RA proof.
Of the 14 post-1980 texts that use a Type RA proof, several represent switches to this type in new editions of earlier books. For example, Fraleigh switched to Type RA in his 1982 third edition, McCoy/Janusz switched in their 1987 fourth edition, and Gallian added this type of proof in his 1990 second edition after having referred the reader to Fraleigh’s second edition for a proof in his first edition. Hillman, Alexanderson, and Grassl give this type of proof in their 1987 discrete mathematics text, which is a switch from the Type P proof in the 1978 Hillman and Alexanderson abstract algebra text. Fraleigh did not stay with Type RA beyond his third edition, switching to Type CJs in his 1989 fourth edition. He has tinkered with his approach a bit in the subsequent fifth and sixth editions.
The paper by Miller (1971) had some influence on bringing the Type RA proof into the mainstream. Saracino (1980) and Fraleigh (1982) cite this paper as the source of this type of proof, and probably other writers have picked up on it from these two texts. However Miller was not the first to find this approach to the Parity Theorem. Spitznagel (1968) does it in essentially the same way, and we see in Brenner (1957) a Type RA proof with a more complex reduction technique.
In fact, Brenner’s method is similar to my approach in that it makes the reduction by dropping two separated transpositions from a sequence which equals the identity, as opposed to two identical and adjacent transpositions gotten by a rewriting of the expression. Given this similarity to our approach, this work of over forty years ago is worthy of some comment.
Brenner observes that if 
are all distinct, then
That is, the first and last transpositions in the sequence on the left can be
dropped. Brenner does not make it clear if he is evaluating from left to right
or vice-versa, but the equation is true either way. If one evaluates from left
to right as I do, both sides of this equation reduce to the cycle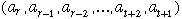 
. Evaluating right to left, one gets the inverse of this cycle.
He then goes on to take an assumed odd-length product of transpositions equaling the identity that uses a minimal number of transpositions. He does some Miller-like rewriting of this sequence to get one which has an “initial chain” of distinct entries of the sort that is subject to the reduction above, thus getting a contradiction to the minimality.
His method of dropping a pair of separated transpositions is similar to ours, but it is not as general because it assumes a shared common element between adjacent transpositions.
A Selection of Abstract Algebra and Discrete
Mathematics Texts, 1960 to 2001,
Organized According to Their Approach to the Parity
Theorem
Type RA (Reduction Algorithm) proof: Show that the identity is even by reducing by two any expression for it as a sequence of transpositions. Extend to the general result.
Type P (Polynomial) proof: Start with the polynomials in n variables
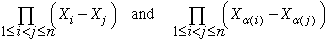
and show that the first is plus or minus the second according as a is even or odd.
Type S (Signum of a permutation) proof: Start with the sign of a permutation defined as the quotient of the expressions
and show that it is according as a
is even or odd.
Type CJs (Cycle Joining and Splitting) proof: Looks at
the cycle structure for a permutation. Shows that composing with a transposition
either merges two cycles or splits two cycles, and changes the Cauchy number
(total number moved minus the number of nontrivial cycles) of the permutation
by .
Type CI (Counting Inversions) proof: Based upon a count of the number of inversions for a permutation a, which is the number of instances of pairs (i, j) such that i < j while a(i) > a(j). Show that the parity of this count agrees with the parity of the permutation.
Type D (Determinants) Proof: A proof that relates the parity of a permutation to the sign of the determinant of the related permutation matrix.
Type NP (No Proof): The Parity Theorem is stated but not proven.
[Note: Four discrete mathematics textbooks that were reviewed included no coverage of the Parity Theorem and are therefore not listed.]
[Close this window to return to the Main Article.]