Graphing Polynomial Functions
The Microworld…
The Story…
You may browse quickly through this section if
you are familiar with polynomial functions and their graphs. It will be useful
later to familiarize you with the notation and interaction conventions we
use. The purpose of this exercise is to give some experience with polynomial
functions, and in particular to see what can be seen easily about the relationship
between the algebraic representation of a function and its graph. A function
is a convenient way to represent a relationship between two variables. When
two variables, say x and y stand for measurements of some pair of quantities
that change together in some process, and when for each value that x takes,
only one y value corresponds to it, then we say that y depends on x.
This is because we only need to
know the value of x to determine the pair. When x and y are bound together in
this way, we often say also that y is a function of x. It means the same thing.
Functions arise frequently in the models we use, and it is often helpful to
have an idea of the overall features of those functions, such as the idea
presented by the graph of the function.
Learning to guess the shape of a function graph,
starting with an algebraic function rule, is an art that requires both practice and experience.
Polynomial functions:
Let's start by reviewing what we know about linear and quadratic functions. A linear function is the function rule for an arithmetic growth model (equal changes in equal times). It has the form: and its graph is a straight line. The line graph is determined by any two of its points.
We have at the top of the
page, a utility that illustrates the fact that a polynomial function of degree
n-1 is determined by n of its points. Let's start with polynomial functions of
degree 1. In the field
type the number 2. This means that we can select 2 points on the screen to the right. Then left-click the button “Select points below”. The arrow cursor should turn into a pointing finger over the Graph2D window for selecting points accurately. After that, left-click on any two points (with different x coordinates) on the graph window. The system actually chooses the closest points with integer coordinates to the ones you picked. You see something like:
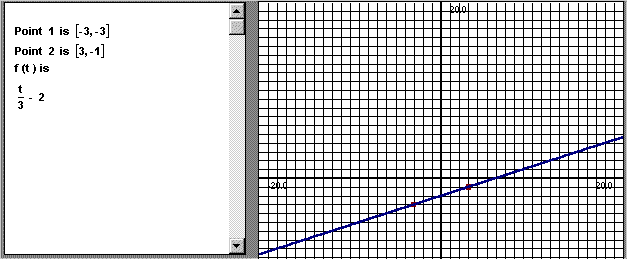
The points selected are highlighted in red, and are printed in the Math Edit window. Also, the linear function f(t) is described in exact form in that window. Finally, it is graphed in the Graph2D window. Try this for a few lines. Be certain that you understand how the slope and y-intercept of the lines can be read from the equation. When you want to clear the screen press the Reset button.
A
quadratic function is the function rule for a quadratic growth model (equal
changes in the rate of change in equal times). It has the form: and its graph is a parabola.
To see this, enter 3 in the points field:
This will allow you to select three points with different x coordinates. Again, left-click “Select points below,” and when the cursor becomes a pointing finger over the Graph2D, left-click on 3 points. You will see something like:
This
parabolic graph has a vertical axis of symmetry. It is determined by any three
of its points. Both linear and quadratic functions arise in a natural way in
the models of data and processes. In fact, the basic strategy of Calculus is to
approximate complicated function behavior by linear behavior locally. There are
several patterns that present themselves in the progression from linear to
quadratic. One is in the form of the function rule. Another is in the way that
the graph of the function is determined by its points: two points determine a
linear function, three determine a quadratic, etc.
Now we may ask whether it
is possible to extend this pattern to more "general" types of functions.
The answer is yes. And in fact, the sequence of function types that one gets
by making this extension is the most basic collection of functions in the
scientist's repertoire for modeling data. We are going to see how that goes
by an inductive extension of a simple idea. Given two pairs of data points,
and where we assume that y depends on x and that is different from ,
there is just one linear function such that
and
This function, whose graph is the line that passes through these points, is a natural linear model for that pair of points.
Similarly, given three
pairs of data points: ,
and with the x's all different, there is just one
quadratic function f(x) that satisfies: ,
,
and .
This quadratic function is a natural model for those three
data points. We are going to define polynomial functions of degree n in
a moment. A linear function will be a polynomial function of degree 1. A
quadratic function will be a polynomial function of degree 2.
Given n pairs of data
points: ,
, ,…,
with the X's all distinct, it will turn out that there is exactly one polynomial
function of degree:
such that:
, , , …. ,and
This polynomial function is
of course a natural model for the data set. One of the reasons polynomial
functions are important in modeling is that any well-behaved function at all
can be approximated by a polynomial function; the higher degree the polynomial,
the better the approximation. Needless to say, polynomial functions become
more and more complicated as their degree gets larger. But they provide us
with a rich language of mathematical models for the description of nature.
Before giving a general
definition of polynomial functions of degree n, we will see how the
determination of the functions works, and what the functions look like, both
algebraically, and graphically.
Notice three things. The three
points chosen are printed and highlighted in red. The graph is now a parabola,
and it passes through those points. And the function now has three "terms" One is
constant, one is a constant multiplied by ,
and the third is a constant (in this example, it is ) multiplied by .
This is, as we saw, the characteristic form of quadratic functions. The origin
of the word "quadratic" is in activities involved with the
calculation of areas. If it happened that the three points you chose lay in a
line, then the system reports a linear function. E.g.
The reason for this is that the coefficient of the term is 0 in this case, and therefore, the "quadratic" function is really linear. This points up an important property of polynomial functions. The polynomial functions of degree contain all the polynomial functions of smaller degree. The parabolic graph has one distinguished point: its vertex. This is where it "turns" and this is the point that lies on the axis of symmetry.
On the next page, we will begin to study the cubic polynomial functions.
