The Algebra of Cubic Numbers

The Algebra of Cubic Numbers

The Microworld…

The Story…

You may be wondering what all of this has to do with cubic equations. Well, in the previous exercise, we introduced the complex numbers: r and s. These were defined by:

and

We saw that these, together with the number 1 give all the solutions of the equation . They are the cube roots of unity, and they determine in a special way all solutions of cubic equations. To see how this is so, we abstract a little and extend the strategy of the previous page to define a new type of number: a cubic number.

Like the complex numbers, the cubic numbers have their own special algebra associated with them. In fact, mathematicians call the set of numbers we will construct: an "algebra." We will see that we may construct algebras of quartic numbers, and algebras of quintic numbers and so on in a like manner. In each case, we may establish, using the algebra, a criterion for solving polynomial equations of the associated degree.

Unfortunately, that criterion leads directly to solutions only in the cases of degree 2, 3, and 4. After that, things get complicated. To define the cubic numbers, we need a new "number" like i that we will adjoin to the complex numbers. Let us call that number J. We declare that J should be different from 1, r, and s,

and that it should satisfy the single equation (and no polynomial equation with complex coefficients of smaller degree):

If we form successive powers of J, we get . And it is not difficult to see that the totality of expressions of the form:

where a, b, and c are ordinary complex numbers will be closed under addition and multiplication, and will form a number system somewhat like the complex numbers, but with three important differences.

1) This system is "3-dimensional" That is, it requires 3 complex numbers to specify a cubic number.

2) The numbers in this system do not all have inverses (or reciprocals) as we see by observing that:

in this system, but neither factor is 0, so neither factor can have a reciprocal.

3) The complex numbers themselves already had cube roots of unity: 1, r, and . But notice that is equal to 0, and� is not.

We will call this strange system of numbers: or Cubic Numbers. It should be clear how we might alternatively define , , and so on, but here, we focus on the cubic numbers.

Like the previous exercise, this exploration will allow you to experiment with certain cubic numbers. To keep things interesting, we will consider in the exploration cubic numbers:

where a, b, and c are complex.

We will need a special notation in order to create and manipulate complex numbers. You may define complex numbers and associate them to variables just as you did in the previous exploration. You should first execute the following commands on the command line:

readfloat;
precision 7;

Then if you type:

make r complex(-1/2, sqrt(3)/2);
make s complex(-1/2, -sqrt(3)/2);
make t complex(1, 0);

you will define the cube roots of unity as complex numbers: r, s, and t. In constructing cubic numbers (whose components are always complex) you may use combinations of these variable names, or, if you prefer to supply the complex numbers on the fly, you may use the special co() function.

CO(a,b) is interpreted as:

There is a special function called Cubic() that you may use to define cubic variables in the following way. Thus, you might create a cubic number (called v) with a command like:

make v exact cubic(CO(1,0), CO(0,1), CO(1/2,-1/2));

supplying 1 for the first argument, i for the second, and for the third. Assume that you have defined the complex numbers r and s as above. If you type, say:

make w cubic(CO(1,0), r, s);

and press Enter, then the variable w is assigned to the cubic number

In fact, the system prints:

Defined: ( 1+0*i ) + ( -0.5+0.8660254*i )*J + ( -0.5-0.8660254*i )*J^2

in the Response field. This is the decimal form of the variable. If you want the exact rational form, type something like:

make v exact cubic(CO(1,0), CO(0,1), CO(1/2,-1/2));

and it prints in the response field:

Defined:

The word "exact" forces the rational form to be kept. Again, the idea is to create a few variables, and then to plot various combinations and functions of them.

As we mentioned above, you should first execute the following commands on the command line:

readfloat;
precision 7;

Suppose you have created complex variables r, s, and t, and cubic numbers v and w as above: Then you might use the special Showcubic() function (analogous to the Show function) to see the results of evaluations. For example:

showcubic(w);

returns

showcubic(v);

returns

showcubic(v^2);

returns

showcubic(v-w);

returns , and so on.

It is in general slightly difficult to compute these operations on cubic numbers by hand, but is relatively simple here. Our cubic numbers have conjugates, just as the complex numbers do. The conjugate of J is and the conjugate of is J. And in general (in the case that the coefficients are complex)

Thus,

Showcubic(conjugate(v));

returns , and

Showcubic(conjugate(w));

returns

The important property of conjugation of cubic numbers is again this:

Our special Conjugate() function may be used to calculate conjugates in the following way. If you type:

showcubic(conjugate(v*w));
showcubic(conjugate(v)*conjugate(w));

the system returns:

in both cases.

General cubic numbers (with complex coefficients) that are invariant under conjugation are called Hermitian and they play a special role in determining the discriminant condition for deciding when cubic equations with real coefficients:

(with d and e real) have 3 real solutions.

You may recall that this discriminant condition is: . We shall see why later.

Now there is one other operation that we will consider in this exploration. It is analogous to the norm operation, but is homogeneous of third degree. The new operation associates with each cubic number (whether a, b and c are real or complex) the complex number:

For those who are familiar with matrix algebra, we mention that we use the term dt to describe this function because it is in fact the determinant of the "circulant matrix"

We will show In the next section, A Remarkable Fact, that follows from the fact that DT is multiplicative, that is:

and we will give the definition for DT() which establishes its basic invariance properties and makes it the cornerstone of our applications to cubic equations.

Now when v is a cubic number, is a complex number. Thus for v defined as above,

if you type:

show(DT(v));

You will see a "picture" of the complex number

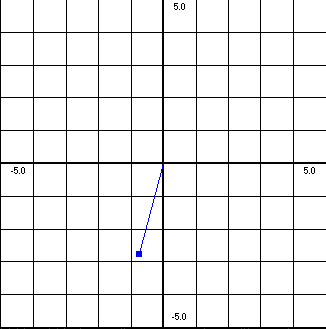
as well as its value

Now we will think of cubic numbers like the cubic number v, both symbolically as expressions like

and also as polynomial (quadratic) functions. Thus, we might represent v as

polynomial function in J:

Let's do an experiment that will anticipate the discussion of A Remarkable Fact in the next section. Create a complex function that represents the cubic number v as a polynomial in J. (Recall that since it is complex, we must use the special form below.)

make function f (ma x) of type matrix id+CO(0,1)*x+CO(1/2,-1/2)*(x^2);

Now calculate the complex number obtained by applying "v" to each of the cube roots of unity and taking the (complex) product of the results.

show(f(s)*f(r)*f(t));

The system prints:

This is the decimal approximation to DT(v) reported earlier!

The remarkable fact that these determinant invariants can be calculated as the product of the application of the cubic number v (as quadratic polynomial) to the cube roots of unity sits at the center of our approach to solving cubic equations.

In fact, starting with a cubic polynomial equation:

we will seek a cubic number w related to P in the following way. Let I be the cubic number 1, that is,

I =

Then we will seek w so that for complex variable x,

is satisfied.� This is, of course, a characteristic equation.

In the next Chapter, A Remarkable Fact, we will see that it is enough to find a cubic number w such that

P(w) = 0

It happens to be easier to do this, than to look directly for complex solutions x. And when we find such a w, it will lead to complex solutions to the cubic equation on a simple way. This generalizes to all degrees, but for degree n where n is 5 or higher, it is (shall we say) difficult to produce an associated "n-thic" number. Not surprising!

We finish with an exercise that will be helpful for understanding the beginning of the next section.

Exercise: Define an arbitrary polynomial called p[x] (with real coefficients for simplicity).

We use as an example,

Now if is a cubic number (thought of as a quadratic polynomial), we may substitute or s to get a complex number, , ,or . Here, t, r, and s are the cube roots of unity defined above.

We may also apply p to w itself to get a cubic number: .

And then we may apply that cubic number to t, r, or s as before. Thus choose some of your favorite cubic numbers w(j) and show that in every case,

But if y is different from t, r, or s, in general!

This expresses the fact that evaluation at a cube root of unity defines a mapping from the cubic numbers to the complex numbers that preserves products. That is, the mapping for fixed complex z from the complex polynomial algebra :

is an algebra homomorphism (in particular, is multiplicative) and is well-defined on the quotient algebra, the cubic numbers,

when z is a cube root of unity.

We will not attempt to prove it here (although the proof is routine in the context of Abstract Algebra). Instead, we will give you the opportunity to experiment with the fact, and perhaps find your own proof.

A scenario might go: Create a cubic number

make v exact cubic(CO(1,0),CO(0,1),CO(1/2,-1/2));

returns

Next, create the "identity" cubic number I described above. We call it K because the name I is already taken.

Make K exact cubic(CO(1,0),CO(0,0),CO(0,0));

returns:

Apply to the cubic number

showcubic(K+v+v^2+v^3+v^4);

returns

Now, substitute r for J in the resulting cubic number result to get

show(CO(55/4,27/4)+CO(-11/2,23/2)*r+CO(1/4,-7)*r^2);

returns:

Next, do it the other way. Substitute r for J in v

show(CO(1,0)+CO(0,1)*r+CO(1/2,-1/2)*r^2);

returns:

Set this to a complex number

make cc complex(-.5490381,-.6830127);

returns: Defined:

Finally, apply to the complex number to get

show( CO(1,0)+cc+cc^2+cc^3+cc^4);

returns

Done! Try this for s, and for t. Next, try it for any different complex number.