Real Roots of Cubic Equations
The Microworld...
The Story...
We finish this story with an interesting exercise. We saw that every cubic function: may be transformed by a linear change of variable: to . In the latter form, the abscissa of the inflection point is 0, so the average of the roots of the new equation is 0.
So let us
consider the simplified case of a "traceless" cubic polynomial (with
real coefficients) of the form:
. We know that this is the characteristic polynomial of traceless, Hermitian cubic number w of the form: if and only if . And the latter is true if and only if there is a single complex number a with the properties that:
|
|
Here, is the “real part” of that is
This
complex number a characterizes the three zeros of the cubic. As we saw,
those zeros will be
where is a primitive cube root of unity.
These are
the projections of three equally spaced points on a circle centered at the
origin of radius .
But notice that from the first condition above: . Now the derivative of our polynomial: has two real zeros if p has 3 real zeros. And those zeros are symmetrically placed about the origin. They are ± |a|. They occur of course at the critical points of p, the local maxima and minima. So we have another remarkable fact: If is a cubic with all roots real (hence with all coefficients real) then
- The local maxima and minima of are symmetrically placed about the origin at a distance on either side of the origin.
- And the zeros of are the projections of 3 equally spaced points from the circle of radius centered at the origin.
This is only true if all three roots are real. We will do the experiment on this page to see this interesting thing.
Click inside the cusp on the right of the screen,
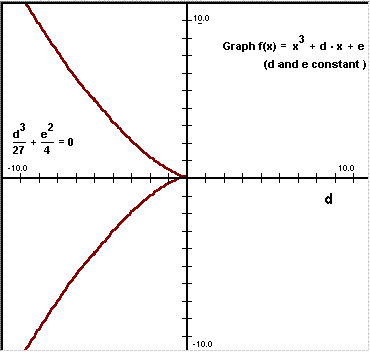
and a cubic such as will be drawn. Two vertical red lines will be drawn through the abscissas of the local maximum and minimum. Each line is at a distance from the origin.
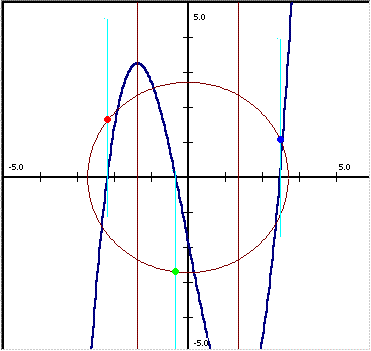
Next, a
circle centered at the origin of radius is drawn.
The three
roots of the cubic will be the projections of 3 equally spaced points on this
circle. Initially, the points at
radians are selected. You may "rotate" these points by clicking
on the scroll bar.
Watch the
points move around the circle, and as they do, a number is printed in the text
field in the lower center of the screen. The closer that number is to 0, the
closer you are to having the triple of points that project to the roots. You
may make fine adjustments to the rotation angle by clicking the scroll bar,
then using the arrow keys to rotate. When it is as close as it can get, you
will hear a "ding" and that means you found the correct triple. The
thing to think about is what happens if only one root is real.
End
of Story
