Figure 8: Euler's Elegant Example
[Open a dynamic GeoGebra applet in a new window]
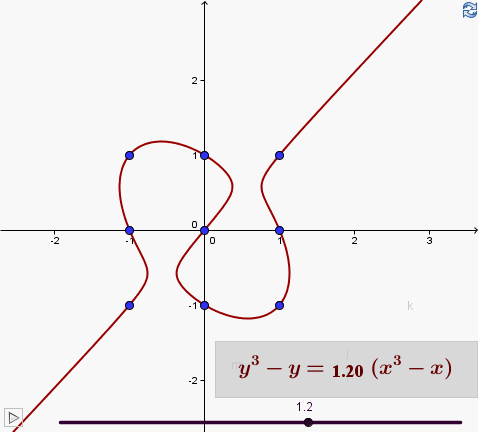
Consider the cubic equation for Euler's Elegant Example: \[ t(y^3-y) = s(x^3-x). \] As long as \( t \ne 0 \), we can divide through by \( t \). If we then let \( \displaystyle p=\frac{s}{t} \), we have the parameterized cubic equation: \begin{equation} y^3-y = p(x^3-x). \label{ParameterCubic} \end{equation}
Now for any real number that we assign to the parameter \( p \), we have an equation whose graph passes through the nine points of the \( 3 \times 3 \) grid. You can explore these curves using the applet in Figure 8. You can set particular values of \( p \) using the slider control, or put the applet into play mode and watch as the \( p \) cycles through values between \( -5 \) and \( +5 \).

For the particular values \( p=0 \), \( p=1 \), \( p=-1\), we can factor the parameterized cubic equation into factors of lower order.
| Value of \( p \) | Factorization | |
| \( -1 \) | \( (y+x)(y^2 - xy + x^2 -1)=0 \) | |
| \( \; \; \; \; 0 \) | \( y(y-1)(y+1)=0 \) | |
| \( \; \; \; \; 1 \) | \( (y-x)(y^2 + xy + x^2 -1)=0 \) | |
In the case \( p=0 \), the graph consists of three horizontal lines: \( y=0 \), \( y=1 \) and \( y=-1 \). If \( p=1 \), the graph consists of the line \( y=x \) and a conic section, namely a skewed ellipse with its major axis on the line \( y=-x \) and its minor axis on the line \( y=x \). The case \( p=-1 \) is similar, with the roles of the lines \( y=x \) and \( y=-x \) reversed. For all other values of \( p \), the equation can't be factored over the real numbers and the curve consists of a single continuous line.
There is one more important special case, when \( t=0 \) in the original equation for Euler's elegant example. In this case, we have \( x(x-1)(x+1) = 0 \), so that the graph consists of three vertical lines: \( x=0 \), \( x=1 \) and \( x=-1 \). This is the asymptotic case to which the parameterized cubic equation tends when either \( p \rightarrow +\infty \) or \( p \rightarrow -\infty \).