Special Relativity and Conic Sections - Planes Intersecting Cones

  Mathwright Microworld for this page

---

I will develop the relationship between the plane-slicing-cone picture and the focus-locus and focus-directrix properties in three stages. On this page, I sketch in a special case the strategy that I will use in 3-dimensional Euclidean Geometry.

Recall that we use a "standard" cone in Euclidean space given by the equation

,

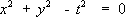as shown in the picture at the right. (Later we will interpret such a picture as a "light cone" at the origin event.) The axes are of course, orthogonal in the Euclidean metric.

Next, consider the hyperboloid (see the next figure below) defined by the equation

.

We know that each point in the interior of the cone determines a plane. Our special case will consist in choosing to belong to the upper half of the hyperboloid. (In special relativity, this hyperboloid has special significance.)

For an arbitrary choice of A and B, select the point  =  on the hyperboloid. Let , and assume that . The plane tangent to the hyperboloid at that point intersects the cone in an ellipse.

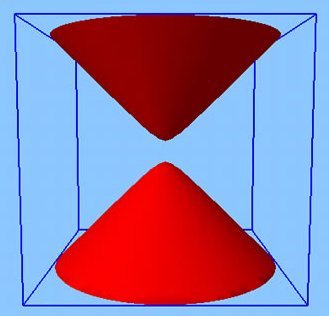
I explain in Note 2 that the center of this ellipse is  , and that it has semi-major axis of length

generated by at and semi-minor axis of length 1, generated by at .

Note 2. The Apollonian ellipse in standard form

From this, it is easy to calculate that the foci are at points:

Now this calculation tells us nothing about the focus-locus or the focus-directrix properties of . In fact, there is no directrix evident in the construction. For these, I consider a different ellipse.

Consider the plane (the plane) that is perpendicular to the axis of the cone and passes through the vertex, and let be the Euclidean orthogonal projection to this plane. Then the ellipse that I consider is the projection of to the plane. I denote that projection .

In Note 3, I show that is an ellipse. First, I represent the curve implicitly, and then I use an explicit parametric representation to cast it, after translation and rotation, in the form

,

for some .

Note 3. The projected curve is an ellipse in standard form.

Notice that there is a natural choice for the directrix for this ellipse, which I will justify below. Consider the intersection of the tangent plane, the graph of a function of x and y,

,

with the plane . Since we assume that , this intersection is the line

.

Special relativity will establish that has the focus-locus property, and that the line is the directrix for for which the focus-directrix property is true. We will see that on the Interpretation of the Experiment page.

Characterization of similarity classes of ellipses

We are now in a position to describe the similarity classes of (noncircular) ellipses in the plane. These classes are overspecified by requiring that they have

1. a focus at the origin (0, 0),
2. center at a point ,
3. semi-minor axis of length 1 (and therefore semi-major axis of length ).

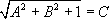It is enough in fact to choose the center and then to select the point = on the hyperboloid . The plane tangent to the hyperboloid at that point intersects the cone in the ellipse . And then the projection will satisfy the three conditions above. We will then also know the directrix and the eccentricity of , as we shall see.

If we let the unit vector , so that , we can picture the sequence of three points

as the points in the plane at times 0, 1, and 2 occupied by a uniformly moving object with (classical) velocity . When this picture is interpreted relativistically, we will also have an interpretation of the ellipse itself, as well as the focus-locus and focus-directrix properties.

In the following picture I specified only the point , the tip of the red arrow, to determine the light blue ellipse and its directrix and foci.

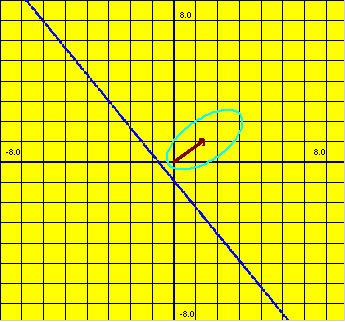
In Note 4 I interpret the directrix and eccentricity in this Euclidean setting. Later I will give the relativistic interpretation.

Note 4. Directrix and eccentricity of the projected ellipse

When we interpret the ellipse dynamically using special relativity, we can conclude that is the eccentricity of the ellipse characterized above. As mentioned, special relativity will establish that has the focus-locus property and that the line is the directrix for for which the focus-directrix property is true.

Here is the bridge between this Apollonian plane-slicing cone picture and the focus-locus picture:

Every ellipse that we construct via the process belongs to some hyperboloid

.

The planes that are tangent to the unit hyperboloid , as in the calculation above, form a special class. Their intersections with the cone will be called "boost intersections" -- they come from the case k = 1. Therefore, the ellipse obtained in the general case is simply a scalar multiple of a boost intersection. Scalar multiplication preserves similarity, and so every slice intersection is geometrically similar to a unique boost intersection.

Now I will interpret the focus-locus and focus-directrix properties, not for the slice intersections , but for their orthogonal projections under to in the plane perpendicular to the axis of the cone. The physical picture is simplest when we study a boost intersection, but it is easy to extend to all slice intersections.

Since the focus-locus and focus-directrix properties of ellipses are properties of their similarity classes , it is enough to establish and interpret them for the projected ellipses just studied. To do that, we must now recognize that the ellipses arising in this case (and in general, in fact) are "conic intersections." For that, I will develop the hyperbolic geometry I need on the next page, Hyperbolic Geometry of 2+1 Spacetime.

It is easy to see that for a general point , say, , the construction gives an ellipse whose eccentricity is , since scalar multiplication by transforms , and the latter gives a boost intersection with .