Exploration: Exponential Functions and Derivatives
General exponential functions, of the form f(x)=Cekx, can be graphed using just two points (x0,y0) and (x1,y1) on the graph of the function.
Tom Leathrum is Associate Professor of Mathematics at Jacksonville State University. He is also an Associate Editor of this Journal.
If the two points are on opposite sides of the x-axis, then there is no graph drawn. This is because of the relationship between the constants, C and k, and the points, (x0,y0) and (x1,y1), on the graph.
In the equation y=Cekx, the two constants C and k determine the shape of the graph. These two values are fixed, given two points (x0,y0) and (x1,y1) on the graph. To see how these two points determine the values of C and k, plug the two points into the equation separately:

Now solve each of these equations for C:
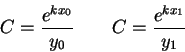
Since both equations represent C in terms of the other variables, set the right hand sides equal --- this eliminates the constant C from the equations:

Now solve this equation for k -- first, rewrite the equation a bit:

Now take natural logarithms on both sides:

This is where it is important that the two points (x0,y0) and (x1,y1) be on the same side of the x-axis -- in other words, that y0 and y1 have the same sign, so that y1/y0 is positive and the logarithm on the left hand side is defined. If y0 and y1 have the same sign (which can be checked with the inequality y0y1>0) then ln(y1/y0) =ln(|y1|)-ln(|y0|) by properties of logarithms, with the absolute values guaranteeing that the logarithms will be defined even if y0 and y1 are negative. Some care must be taken at this point to check the inequality y0y1>0, though, since this expression with the absolute values no longer requires y0 and y1 to have the same sign.
Continuing to solve for k, the equation now looks like:

Solving this algebraically for k:

It is interesting to notice that the above equation resembles the slope of a line.
Now that the value of k is known (from the points (x0,y0) and (x1,y1)), finding C is easier: plug either point into the equation y=Cekx -- plugging in (x0,y0) gives y0=Cekx0. Now divide both sides by ekx0 to solve for C:

These formulas for C and k depend only on the two points (x0,y0) and (x1,y1).
© 2001 by Tom Leathrum -- additional copyright information
Published January 2001
Exploration: Exponential Functions and Derivatives - Graphing Exponential Functions
General exponential functions, of the form f(x)=Cekx, can be graphed using just two points (x0,y0) and (x1,y1) on the graph of the function.
Tom Leathrum is Associate Professor of Mathematics at Jacksonville State University. He is also an Associate Editor of this Journal.
If the two points are on opposite sides of the x-axis, then there is no graph drawn. This is because of the relationship between the constants, C and k, and the points, (x0,y0) and (x1,y1), on the graph.
In the equation y=Cekx, the two constants C and k determine the shape of the graph. These two values are fixed, given two points (x0,y0) and (x1,y1) on the graph. To see how these two points determine the values of C and k, plug the two points into the equation separately:

Now solve each of these equations for C:
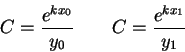
Since both equations represent C in terms of the other variables, set the right hand sides equal --- this eliminates the constant C from the equations:

Now solve this equation for k -- first, rewrite the equation a bit:

Now take natural logarithms on both sides:

This is where it is important that the two points (x0,y0) and (x1,y1) be on the same side of the x-axis -- in other words, that y0 and y1 have the same sign, so that y1/y0 is positive and the logarithm on the left hand side is defined. If y0 and y1 have the same sign (which can be checked with the inequality y0y1>0) then ln(y1/y0) =ln(|y1|)-ln(|y0|) by properties of logarithms, with the absolute values guaranteeing that the logarithms will be defined even if y0 and y1 are negative. Some care must be taken at this point to check the inequality y0y1>0, though, since this expression with the absolute values no longer requires y0 and y1 to have the same sign.
Continuing to solve for k, the equation now looks like:

Solving this algebraically for k:

It is interesting to notice that the above equation resembles the slope of a line.
Now that the value of k is known (from the points (x0,y0) and (x1,y1)), finding C is easier: plug either point into the equation y=Cekx -- plugging in (x0,y0) gives y0=Cekx0. Now divide both sides by ekx0 to solve for C:

These formulas for C and k depend only on the two points (x0,y0) and (x1,y1).
© 2001 by Tom Leathrum -- additional copyright information
Published January 2001
Exploration: Exponential Functions and Derivatives - Calculating the Derivative
To compute the derivative of the function f(x)=ex, use the definition of the derivative as a limit of a difference quotient:
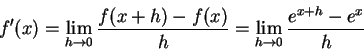
This limit can be simplified using properties of exponents:

Now, in the numerator, factor out the common ex:
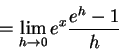
Since the limit is with respect to the variable h, and the variable x is independent of h, the ex may be treated as a constant factor and removed completely from the limit:
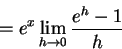
The remaining limit (not including the ex factor) is the critical limit for finding the derivative of f(x)=ex -- if this limit exists and is equal to K, then f '(x)=K ex. It remains only to find K (if it exists). For the purposes of plugging into the applet below to find K, rewrite the limit in terms of the variable x instead of h:
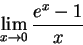
Now use the tables in the applet below to approximate the value of K.
From these tables, it seems that K=1. This is an approximation to K using the values in the tables from the applet, but it seems to be a good approximation, given the trends in the tables. If this is the case, then (from above)
This formula is important enough to bear repeating:
Exploration: Exponential Functions and Derivatives - The Derivative and Tangent Lines
With the formula for the derivative of f(x)=ex giving f '(x)=ex, the derivative can be used to find slopes of tangent lines to the graph of the function f(x)=ex. At a point (x0,y0) on the graph of f(x) (so that y0=f(x0)), the line tangent to the graph will have slope m=f '(x0). Plugging into the Point-Slope form equation for a line, then, the equation for the tangent line at (x0,y0) will be:
y-f(x0)=f '(x0) (x-x0)
This is the equation used to find the tangent lines to the graph in the applet below. Using the functions f(x)=ex and f '(x)=ex, the applet shows the tangent line for any given value of x0 in the graph, starting below with x0=1.
Other values for x0 (shown in the "x=" field in the applet) can be chosen either by entering a new value into the "x=" field or by clicking and dragging the mouse on the graph.
Exploration: Exponential Functions and Derivatives - How [i]NOT[/i] to Compute the Derivative
One very common mistake in computing the derivative of the exponential f(x)=ex is to use the Power Rule for derivatives, rather than the formula f '(x)=ex. To see why the Power Rule does not work, consider what the resulting derivative would be, using the Power Rule: f '(x)=x ex-1 (please keep in mind that this is incorrect). Using the functions f(x)=ex and f '(x)=x ex-1 in the same applet as on the previous page, it is easy to see that the values of this "derivative" do not give slopes of tangent lines to the graph of f '(x):
So be careful, when computing the derivative of an exponential function, to use the correct formula:
Exploration: Exponential Functions and Derivatives - A Simple Differential Equation
The formula for the derivative of the natural exponential function f(x)=ex was worked out on Page 2 of this exploration, and the formula says that f '(x)=ex. This is a curious relationship, though -- f(x) and f '(x) are both the same function, f(x)=f '(x)=ex. This relationship can be expressed as a differential equation by noticing that if y=f(x)=ex, then y '=f '(x)=ex =f(x)=y, or in a more concise form, y '=y. For this differential equation, y '=y, the function y=f(x)=ex is a particular solution, but there are other solutions. For example, if y=g(x)=3ex, then y '=g '(x)=3ex=y also. In fact, the general solution to the differential equation y '=y has the form y=Cex, where C is a constant. The value of C can be determined by knowing the position of one point on the graph of the solution function, as can be seen with the differential equation y '=y in the following applet:
However, on Page 1 of this exploration, the graphs of exponential functions required two points to determine the graph -- this was because the equation there, y=Cekx also included the undetermined constant k, and a second point was needed to determine both C and k. For a function h(x)=ekx, the derivative h '(x) can be computed using the above formula for the derivative of f(x)=ex, along with the Chain Rule for derivatives, to get h '(x)=kekx, which satisfies the differential equation y '=ky. The general solution of the differential equation y '=ky is y=Cekx, the same equation as on Page 1 of this exploration. As examples, look at y '=2y (k=2) and y '=y/2 (k=1/2) in the above applet.