Ideas in Mathematics is a liberal-arts mathematics course at the University of Pennsylvania, taken by many humanities, nursing, and elementary education majors to satisfy a distribution requirement. Over the last several semesters, I have been teaching two versions of the course. The first is a regular, "in-class" version for Penn undergraduates. The other is an online "distance learning" course for a varied audience consisting of high school students, adult continuing education students, Penn alumni, and a few regular Penn students. The online version involves weekly webcasts in place of regular class sessions and features chatroom-based office hours. Both versions rely on a suite of web-based courseware for student collaboration, communication, and assessment. For the in-class version I have relied on the Blackboard system, and for the distance learning version I have been using software developed by eCollege.

Dennis DeTurck is Professor of Mathematics at the University of Pennsylvania.

The goal of the course is to get every student excited about and involved in at least one aspect of the mathematics that we do. The curriculum of the course is loosely based on the COMAP textbook, For All Practical Purposes, involving strands that include

• graph theory,
• number theory,
• combinatorics,
• probability and statistics,
• geometry and fractals,
• game theory,
• voting and apportionment,
• data encoding, and
• encryption.

Often two or more of the strands are running simultaneously, in an effort to appeal to most of the students at least some of the time -- and to address the related issues of impatience and short attention spans! For example, the course begins with graph theory -- which is covered in the COMAP book -- and number theory -- which is not.

The point of this article is not to describe the distance learning or e-communication aspects of the course, but rather to describe one of the strands that runs through and supports the entire course, simultaneously providing a medium for experimentation with various concepts and, more importantly, a framework for mathematical thinking. The advertised purpose of this strand is to teach a little web-based programming in HTML and Javascript. The deeper purpose is to involve students in the highly mathematical activity of programming and -- as a subconscious byproduct -- proving theorems.

Throughout the course, students engage in activities that simultaneously

• prepare them to write their own programs,
• teach the mechanics of web-based programming, and
• force them to think algorithmically and/or reinforce or extend mathematical concepts from other strands of the course.

This is done in several "phases" in the course of the semester. In the following sections, I describe each phase, together with the corresponding activities.

Published July 2001

© 2001 by Dennis DeTurck

 

Phase I-A: Games against the computer

One thread at the beginning of the course is number theory. My immediate objective is to get students thinking and writing with a degree of mathematical precision. This is encouraged through two kinds of activities early in the course, one of which is described here and one in the next section.

The first student activity -- which actually continues through much of the semester, because some of the students enjoy it a lot -- is playing mathematical games against the computer. These games are programmed in Javascript, so they serve later as examples of working web-interactive programs. Except for the balance game (essentially a one-player game), these are simple two-player games and have strategies for one player or the other to win. Students' initial objective is to develop a winning strategy and write it up (in English) as precisely and completely as they can. Their "loose ends" are pointed out to them, e.g.,

• Should you go first or second?
• Every time, or are does it depend on the starting position of the game?
• Does your strategy cover every possible situation, even if your opponent plays irrationally?

They then make a great deal of progress at tightening up their arguments, which take on the character of mathematical proof.

The first Phase IA game is Basic Nim. In this game there are two piles of stones, and the players take turns removing any number of stones from one or the other of the piles. The object is to be the player who removes the last stone. After playing the game a couple of times against the computer, students quickly get the idea that on every turn you want to leave the same number of stones in each pile. This allows introduction of the notion of an "invariant" of the game, namely, the difference between the sizes of the piles. The simplest way to describe the winning strategy is

• go first if the invariant is nonzero at the start, otherwise go second,
• on each move, take enough stones from the larger pile to make the piles equal.

A good exercise is to write a paragraph that explains why this strategy always wins.

Later in the semester, students can try their hand at Extreme Nim. In this version, there are three piles of stones rather than two, and the strategy for winning is more complicated. The invariant this time has to do with the binary representations of the numbers of stones in each pile. A winning position is one where the sum of the i-th binary digits of the sizes of the three piles is even for all i. I use this game in conjunction with the unit on coding and data transmission schemes, since it is an example where binary arithmetic comes up unexpectedly but naturally. I also encourage students to collaborate on trying to find a strategy for this game, since it is difficult.

Other, simpler games are the December 31 game and the 20 game. In December 31, the date begins as January 1, and players alternate either increasing the month or the day of the month. (So from January 1, legal moves would include April 1 and January 12.) The winner is the player who says "December 31." After playing the computer a few times, most students realize that the invariantof the game is the day minus the number of the month, and the winning positions have the invariant equal to 19 -- as it is at the end of the game.

The second such game is 20, which starts at 0, and the players alternately increase the number by either 1 or 2. So the invariant is the remainder mod 3, and a winning position is one that leaves remainder 2 on division by three. (We study modular arithmetic when we look at data encryption.) The 21 variation of this game is interesting because the correct strategy here is to go second rather than first.

In a more mathematical light, students play a game of trying to guess an unknown weight on a balance, which paves the way for our study of the Euclidean algorithm. Many other algorithms encountered in the course are similarly illustrated using this kind of game, and the students become quite adept at explaining in great detail (and with great precision!) how they beat the games, and thus the idea of an algorithm is made plainer to them.

Phase I-B: Building tables

The second kind of activity is class-wide (or relatively large-group) collaboration on the construction of HTML tables. On the one hand, the contents of these tables support some other aspect of the mathematical activity of the class and provide data on which students can test conjectures. On the other, they give students a first experience with studying and editing the HTML source code for a webpage, using some of the basic HTML tag syntax, and managing whatever logistics are necessary to post the edited page to the web. To get this kind of activity started, a template is posted for the students to extend. It is important to include an "author" column for each row of the table.

Some diligence is required on the part of the instructor here. As the tables grow, occasionally there are students who forget to use a simple text editor and use instead some standard Web authoring tool such as Microsoft’s Front Page. This is easy to detect, because the size of the posted file typically jumps by a factor of more than three. It is important that this be caught and corrected before other students download the "corrupted" file. Of course, the other aspect that must be diligently checked -- and to some extent the students will do this themselves if they are encouraged -- is the correctness of the data in the tables.

The first "Phase IB" table I assign supports the number theory thread in the course. It is simply a table of prime factorizations, lists of divisors, number D(n) of divisors, and sum S(n) of divisors for each integer. Each student is responsible for adding at least 3 or 4 more rows to the table, depending on the size of the class. The object is to get more than a hundred rows in the table so that there is enough data for the students to detect patterns, e.g.,

• For which n is D(n) an odd number?
• What is S(n) if n is a power of 2?)

Here is the template for this table:

Number	Prime factorization	Divisors	D(n)	S(n)	Author
1	1	1	1	1	Dr. D
2	2	1, 2	2	3	Dr. D
3	3	1, 3	2	4	Dr. D
4	22	1, 2, 4	3	7	Dr. D
5	5	1, 5	2	6	Dr. D
6	2 * 3	1, 2, 3, 6	4	12	Dr. D
7	7	1, 7	2	8	Dr. D
8	23	1, 2, 4, 8	4	15	Dr. D
9	32	1, 3, 9	3	13	Dr. D
10	2 * 5	1, 2, 5, 10	4	18	Dr. D
11	11	1, 11	2	12	Dr. D
12	22 * 3	1, 2, 3, 4, 6, 12	6	28	Dr. D

 

Later in the semester, I use a table concerning "Egyptian fractions" (reciprocals of integers) -- the problem is, "For each n, find two distinct positive integers x and y so that 1/n = 1/x + 1/y." Of course, this problem can be solved pretty easily by partial fractions, but it provides more practice with HTML -- and students begin to get a little more creative with fonts, etc. Also, the little bit of algebra required to prove that the problem can always be solved is a good review.

Another interesting problem, for which the students can collect data in tabular form, is "Which (positive) integers can be expressed as the sum of two or more consecutive (positive) integers?" Data are collected in a table that begins

n	Situation	Author
1	Cannot be done	Dr. D
2	Cannot be done	Dr. D
3	1+2	Dr. D
4	Cannot be done	Dr. D
5	2+3	Dr. D
6	1+2+3	Dr. D

Students work collaboratively on this problem in an electronic threaded discussion, as well as by constructing the table. They quickly realize that the odd numbers are easy, and begin to come to grips with the others. It is difficult to prove that it can be done for all numbers except the powers of two, but there have always been a couple of students who work very hard and get at least very close to the complete proof.

Phase II: Making HTML pages with links and pictures,
using Web-based calculators, and examining source code

As with Phase I, students engage in two different kinds of activity during Phase II. In the first, students write their own simple webpages. They learn to handle text, links and images. Usually there are a few HTML aficionados in the class who can serve as consultants to the other students. This activity usually takes up very little class time, since the students already know how to edit and post webpages. There are about half a dozen HTML tags they need, and then they are directed to the many sources of HTML information on the Web. The usual assignment for this part of the course is for the students to make a moderately interesting web page. The page should say something about them, and it should also contain a link to some interesting mathematical item on the Web. (We always get links to the Math Forum and to some part of the MAA web pages). A second pass through the webpage creation phase gives students the opportunity to add background and foreground images to their pages.

The other Phase II activity involves studying the source code for some of the games that we played in Phase I and at the code for the several calculators that we used for our mathematical work in the course. We often spend half an hour in each of several classes discussing in general terms how a few of these pages work, so that students get an idea of how programs are conceptualized and then actualized. The game programs were mentioned in the Section 2. Some of the calculators are

• the long division calculator, which gives the quotient and remainder for integer division, and which is used in conjunction with the Euclidean algorithm,
• the prime factorization calculator, which we use in the number theory thread, and
• the statistical calculator.

Phase III. Beginning to program in Javascript

By Phase III, the students are ready to begin to program, more or less as they had begun in Phase IB to write webpages. In particular, students learned how to make buttons in HTML and to use short Javascript statements to make the buttons active.

The first part of this activity involves modifying an already-existing program, just as with the HTML tables at the beginning of the semester. In particular, students take a very simple page that has only one button (to add two numbers together), and modify it to make a "four-function calculator." The students experience and learn to deal with syntax and other errors, but almost all of them are able to complete this part on their own.

The second half of Phase III is more challenging. Students are required to generate a working program almost "from scratch". We begin with a general discussion of algorithms, in which we review all the games the students played earlier in the semester. We pay special attention to the level of specificity that will be required to communicate our intentions to the computer via a programming language -- any programming language!.

The first programming project that we undertake together is to calculate which day of the year a specific date falls on (e.g., February 5 is the 36^th day of the year). The Javascript webpage helps students get started with this one. Subsequent assignments are to calculate and display the number of days between two dates, or (more challenging!) the day of the week of a given date. In this phase, since the problems are chosen to have specific, concise answers, the programming for the output is fairly simple. In fact, we limit the output of the programs in this stage to simple "alert boxes" in which the answer is reported.

A student project based on this much of the programming experience, together with the exponential function unit of the course, is the Carbon-14 dating calculator. For the group of students who did it, this was a fairly ambitious undertaking, and they had to learn a little about the "Math" object in Javascript -- enough to use the exponential, logarithm and rounding functions.

Phase IV: Output, random numbers, iterations, and simulations

Toward the end of the course, students begin to learn how to manipulate data in Javascript and to rewrite the webpage in order to display the results of their calculations. This is difficult for some students, while others get completely involved in trying to outdo one another with fancy output or programs that are browser-independent. A couple of fun examples of student-produced programs are Get an A (wich works only under Internet Explorer) and the Light Switch Game. Both of these are examples of using and manipulating tables of images.

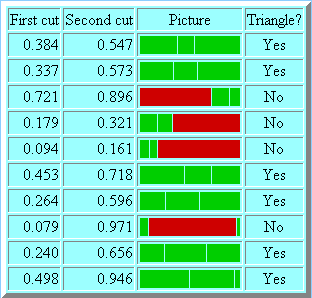In a more mathematical vein, we used our programming ability and Javascript’s random number generator to produce simulations and to display the results of iteration schemes. One of our simulations shows what happens when a stick is broken into three pieces by choosing two spots along the stick at random to cut it. The question is whether the three pieces can be assembled into a triangle -- so the criterion is that none of the three pieces should be more than half as long as the original stick. It is a nice problem to calculate the probability that the pieces can be so assembled, and the webpage contains a simulation of this, where the experiment is repeated in bunches of ten tries each, and the results are accumulated. An interesting variation on this problem is to cut the stick once at a random spot, and then cut the larger piece at a random spot along it.

Another simulation -- in response to a student question -- was to see why you divide by n - 1 instead of by n when you calculate the variance of a sample in statistics. To do this, we considered the experiment of flipping a coin over and over, getting one point for each head, and losing a point for each tail. Of course, the theoretical mean is zero points, and the standard deviation (in fact, every deviation) from the mean is 1. By taking modest-sized samples we could see that we got a better estimate of the theoretical variance by dividing by n  - 1.

Finally, one of the mathematics units we studied concerned iteration schemes for solving equations. The students discovered Newton’s method for calculating nth roots by experimenting, and eventually we looked at some examples of chaotic dynamics and fractals.

This article illustrates the use of web programming in HTML and Javascript both to enliven a liberal arts mathematics course and to illustrate and exemplify mathematical thinking. Students’ reactions to doing this have generally been positive. Those who already knew something (even a lot) about web programming usually learn something from our look at various aspects of composing and writing programs. And even though many of those who had never tried programming of any kind cannot complete all of the programming assignments on their own, getting a glimpse of how these things "really work" is often their favorite part of the course. My favorite comment was an e-mail in which a student remarked, "One of my friends has been taking a web programming course, and I am always showing him how to do things!"