Andrew G. Bennett is in the Department of Mathematics at Kansas State University. He is also an Associate Editor of this journal.

Hyperbolic geometry is a geometry for which we accept the first four axioms of Euclidean geometry but negate the fifth postulate, i.e., we assume that there exists a line and a point not on the line with at least two parallels to the given line passing through the given point. This corresponds to doing geometry on a surface of constant negative curvature. Such a geometry is very different from the familiar Euclidean geometry. This module has three applets designed to get you familiar with some of the basic properties of the hyperbolic plane.

The Poincaré half-plane model

Unfortunately, the hyperbolic plane can't be embedded in Euclidean 3-space. In order to represent the hyperbolic plane on a computer monitor, we must flatten out the curvature. In so doing, many of the straight lines in hyperbolic space become curved. One of the standard models of flattening out the hyperbolic plane is due to the French mathematician Henri Poincaré. In this model, the hyperbolic plane is squashed onto a Euclidean half-plane. The following links will take you to discussions of different features of this model. The discussions will make more sense if you view them in order.

Published July, 2001

© 2001 by Andrew G. Bennett

 

In the Poincaré half-plane model, the hyperbolic plane is flattened into a Euclidean half-plane. As part of the flattening, many of the lines in the hyperbolic plane appear curved in the model. Lines in the hyperbolic plane will appear either as lines perpendicular to the edge of the half-plane or as circles whose centers lie on the edge of the half-plane. Note that the edge of the half-plane itself (marked in gray in the picture) is not part of the hyperbolic plane.

With these definitions it is not hard to show that two points determine a line, as is required by Euclid's Axiom 1. It may initially appear that the second axiom, that any segment can be extended indefinitely, is violated by the existence of the edge. The trick is that distance is defined so that the edge is infinitely far away. To review the definition of distance, click here.

The applet

To help get you familiar with hyperbolic lines and distances, I've prepared an applet to let you experiment with them. You will need a Java-enabled browser to run the applet (Netscape 3.0 or higher or Internet Explorer 3.0 or higher on either Windows 95 or a Mac). Once you've read the following instructions, click the link below to launch the applet in a new window. If the resolution of your monitor is 640x480, you will probably want to maximize the window. If the resolution of your monitor is 800x600 or larger, you should see everything just fine the way it comes up on its own.

In the applet you will have two red points and two blue points, with each pair of points defining a hyperbolic line. Click your mouse on a point and drag it (while holding the mouse button down) to move the point. The line will follow the point. Off the edge of the half-plane (marked in gray), you will see the hyperbolic distances between the red points and between the blue points. You will also see a note about whether the lines are parallel. (Bug warning: Sometimes when the window is covered and then uncovered by other windows on your computer monitor the applet doesn't redraw itself completely. If you click on a point and move it, or if you minimize and then restore the window, the applet will redraw itself properly.)

Things to try

• Check that if you leave the red line fixed and one blue point fixed, there really are infinitely many lines through the fixed blue point that are parallel to the red line.
• Observe that distances are larger as you go down toward the edge than as you go up away from the edge. Since the points are shown with width and height (so you can click on them with your mouse), you can't push them all the way to the edge, so you can't actually push them infinitely far apart. (The point represented by each square is at the center of the square drawn on the screen.)
• Push the two squares as far apart as they will go on the screen, as measured by hyperbolic distance. Where are they farthest apart? (Hint: the farthest apart you can push them is over 90 units apart).

Click here to launch applet. (It will open a new window.)

 

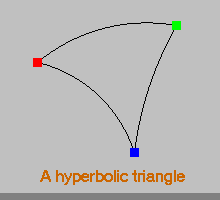The Poincare half-plane model is conformal, which means that hyperbolic angles in the Poincare half-plane model are exactly the same as the Euclidean angles -- with the angles between two intersecting circles being the angle between their tangent lines at the point of intersection. A hyperbolic triangle is just three points connected by (hyperbolic) line segments. Despite all these similarities, hyperbolic triangles are quite different from Euclidean triangles.

Since the hyperbolic line segments are (usually) curved, the angles of a hyperbolic triangle add up to strictly less than 180 degrees. Since a quadrilateral can always be cut into two triangles, a quadrilateral must have its angles add up to less than 360 degrees, so in hyperbolic geometry there are no squares, which makes defining area in terms of square units difficult. It turns out, however, that there is a unique function (up to multiplication by a scale factor) that satisfies the usual area axioms:

• Area is non-negative.
• If you cut up a figure into a finite number of pieces and rearrange them to form a second figure, then the two figures must have the same area.

For a triangle, this function is the defect, defined as

where the angles alpha, beta, and gamma are measured in radians.

In addition to the smaller angle sum, there are two other major differences between hyperbolic triangles and Euclidean triangles:

• While the sides of hyperbolic triangles can get as large as you want, the area of any triangle is less than pi.
• There is no concept of similar triangles -- if two triangles have the same angles then they are congruent. (They may look different in the model, since lengths appear different depending on how close they are to the edge, and that goes for area too.)

The applet

To help get you familiar with hyperbolic triangles, I've prepared an applet to let you experiment with them. You will need a Java-enabled browser to run the applet (Netscape 3.0 or higher or Internet Explorer 3.0 or higher on either Windows 95 or a Mac). Once you've read the following instructions, click the link below to launch the applet in a new window. If the resolution of your monitor is 640x480, you will probably want to maximize the window. If the resolution of your monitor is 800x600 or larger, you should see everything just fine the way it comes up on its own.

In the applet you will have a red point, a blue point, and a black point. The points are connected by (hyperbolic) line segments to make a triangle. The angles of the triangle are listed below the edge of the half-plane. They are color coded, so the angle at the red point is given in red, etc. Below these angles are the sum of the three angles and the area of the triangle. Click your mouse on a point and drag it (while holding the mouse button down) to move the point. The triangle will follow the point as in the other applets. (Bug warning: Sometimes when the window is covered and then uncovered by other windows on your computer monitor the applet doesn't redraw itself completely. If you click on a point and move it, or if you minimize and then restore the window, the applet will redraw itself properly again.)

Things to try

• Move the points around to check how the angle sums behave. Observe that the smaller the triangle, the closer the sum of the angles is to 180 degrees.
• What is the biggest area you can make in this applet? Since the points are shown with width and height so you can click on them with your mouse, you can't push them out to infinity, but you can get them far enough apart to get an area over 3. Where do you move the points to get the biggest area?
• What is the smallest angle sum you can make in this model. As above, you won't be able to reach the theoretical minimum, but you can get reasonably close.

Click here to launch applet. (It will open a new window.)

 

A circle in the hyperbolic plane is the locus of all points a fixed distance from the center, just as in the Euclidean plane. Therefore, the hyperbolic plane still satisfies Euclid's third axiom. A hyperbolic circle turns out to be a Euclidean circle after it is flattened out in the Poincare half-plane model. The only difference is that, since distances are larger nearer to the edge, the center of the hyperbolic circle is not the same as the Euclidean center, but is offset toward the edge of the half-plane.

Now that we know how to find linear distances and areas of triangles, we can find the circumference and area of a circle using the same trick as Archimedes, approximating the circle by inscribed and circumscribed n-gons and taking limits. As noted on the preceding page, there is no concept of similarity in hyperbolic geometry, and so it is not surprising that the formulas for hyperbolic circumference and area aren't simple proportions, as in the Euclidean case. In hyperbolic geometry

• Circumference = 2 pi sinh r
• Area = 4 pi sinh²(r/2)

where r is the radius of the circle.

The applet

To help get you familiar with hyperbolic circles, I've prepared an applet to let you experiment with them. You will need a Java-enabled browser to run the applet (Netscape 3.0 or higher or Internet Explorer 3.0 or higher on either Windows 95 or a Mac). Once you've read the following instructions, click the link below to launch the applet in a new window. If the resolution of your monitor is 640x480, you will probably want to maximize the window. If the resolution of your monitor is 800x600 or larger, you should see everything just fine the way it comes up on its own.

In the applet you will have a red point at the center of a circle and a blue point on the circle. The points are connected by a (hyperbolic) line segment, the radius, in red, and the (hyperbolic) circle itself is drawn in blue. Click your mouse on a point and drag it (while holding the mouse button down) to move the point. The radius and circle will follow the point. Off the edge of the half-plane (marked in gray), you will see the hyperbolic distance between the red point and the blue point. (Bug warning: Sometimes when the window is covered and then uncovered by other windows on your computer monitor the applet doesn't redraw itself completely. If you click on a point and move it, or if you minimize and then restore the window, the applet will redraw itself properly.)

Things to try

• How does the circumference of a hyperbolic circle of a given radius compare to the circumference of a Euclidean circle with the same radius? Does it make a difference if you compare big circles or little circles?
• How does the area of a hyperbolic circle of a given radius compare to the area of a Euclidean circle with the same radius? Does it make a difference if you compare big circles or little circles?
• How quickly do the circumference and area grow as the radius grows? How does this compare to the Euclidean case?
• Note that the circumference always exceeds the area for a hyperbolic circle. Can you prove this using the formulas given above? Does this happen for Euclidean circles? Could you make it happen for Euclidean circles if you used mixed units (e.g. measuring circumference in millimeters and area in square kilometers)?

Click here to launch applet. (It will open a new window.)