Parity Theorem for Permutations - Permutations and Transpositions
Permutations are bijective (one-to-one and onto) functions from a set to itself. When the set is {1, 2, …, n}, then its complete set of permutations is denoted by Sn, which is a group when composition of functions is taken as the operation.
A fundamental fact: Every permutation in Sn can be expressed as the composition of a sequence of transpositions.
A transposition is a very simple permutation that maps two distinct elements of the set to each other and everything else to itself. It can be represented by an ordered pair (a, b), where a and b denote the two elements that map to each other. This is clearly the simplest sort of permutation that there could possibly be, other than the identity permutation, which maps everything to itself.
It is easy to see why the claim in the preceding paragraph is true if one thinks of representing permutations in Sn by using n boxes numbered 1 through n and n similarly numbered markers. We may regard a distribution of the markers into the boxes, with one marker per box, as representing a permutation a in Sn. Specifically, we will think of such a distribution as telling us that a(i) = j when marker number i is to be found in box number j. For example, Figure 1 shows an arrangement of twelve numbered markers in twelve boxes. We will regard this arrangement of the markers as representing the permutation a such that a(1) = 12, a(2) = 5, a(3) = 8, etc.
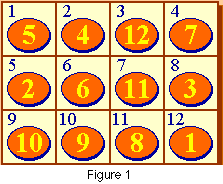
One could equally well reverse the roles of marker numbers and box numbers in terms of which represents the domain and which the range variables. The representation set forth here reflects a tactile point of view. We think of a function as going from the domain to the range. Thus, we are interpreting a(i) = j as saying that the marker that originally came from box i has gone to box j.
If we think about permutations in this way, then a transposition (a, b) is a permutation represented by the swapping of the contents of two boxes, namely box a and box b. If we compose a sequence of transpositions, then we can represent this by a sequence of steps of swapping pairs of markers between boxes. It does not take very long doing this, or even just thinking about it, before one sees clearly that one can achieve any permutation one wants by a sequence of swaps of markers. Equivalently, one can easily see how one could restore each marker to its home box in Figure 1 by doing a sequence of swaps.