Tool Building: Web-based Linear Algebra Modules
Getting students to interact with linear algebra content can be a daunting task, especially when you want them to recognize the algebraic and geometric meanings behind many of the concepts. We present a glimpse of the possible -- here is a student voice to introduce what we mean by "the possible":
"I learned alot [sic] through the use of Eigenizer & Gridmaster & Transformer. Although they were difficult to use at first, because I did not know what I was looking for, and could not see the connections, by the end of the year, eigenizer taught me basically all of the connections with eigenvalues, eigenvectors, character poly & so forth. At first, I did not understand and had trouble following class discussions about eigenvalues & so forth, but after doing the project, everything came together because I could visually see the connection. I know this is a specific example, but I think all of the programs were helpful to see the linear algebra concepts in the program."
David E. Meel and Thomas A. Hern are in the Department of Mathematics and Statistics at Bowling Green State University.
In no way do we claim to provide a final word on the subject, but we provide
-
several tools that are helpful for students when investigating difficult linear algebra concepts,
-
student reaction to these tools from classroom use, and
-
some technical details of how the tools were built.
Some of the tools produced to study and visualize linear algebra concepts are described by
-
the ATLAST project (Leon, Herman & Faulkenberry, 1996),
-
the special edition on linear algebra in the College Mathematics Journal edited by Ann and Bill Watkins (1993),
-
the MAA volumes, Resources for Teaching Linear Algebra (Carlson et al., 1997), and
-
Linear Algebra Gems (Carlson et al., 2002).
We have noticed in these sources a lack of stand-alone tools. For instance, the tools generated by the ATLAST project were designed as MATLAB applications, and others have been based on Mathematica, Maple, and other software systems. This usually requires the user to own or have access to a particular software product, which may not be available for all platforms. In addition, some basic skill in using the software is usually required.
We present in this paper several interactive web-based tools for visually exploring various linear algebra concepts, tools that are not constrained by the requirement of owning particular software. By building these tools with JavaSketchpad, the only requirement for a user is a Java-enabled browser. In particular, we present three tools, GridMaster, Transformer2D, and Eigenizer, and a couple of bonus items for advanced linear algebra.
Each figure below shows a small part of the JavaSketchpad window -- click on each image or its title to see a picture of the full window.
 |
 |
|
|
|
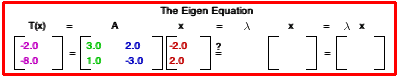
Each of these tools permits students to interact with both algebraic and geometric representations of concepts such as change of bases, coordinate systems, linear transformations, eigenvalues, and eigenvectors. We include student reactions to enhance the discussion and identify the effects of using such tools as part of linear algebra explorations.
Published May, 2005
© 2005 by David E. Meel and Thomas A. Hern
Tool Building: Web-based Linear Algebra Modules - Introduction
Getting students to interact with linear algebra content can be a daunting task, especially when you want them to recognize the algebraic and geometric meanings behind many of the concepts. We present a glimpse of the possible -- here is a student voice to introduce what we mean by "the possible":
"I learned alot [sic] through the use of Eigenizer & Gridmaster & Transformer. Although they were difficult to use at first, because I did not know what I was looking for, and could not see the connections, by the end of the year, eigenizer taught me basically all of the connections with eigenvalues, eigenvectors, character poly & so forth. At first, I did not understand and had trouble following class discussions about eigenvalues & so forth, but after doing the project, everything came together because I could visually see the connection. I know this is a specific example, but I think all of the programs were helpful to see the linear algebra concepts in the program."
David E. Meel and Thomas A. Hern are in the Department of Mathematics and Statistics at Bowling Green State University.
In no way do we claim to provide a final word on the subject, but we provide
-
several tools that are helpful for students when investigating difficult linear algebra concepts,
-
student reaction to these tools from classroom use, and
-
some technical details of how the tools were built.
Some of the tools produced to study and visualize linear algebra concepts are described by
-
the ATLAST project (Leon, Herman & Faulkenberry, 1996),
-
the special edition on linear algebra in the College Mathematics Journal edited by Ann and Bill Watkins (1993),
-
the MAA volumes, Resources for Teaching Linear Algebra (Carlson et al., 1997), and
-
Linear Algebra Gems (Carlson et al., 2002).
We have noticed in these sources a lack of stand-alone tools. For instance, the tools generated by the ATLAST project were designed as MATLAB applications, and others have been based on Mathematica, Maple, and other software systems. This usually requires the user to own or have access to a particular software product, which may not be available for all platforms. In addition, some basic skill in using the software is usually required.
We present in this paper several interactive web-based tools for visually exploring various linear algebra concepts, tools that are not constrained by the requirement of owning particular software. By building these tools with JavaSketchpad, the only requirement for a user is a Java-enabled browser. In particular, we present three tools, GridMaster, Transformer2D, and Eigenizer, and a couple of bonus items for advanced linear algebra.
Each figure below shows a small part of the JavaSketchpad window -- click on each image or its title to see a picture of the full window.
 |
 |
|
|
|
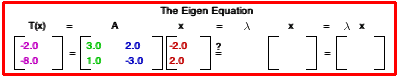
Each of these tools permits students to interact with both algebraic and geometric representations of concepts such as change of bases, coordinate systems, linear transformations, eigenvalues, and eigenvectors. We include student reactions to enhance the discussion and identify the effects of using such tools as part of linear algebra explorations.
Published May, 2005
© 2005 by David E. Meel and Thomas A. Hern
Tool Building: Web-based Linear Algebra Modules - Ways to Read this Article
Our initial aim is to demonstrate several web-based tools designed to explore elementary linear algebra content. We know that readers may have different interests, and this web-based environment allows you to navigate in different ways. We have developed the following three different paths through the article:
-
The Tool path, indicated by the icon
 :
:
This path considers only at the Tools and corresponding sample activities. Prior to linking to a tool, we provide a brief orientation to the elements of that tool. -
The Pedagogical path, indicated by the icon
 :
:
This path augments the Tool path with examples of student work and their reactions to the tools and cognitively guided activities. -
The Researcher path, indicated by the icon
 :
:
This path augments the Pedagogical path with discussions of student difficulties and research into ways to help students overcome cognitive obstacles.
You will be able to navigate to the next item on your selected path by page numbers stated at the bottom of each page. If you follow every page, you will be on the Researcher path. As you move between pages, you will stay in the same window, but each tool will open in a separate window, allowing you to explore while walking through the orientation, as well as attempt the sample activity.
Next ![]() or
or ![]() page: 4. GridMaster Tool and Sample Activity
page: 4. GridMaster Tool and Sample Activity
Next ![]() page: 3. Discussion of GridMaster
page: 3. Discussion of GridMaster
Tool Building: Web-based Linear Algebra Modules - Discussion of GridMaster
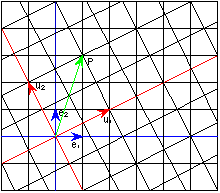
![]() In January of 2002, we discovered a paper entitled "Multigrid Graph Paper" (Bevis, 2002) that claimed multigrid paper (see Figure 1) would be helpful for students studying a variety of linear algebra concepts such as linear transformations, change of bases, and coordinate systems.
In January of 2002, we discovered a paper entitled "Multigrid Graph Paper" (Bevis, 2002) that claimed multigrid paper (see Figure 1) would be helpful for students studying a variety of linear algebra concepts such as linear transformations, change of bases, and coordinate systems.
|
|
Figure 1. Multigrid paper |
In Figure 1 we can see that vector P has coordinates [1,3] with respect to the natural basis {e1, e2}, but with respect to {u1, u2}, the vector P has coordinates [1,1].
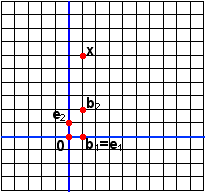
We saw the multigrid paper as a means of streamlining the Lay (2003) presentation of coordinate systems using two different graph papers. In particular, Lay (2003) described the use of two separate grids similar to those shown in Figures 2 and 3 when negotiating between two coordinate systems. For instance, the vector x has coordinates 1 and 6, typically expressed as ![]() with respect to the natural basis {e1, e2} (see Figure 2). In contrast, Figure 3 displays the vectors b1, b2 and x, but in reference to a grid defined by b1 and b2. The position of x has not moved, but
with respect to the natural basis {e1, e2} (see Figure 2). In contrast, Figure 3 displays the vectors b1, b2 and x, but in reference to a grid defined by b1 and b2. The position of x has not moved, but ![]() .
.
 |
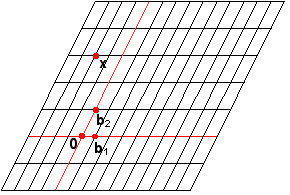 |
Figure 2. Standard graph paper |
Figure 3. B-graph paper |
After examining Bevis' article, which suggested overlaying multiple grids on a single sheet, we felt that static multigrid graph paper could be improved upon by using The Geometer's Sketchpad. The resultant web-based module, entitled GridMaster, permits students to model a portion of R2 and define vectors that coordinatize this vector space. Specifically, this first module was designed to help students recognize the meanings of different coordinate systems and change of bases, two topics identified as difficult for students to understand (Carlson, 1993).
In addition, we sought to address an observation of Hillel (2000) that some of the representations used in linear algebra can serve as obstacles to the development of student understanding. Hillel specifically identified that students have difficulty generalizing the notion of an n-tuple as no longer representing a single vector but a potential representation of any other vector. This is of significant importance when students have to work across different bases. This observation motivated us to look for different ways, other than the purely computational MATLAB interactions we had used before, to cause students to interact with multiple representations simultaneously.
Next ![]() or
or ![]() or
or ![]() page: 4. GridMaster Tool and Sample Activity
page: 4. GridMaster Tool and Sample Activity
Tool Building: Web-based Linear Algebra Modules - GridMaster Tool and Sample Activity
| |
| |
| |
You will want to open the GridMaster web page in order to understand the following discussion. (Note: It will take a while to download JavaSketchpad initially, so please be patient.)
Open GridMaster in new window
You can use GridMaster to construct electronic multigrid paper. Start by moving the green and blue vectors -- click on a circle at the end of a vector and drag it to a new position. Then click on the appropriate button to display a grid, e.g., a green grid corresponding to the green vectors. You can resize the scale of the entire grid space by moving the point e(1) if you need more a larger or smaller range of values. In the upper left, you will see the coordinates of the point P (the red vector) with respect to the natural basis and then with respect to the bases [P]B defined by the blue vectors and [P]Gdefined by the green vectors.
Note: The "?" at the bottom right-hand corner of the workspace is a link to Key Curriculum Press and its About JavaSketchpad web page.
Sample Exploratory Activity:
Find the vector P determined by the given coordinate vector [P](u,v) and the given basis {u,v}.
 ,
, 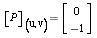
 ,
, 
Given the vector P and a basis {u,v}, find the coordinate vector [P](u,v).
 ,
, 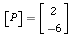
 ,
, 
Use the information provided to determine the missing element.
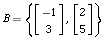 ,
,  , and
, and  . Find
. Find 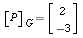 .
.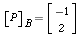 ,
, 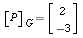 , and
, and 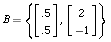 . Without attempting to coordinatize P with respect to the standard basis, find a basis G that satisfies these conditions, if any exists.
. Without attempting to coordinatize P with respect to the standard basis, find a basis G that satisfies these conditions, if any exists.
This last question begins to motivate a need to construct a change-of-coordinates matrix in order to determine more readily if a solution exists. Although there are an infinite number of solutions, determining a single one using GridMaster requires careful attention to the interaction of vectors and how they impact the movement of the grid lines and values of the coordinatized vectors.
Next ![]() or
or ![]() page: 6. Transformer2D Tool and Sample Activity
page: 6. Transformer2D Tool and Sample Activity
Next ![]() page: 5. Discussion of Transformer2D Tool
page: 5. Discussion of Transformer2D Tool
Tool Building: Web-based Linear Algebra Modules - Discussion of Transformer2D
![]() When students look at a matrix of transformation, at best they examine it as the coefficient matrix of a system of linear equations, and at worst they consider it a random array of numbers completely devoid of meaning. In addition, when we as teachers describe a matrix, we often read the elements row-by-row, further separating the potential geometric considerations of column vectors. Consequently, students have a difficult time when faced with geometrically interpreting matrices of transformations other than simple ones involving positive and negative ones and zeros. In response, we began to search for a means to help students interact with matrices of transformations that would lead them to viewing the column vectors as having powerful information.
When students look at a matrix of transformation, at best they examine it as the coefficient matrix of a system of linear equations, and at worst they consider it a random array of numbers completely devoid of meaning. In addition, when we as teachers describe a matrix, we often read the elements row-by-row, further separating the potential geometric considerations of column vectors. Consequently, students have a difficult time when faced with geometrically interpreting matrices of transformations other than simple ones involving positive and negative ones and zeros. In response, we began to search for a means to help students interact with matrices of transformations that would lead them to viewing the column vectors as having powerful information.
Our use of Sketchpad for investigation of linear transformations from R2 to R2 allows students to investigate the geometry underlying linear transformations as well as to grapple with the way vector spaces are mapped into other vector spaces. Getting students interested, exploring, and excited can lead them to making deep insights into the content and is one of the primary goals of these web-based tools. As students investigate a large number of examples in a short period of time, they are forced to revise their conjectures over and over again until settling upon insights that are compatible with mathematical definitions of the concepts.
Consequently, we designed the Transformer2D tool to get students to interact with the concept of linear transformation that acts as a "unifying and generalizing concept" permeating the whole of linear algebra (Dorier 1991, 1995; Dorier et al. 2000a, 2000b). A perspective on the geometric meaning of the column vectors in a matrix of transformation can potentially help students overcome some of their difficulties, as identified by Carlson (1993) and Meel (1999b), with related concepts such as null and column spaces.
We developed this tool over an extended period of time. During the Spring 2002 and Fall 2003 terms, we pilot-tested the web-based tools to determine students' reactions to them and to test the transparency of the interface. Based on findings from a beta version written in The Geometer's Sketchpad 3.0 (Jackiw, 1995), elements of the module were not sufficiently transparent. Students were frustrated that particular elements could be moved which should have been held static. This and other observations gave rise to our developing the web-based modules that could lock elements of the sketch. In addition, moving to web-based modules allowed students to access the modules remotely without having to own Geometer's Sketchpad. During pilot testing of Transformer2D we found that students needed a primer on how to interact with the interface and displayed difficulties with interpreting the information they were receiving from the module. For instance, one student stated:
"I found the programs very difficult to understand. I do not learn well by computers, but I do think they are a good way to visualize the problem. They helped me see what was going on. . . . I think in the future it would be helpful to hand out a ditto explaining the programs, so that students can become familiar with all the features the program has to offer."
Another student said:
"The most difficult/frustrating thing of working with the programs was not knowing what I was looking for, and making connections and discovering things on my own. However, this turned into the best thing at the end because it is a good feeling once you make the connection."
As a consequence, we present in this article the revised interface that is accompanied by a more thorough explanation of the role of particular buttons and features.
Next ![]() or
or ![]() or
or ![]() page: 6. Transformer2D Tool and Sample Activity
page: 6. Transformer2D Tool and Sample Activity
Tool Building: Web-based Linear Algebra Modules - Transformer2D Tool and Sample Activity
| |
| |
| |
Using Transformer2D is considerably different from using GridMaster, in which all actions took place on a single graphical interface. In Transformer2D, the interface has been partitioned into different regions, each having its own purpose. The yellow box (upper left) controls the column vectors defining the matrix of transformation -- the green vector is the first column and the blue vector is the second column. By grabbing and moving the ends of these two vectors, you can construct any 2x2 matrix. Clearly, varying the matrices' column vectors changes only the matrix. This encourages students to think about Ax as a linear combination of the columns of A and hopefully begin to recognize that the column space is the range of the transformation.
Below the yellow box is a box that controls the vector x. As you move x (the red vector) about the domain of the transformation, you can watch the image T(x) (the magenta vector) change in the large area to the right of the screen depicting the codomain. Partitioning the sketch in this way allows students to investigate separately the impact of changes to the matrix of transformation and of the value of the x-vector. However, in order not to focus solely on the transformation of a single vector, we have provided a variety of other built-in graphical elements in the domain: a unit circle, a unit square, a unit grid, and an adjustable quadrilateral. (Change the shape of the quadrilateral by moving its vertices.) Students can view the transformations of each of these shapes by selecting the corresponding button in the domain sector. In addition, students can turn on or off a tracing feature that marks out the path of the transformed vector T(x) as x is varied. This feature allows students to carry out freehand investigations.
Open Transformer2D in new window
Warning : The Transformer2D page is best viewed in 1024 x 768 resolution or greater and may take up to a minute to load.
Notes:
-
You can clear the traces whenever you want by clicking on the X that appears in the lower right hand corner.
-
The "?" also at the bottom right-hand corner of the workspace is a link to Key Curriculum Press and its About JavaSketchpad web page.
Sample Exploratory Activity:
This sample activity provides a guided exploration of a particular matrix of transformation and includes a set of questions that can be asked for any other matrix of transformation.
- Using the vectors contained in the yellow box, move (by click-dragging) the green vector to (3,-1) and the blue vector to (-2,2). This should construct the following matrix of transformation:
 .
. - In the domain box, click on Show UNIT circle, and use the red vector x to trace around the unit circle by clicking and dragging. Be sure to observe happening in the box to the right with the magenta vector labeled T(x).
- To get a better view of what T(x) traces out, click on the Turn Trace ON button and repeat the previous step.
- Use the Transformed UNIT circle button to reveal the exact transformation of the unit circle under the matrix of transformation. (The image can be hidden by using the Hide UNIT circle button.)
- When you have finished exploring the unit circle, click on Hide UNIT circle , click on X to clear the traces, and click on Turn Trace OFF.
- Select another geometric shape to be revealed in the domain of the transformation box by clicking on the appropriate button. Repeat the above explorations for all the different geometric shapes available, since each reveals a different piece of what the matrix of transformation does.
Given your exploration, answer the following questions:
- Describe what happens to the unit circle under the transformation.
- Describe what happens to the unit square under the transformation.
- Describe what happens to the unit grid under the transformation.
- Describe what happens to the quad under the transformation.
- Describe in general what happens to any element of the domain under the transformation, i.e. what does its image look like in the codomain? Is it stretched, shrunk, rotated, etc.?
In addition, Transformer2D can be used to find a matrix of transformation with particular properties such as:
- Find a matrix of transformation that rotates geometric figures 180º and doubles their size. (Note: The imprecise language here is deliberate to get students to start thinking that definitions are important and can impact their eventual proposed offerings.)
- Find a matrix of transformation that transforms turns all geometric shapes into a line or a segment of that line.
Next
Next ![]() or
or ![]() page: 7. Student Responses, Part 1
page: 7. Student Responses, Part 1
Tool Building: Web-based Linear Algebra Modules - Student Responses, Part 1
| |
| |
- "Scaling a vector v while leaving u alone expands the unit grid in the direction of v, makes the unit square a rectangle, and alters the unit circles diameter to make it an oval with the long dimention [sic] parallel with v."
- "The shape of the transformation of unit circle is dependent on u & v and not on x."
- "Making the vectors u and v scalars of one another makes a scalar of T(x) and changes the length and direction of by moving the domain of the transformation."
- "If the vectors are the same length but opposite directions -- T(x) is at the center."
- "Rotating u, rotates the quad about the v vector."
- "As long as the vectors are not colinear [sic], we can map to any place in R2."
- "The direction of x does not directly effect [sic] the direction of T(x). We now observe that after changing u and v, x does effect [sic] the direction of T(x)."
Each of these comments provides evidence of how students interact with the concept of linear transformations in manners atypical of classroom discussion. Even though some of the statements may reveal misinterpretations and mis-generalizations, the overarching goal of the tool is to help students experience the mathematics and then lead them to examine additional examples that help them recognize the misinterpretation or mis-generalization. For instance, the last comment came from a pair of students who at first examined a particular example and made a particular observation. Then, after changing the values of u and v, they noticed that the previous observation was incorrect and they adjusted their observation. Getting students to interact directly with the linear algebra concepts allows them to formulate conjectures and then test them.
For example, one student wrote in his e-mail dialogue journal:
"I have been working on the problems presented in the transformer worksheet and had a breakthrough. I think I understand how the transformations effect [sic] the vectors. The unit grid portion of the program is very useful. I think I understand a little better how the signs in different areas change the grid and the different values of vectors affect the transformation."
Another student wrote,
"The project you had us do was very helpful. I learned a lot about transformations when you asked us to explain what was going on without knowing what a transformation was. Now if I were to go back and explain what was going on in each matrix, I would use terms like, reflection, contractions and expansions, shears (vertical and horizontal) and projections. When using the unit circle or unit square, you can see what each matrix does to it and therefore you can conclude some sort of transformation."
To get a better feel for how students interacted with the Transformer2D tool and its correspondent cognitively-guided activity, we show on the next page a sample student response to the entire activity.
Next
Next ![]() or
or ![]() page: 8. Student Responses, Part 2
page: 8. Student Responses, Part 2
Tool Building: Web-based Linear Algebra Modules - Student Responses, Part 2
The Work of Jack
| |
| |
Our purpose for the Transformer activity is to get students to explore, make conjectures, and adjust their conjectures. To give a sense of how students use Transformer2D, we provide the work of a randomly selected student named Jack.
The worksheet link on the preceding page downloads a one-page MS Word document with the full statement of the project. However, students were working with a multi-page version with space to fill in their answers. We provide that version here as a PDF file.
Here are the parts of Jack's work as scanned images -- each opens in a separate window, and you may want to have more than one open at a time.
It is evident from Jack's work that he has a growing need for language to describe the phenomena he is encountering. Terms such as "shear," "reflected," and "rotated" are being drawn from the text to help explain the changes he observes in the geometric figures. As a consequence of this type of encounter, students come to appreciate the discussion of the terms and their meanings because they have a need for precise definitions of what they are experiencing.
Jack's described his reactions to the transformer project in his weekly journal entry:
"In class this week we started looking at transformation matrices, still in the form Ax = b. Now this is the same equation we have been using, but now we are looking at it in a different way. Going into the computer lab we started a project using the transformer on Dr. Meel's personal website. This was an interesting tool, because it allowed us to see the effects of different matrices on the range of values in R^2. The different kinds of transformations include reflections, contractions, expansions, vertical and horizontal shear, and projection onto the x-axis and y-axis.
"The project at first seemed a little overwhelming to be honest. I really had no clue how to tell what each matrix was doing by looking at them. But as I tried more and more matrices, and experimented to see what changes I made would create, it all started to make sense. After messing around for a while with the transformer and reading the book, I was able to go through the packet and do my best to answer the questions. Some of them I am not entirely sure I approached the correct way, but I am sure that I understand transformations a lot better in spite of that. So even if I am slightly off from the answers, I at least have an understanding of what transformations are and how to create some myself."
We are immersing students in a learning situation in which making sense of the environment is one major component as they grapple with their own limited perspectives and enhance their understandings of one or another concept piece by piece. In such an environment, they keep exploring, keep conjecturing, keep trying to organize thinking in new ways to accommodate the new bits of information being displayed, while at times experiencing considerable frustration because they lack the big picture. The tools and the corresponding projects are designed to eliminate the frustration and also to permit the teacher to assist, probe for understanding, point out significant hurdles, suggest alternative lines of thinking, and help equip students to manage their frustration and continue to pursue knowledge.
Next ![]() or
or ![]() page: 10. Eigenizer Tool and Sample Activity
page: 10. Eigenizer Tool and Sample Activity
Next ![]() page: 9. Discussion of Eigenizer Tool
page: 9. Discussion of Eigenizer Tool
Tool Building: Web-based Linear Algebra Modules - Discussion of Eigenizer Tool
![]() Many students claim to have difficulty understanding the concepts of eigenvalues and eigenvectors (Meel, 1999b). One possible explanation for this difficulty could be that students typically associate eigenvalues and eigenvectors with a computational process and do not understand the geometric connections.
Many students claim to have difficulty understanding the concepts of eigenvalues and eigenvectors (Meel, 1999b). One possible explanation for this difficulty could be that students typically associate eigenvalues and eigenvectors with a computational process and do not understand the geometric connections.
So, how do we encourage students to begin to look beyond the computations and consider the geometry? We consider an associated cognitively-guided activity as the means of forcing students to come to grips with both the computational process and the underlying geometric relationship between eigenvalues and eigenvectors. Specifically, the activity integrates the capabilities of MATLAB (MATLAB, 1995) with the Eigenizer tool. By blending the 2D graphical examination of eigenvalues and eigenvectors through the Eigenizer tool with examination of higher dimensional eigenspaces through MATLAB, we lead students to explore eigenvalues and eigenvectors from multiple perspectives.
This experience stimulated one student to make the following comment:
I liked working with eigenizer and MATLAB simultaneously. That way, I could see what it would look like with l = 0 and l = a+bi. Also the eigenizer showed why an eigenvalue was (+) or (-) depending on which way the vectors pointed."
Another student stated
"I learned the most from the eigenizer project. The eigenizer helped you see that the formula was true, but you need to do the work in order to find all of the eigenvalues, not rely solely on the computer. Eigenizer needs to be able to do (3) vectors."
Looking at the Eigenizer tool and its cognitively-guided activity as a whole, we see that students are being asked to look beyond the computations and understand the meanings behind the concepts eigenvalue, eigenvector, and eigenspace.
Next ![]() or
or ![]() or
or ![]() page: 10. Eigenizer Tool and Sample Activity
page: 10. Eigenizer Tool and Sample Activity
Tool Building: Web-based Linear Algebra Modules - Eigenizer Tool and Sample Activity
| |
| |
| |
Working with Eigenizer, similar to Transformer2D, involves coordinated actions between defining the column vectors of the matrix of transformation. The yellow box controls the column vectors defining the matrix of transformation. In particular, the green vector controls the first column vector and the blue vector controls the second column vector. By grabbing the ends of these two vectors, you can construct any 2x2 matrix.
Below the yellow box is a box that controls the vector x. As you move x (the red vector) about the domain of the transformation, you can watch both x and the image T(x) (the magenta vector) change in the large area to the right of the screen, depicting the codomain of the transformation. The movement of the vector T(x) depends on the nature of the matrix of transformation.
The large codomain region also displays information concerning the length of the vector x, the length of the vector T(x), the radian measure of the angle between these two vectors, and a lambda approximator. Two buttons at the bottom of this region control the display of the Eigen Equations in a red box above the codomain box.
Open Eigenizer in new window
Note: The "?" at the bottom right-hand corner of the workspace is a link to Key Curriculum Press and its About JavaSketchpad web page.
Sample Exploratory Activity:
This sample activity provides a guided exploration of eigenvalues and eigenvectors of a particular matrix and includes a set of questions that can be asked for any other matrix, as well as some general questions about the tool and observations made from interacting with the tool.
- Using the vectors contained in the yellow box, move (by click dragging) the green vector to (3,-1) and the blue vector to (-2,2). This should construct the following matrix of transformation:
 .
. - Move the red vector x (in the domain portion of the tool) and observe the movement of the magenta vector, T(x). If possible, move the vector x so that the vectors T(x) and x are collinear. Note: This can be aided by examining the angle measure at the bottom of the y-axis in the range portion of the tool.
- Click on the "Show lambda 1 equation" button, and observe whether the equation is true, i.e., do the vectors displayed on the right and left sides of the equation match each other? If they do not match, click on the "Show lambda 2 equation" button, and check if truth is found.
- Move the red vector x (in the domain portion of the tool) so that it and the T(x) vector are collinear in a different location.
- Redo step 3 for this new location.
Given your exploration (and perhaps some additional ones), answer the following questions:
- What are the eigenvalues for this matrix?
- What are corresponding eigenvectors for these eigenvalues?
- What does the lambda approximator do?
- If an eigenvalue is positive, what does this mean concerning the form of collinearity between the vector x and the vector T(x)? If an eigenvalue is negative, what does this mean concerning the form of collinearlity between the vector x and the vector T(x)?
- Can you have a matrix with two positive eigenvalues or two negative eigenvalues? Explain why or why not
- For a given eigenvalue, is there a unique eigenvector or a set of corresponding eigenvectors? If unique, explain why it's unique and if there is a set, explain how to describe the set.
- Define a matrix that does not have any real eigenvalues? In general, what would be the nature of the column vectors of such a matrix?
- Is it possible to define a matrix that has eigenvalues of -3 and 2? If it is possible, state how many such matrices could be constructed, and provide a specific example of at least one.
- Is it possible to define a matrix that has only a single eigenvalue, say -2? Explain why or why not.
The tool allows students to explore specific matrices as well as hypothesize about possible matrices with particular properties. It is with the latter type of explorations that the worlds of geometry and computation can fuse. Students need to think beyond computations that MatLab might be able to perform and ponder the possibilities of "what if?".
Next
Next ![]() or
or ![]() page: 11. Student Responses
page: 11. Student Responses
Tool Building: Web-based Linear Algebra Modules - Student Responses
| |
| |
- "An eigenvalue when multiplied by an eigenvector yields the same result as when matrix A is multipled [sic] by the eigenvector. Thus matrix A acts like the scalar eigenvalue".
- "An eigenvalue is a value that lets the matrix act like a scalar. An eigenvector is a nonzero vector that corresponds to the eigenvalue, if Ax = the eigenvalue * x".
- "The eigenvector is multiplied by A to make A act like a scalar. The eigenvalue of the vector is the lambda that A acts as when the vector is multiplied by it".
- "An eigenvalue of a matrix A is a scalar that when multiplied with a vector x yields the same resultant vector as A*x. An eigenvector of a matrix A is a vector that when multiplied with a scalar lambda yields the same resultant vector as when multiplied with the matrix A".
- "In our words, an eigenvalue is a way of representing a matrix as a scalar. This will allow the investigation of a matrix of transformation (T) on a vector (T(x)) without complicated calculations. The eigenvector provides a relationship between the values of x for which the lines are co-linear [sic]".
- "An eigenvalue, with it's eigenvector, 'mimic' A when multiplied together. Meaning, A acts like a scalar when multiplied with the eigenvector. Since lambda is derived by solving det(A - lambda In)x = 0, it 'unravels' to Ax = lambda x, which is what I described above".
- "The eigenvalues are related to A in that when multiplied by the In matrix and subtracted from A, you can row reduce to find a basis to the corresponding R space. The corresponding eigenvectors form the basis that spans the R space".
Clearly, some of the students were able to make observations that were generally consistent with mathematical definitions of eigenvalue and eigenvector and others made remarks that were slightly askew from such definitions.
However, being able to explore the geometry associated with eigenvectors and eigenvalues allowed some students to identify that MATLAB provided anomalous results when they encountered the following problem (2c in the accompanying activity):
- Using Eigenizer, determine how many times the vectors x and Ax are collinear? When the vectors x and Ax are collinear, what is the significance of the value of the eigenvalue in relation to the direction of an eigenvector of A, x, and its image T(x)?
- How many eigenvalues does A have? Are they real or nonexistent? Are they distinct or multiple? How many are positive? negative? zero? Is A invertible? Explain.
- Obtain a rough estimate of an eigenvector for each eigenvalue and then reveal the rest of the eigenvalue equation by pressing one of the "Show lambda # equation" buttons. Is the eigenvalue equation a truth within reasonable error? Move the vector x so it is no longer an eigenvector. Is the new equation true? Is the set of eigenvectors linearly independent? Explain.
- Compute by hand or by using Matlab the characteristic polynomial, the exact eigenvalues, and exact eigenvectors. Compare your results to your estimates in part 3. If you use Matlab,
- v = poly(A) gives the coefficients of the characteristic polynomial of matrix A, starting with the highest-degree term.
- k = roots(v) gives the roots of the characteristic polynomial of A, or use eig(A) to accomplish the same thing.
- nulbasis(A-k(1)*eye(2)) and nulbasis(A-k(2)*eye(2)) will give the eigenvectors, where each k(i) is a particular eigenvalue of A.
- If a matrix produced non-existent eigenvalues, what did you determine about the eigenvalues from part 4 when you computed them by hand or via Matlab?
Here are some sample solutions provided by students for the 2c matrix:


Our other samples are in a separate page because of their width.
Better understanding of both the computational and geometric roles of eigenvalues and eigenvectors, when combined with enhanced understandings of change of bases and linear transformations, sets the stage for investigations into diagonalization and potentially Singular Value Decompositions. One of our goals in having students explore the geometric perspective associated with eigenvalues and eigenvectors is to get students to begin to recognize that computations cannot be taken at face value but need to be examined within context for validity.
Next ![]() or
or ![]() page: 14. Transformer3D Tool and Sample Activity
page: 14. Transformer3D Tool and Sample Activity
Next ![]() page: 12. What is JavaSketchpad?
page: 12. What is JavaSketchpad?
Tool Building: Web-based Linear Algebra Modules - What is [i]JavaSketchpad[/i]?
![]() What we have done here is use an existing software product, The Geometer's Sketchpad (Jackiw, 2001), but in a way for which it was not originally designed. It is intended for geometric constructions, but we have used the geometric basis and the interactivity to build our tools. Moreover, the current version has an applet, JavaSketchpad, which allows most Sketchpad code to be run on a Java-enabled web browser. So we now have true platform- and software-independence as well. The tools in this article download the JavaSketchpad applet and the accompanying code in a way that is transparent to the user. The only skill required is use of a web browser -- a nearly universal skill these days.
What we have done here is use an existing software product, The Geometer's Sketchpad (Jackiw, 2001), but in a way for which it was not originally designed. It is intended for geometric constructions, but we have used the geometric basis and the interactivity to build our tools. Moreover, the current version has an applet, JavaSketchpad, which allows most Sketchpad code to be run on a Java-enabled web browser. So we now have true platform- and software-independence as well. The tools in this article download the JavaSketchpad applet and the accompanying code in a way that is transparent to the user. The only skill required is use of a web browser -- a nearly universal skill these days.
According to Key Curriculum Press (2001, p. 231), "JavaSketchpad is a Sketchpad extension that allows you to place simple sketches inside web pages you publish on the Internet." This allows an Internet user to interact with the elements of the sketch by dragging points and pressing action buttons even if they do not have local access to Sketchpad. JavaSketchpad is a scaled-down version of Sketchpad and therefore not capable of all the constructions generally available through The Geometer's Sketchpad 4.01.
Two elements are necessary to build a JavaSketchpad in order to interact with the dynamic sketch. The first element is the HTML file that contains the descriptions necessary to render the web page, as well as the descriptions of the geometric construction and associated action buttons included in the sketch. The second element is the JavaSketchpad applet. This applet differs from that of a plug-in which must be installed by the user prior to operating a particular application. The applet is held in the same directory as the HTML file and is downloaded at the same time the HTML file is accessed from the visitor's machine. In particular, "The applet -- a separate set of files -- provides the functionality that interprets this description (of the geometric construction), displays the figure in your visitor's browsers, and lets them interact with it" (Key Curriculum Press, 2001, p. 232). This simplifies the transfer and allows the user to interact seamlessly with the sketch without having to first download and install a plug-in.
Next ![]() or
or ![]() page: 14. Transformer3D Tool and Sample Activity
page: 14. Transformer3D Tool and Sample Activity
Next ![]() page: 13. Overcoming JavaSketchpad's Limitations
page: 13. Overcoming JavaSketchpad's Limitations
Tool Building: Web-based Linear Algebra Modules - Overcoming [i]JavaSketchpad[/i]'s limitations
![]() Our construction of each tool required some additional work beyond the development via a Sketchpad 4.01 document. Due to JavaSketchpad's limited command structure, particular constructions available in Sketchpad were not replicable in JavaSketchpad. For instance, when attempting to use the coordinates of a point as part of a computation, JavaSketchpad would permit one to obtain the coordinates but would not separate the abscissa and ordinate. Consequently, we used trigonometric relationships and relating lengths to the unit length to compute the needed values.
Our construction of each tool required some additional work beyond the development via a Sketchpad 4.01 document. Due to JavaSketchpad's limited command structure, particular constructions available in Sketchpad were not replicable in JavaSketchpad. For instance, when attempting to use the coordinates of a point as part of a computation, JavaSketchpad would permit one to obtain the coordinates but would not separate the abscissa and ordinate. Consequently, we used trigonometric relationships and relating lengths to the unit length to compute the needed values.
Other structures unsupported by JavaSketchpad are arcs, angle bisectors, dashed lines, points on polygonal interiors, to name a few. In addition, the Geometer's Sketchpad to HTML converter does not provide seamless conversion but attempts to convert the elements of a sketch that are permissible. Generally, the converter identifies sequences of geometric constructions that are not supported either because the construction utilizes an illegal object construction or a parameter not understood by the converter. This in turn required us to reconsider the underlying construction and develop it in a way to avoid the conflict.
Perhaps one of the most difficult limitations of JavaSketchpad is its inherent 2D nature. Although it would be beneficial to have students interact with the geometry of linear algebra concepts in higher dimensions, creating appropriate tools to aid those investigations using Geometer's Sketchpad is problematic. We have attempted to overcome these limitations, and this continues to be a work in progress.
To understand the visual limitation of rendering 3D on a 2D presentation device, we developed a Transformer3D tool to try to address some of the conclusions of Sierpinska et al. (1999) and Sierpinska (2000), who indicated that students who interact with linear algebra concepts from solely a two-dimensional perspective via Cabri geometry might misgeneralize concepts. Consequently, we thought appropriate and effective pedagogical activities are needed that integrate a variety of technological tools, such as web-based sketches with multiple dimensions, MATLAB activities, Maple or Mathematica investigations, and by-hand computations, thereby allowing students to investigate relationships in many dimensions and to develop their personal and collective understandings.
Next ![]() or
or ![]() or
or ![]() page: 14. Transformer3D Tool and Sample Activity
page: 14. Transformer3D Tool and Sample Activity
Tool Building: Web-based Linear Algebra Modules - Transformer3D Tool and Sample Activity
| |
| |
| |
Transformer3D was designed to complement Transformer2D by forcing students to grapple with transformations from R3 to R3, but doing so required us to adjust the way the student controls the development of the column vectors of the matrix of transformation. In order to overcome the 2D nature of Sketchpad and JavaSketchpad, we developed a means of representing 3D space on a 2D platform. Consequently, a vector's elements are controlled by moving sliders along the various axes. These sliders can in turn be used to further illustrate descriptions of vectors with respect to the natural basis.
Even though Transformer3D is not as polished as Transformer2D, it did provide opportunities for students to grapple with what it meant to construct transformations from R3 to R3. We designed Transformer3D to have a similar interface to that of Transformer2D. The controllers of the three column vectors of the matrix of transformation are maneuvered in the yellow box. The three vectors are controlled by sliders on the axes rather than by selecting the head of the vector and manipulating it in space. We implemented the sliders to allow for the three dimensions being rendered on a two-dimensional plane.
Below the yellow box is an area depicting the domain of the matrix transformation. For ease, the domain has been restricted to just the positive portion of the three axes. We provide an "animate points" button in this area, which randomly moves the vector x around in the restricted domain.
Two areas have been color coded to help students orient themselves. The larger area to the right contains a depiction of the range of the matrix transformation. The three vectors, a1, a2, and a3, are shown, along with the transformation of x with respect to the transformation T. In addition, students can choose to show or hide a wire frame, as well as observe the transformation of the two colored areas from the domain.
Open Transformer3D in new window
Note: The "?" at the bottom right-hand corner of the workspace is a link to Key Curriculum Press and its About JavaSketchpad web page.
Sample Exploratory activity:
Using Transformer3D, attempt to accomplish the following:
- Construct the matrix of transformation A =
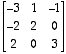 . Describe how this matrix transforms the unit cube. If you change one component of the matrix, for instance the -1 to a 2, how does that impact the image of the unit cube?
. Describe how this matrix transforms the unit cube. If you change one component of the matrix, for instance the -1 to a 2, how does that impact the image of the unit cube?
- Consider the matrix of transformation B =
 . Make a sketch of the image of the unit cube. Now, consider another matrix of transformation, C =
. Make a sketch of the image of the unit cube. Now, consider another matrix of transformation, C =  , and make a sketch of the image of the unit cube. What has changed between matrix B and matrix C? How did this change impact the shapes of the images of the unit cube? Try a couple other similar changes and see if you can you make any general conjectures.
, and make a sketch of the image of the unit cube. What has changed between matrix B and matrix C? How did this change impact the shapes of the images of the unit cube? Try a couple other similar changes and see if you can you make any general conjectures.
- Construct a matrix transformation that projects all points of the unit cube to a unit square. How many different ways can you accomplish this?
- Construct a matrix transformation, which is not the zero matrix, which has a degenerate image parallelepiped with zero volume.
- Construct a matrix A and then construct the matrix 2A. For each, observe what the image of the unit square looks like. Can you make any assertions concerning the change in volume of the images when you move from A to 2A?
Note: Transformer3D is quite sensitive, and it is difficult to obtain exact values and construct matrices containing coordinate values of 0 for multiple entries in the same column vector. This is one of the major flaws of attempting to render 3D pictures in a 2D environment.
Next ![]() page: 17. WebSVD Tool and Sample Activity
page: 17. WebSVD Tool and Sample Activity
Next ![]() or
or ![]() page: 15. Student Reactions
page: 15. Student Reactions
Tool Building: Web-based Linear Algebra Modules - Student Reactions
| |
| |
- "Moving individual pieces of a vector changes the position but not the shape of the transformed image".
- "The shape of the transformation of unit circle is dependent on the matrix A and not on x".
- "Although it's difficult to see what works with what, it was interesting to try to make the Transformation look like it was from R3 to R2. I really had to think about what I needed to change".
- "The 3D program helped me make sure my observations from the other one were right. I could test ideas and make sure they worked although sometimes it was hard to tell when things were moving".
Having students observe how different components of the matrix A impacted the nature of the transformation was the goal of constructing Transformer3D. In addition, having the students be able to make conjectures and then examine them in multiple settings has the potential to be valuable.
Next
Next ![]() page: 16. Discussion of Tools for Advanced Linear Algebra
page: 16. Discussion of Tools for Advanced Linear Algebra
Tool Building: Web-based Linear Algebra Modules - Discussion of Tools for Advanced Linear Algebra
|
|
One of the driving problems of advanced linear algebra, as encouraged by Strang (1988, p. 197), is the discussion of the singular value decomposition, for "the SVD has become fundamental in scientific computing." In particular, the SVD solves the problem of diagonalizing a matrix, which differs from an algebra-oriented course that might use the Jordan canonical form to answer that question.
By considering the question
What is the shape of the image of the unit circle under the transformation T(x) = Ax ?
we can nudge students toward thinking about the geometry associated with the transformation, rather than relying entirely on computations.
For instance, if we consider the matrix
we see this answer:

These pictures provoke two questions:
-
Is the image of the circle under the transformation T really an ellipse?
-
If it is an ellipse, what are the axes?
In the early years, Tom Hern and the late Cliff Long used hand-drawn pictures to motivate a discussion. Then, over time, technology allowed them to portray these pictures in a more professional manner -- but still static in nature. Finally, they used MATLAB to draw the unit circle, and, as the unit circle was traced out, the image curve would be traced. Now, with the advent of JavaSketchpad , the static pictures have become dynamic, web-based tools, namely WebSVD and Hern & Long SVD, allowing students to explore the singular value decomposition and explain the components of the SVD.
Next ![]() or
or ![]() or
or ![]() page: 17. WebSVD Tool and Sample Activity
page: 17. WebSVD Tool and Sample Activity
Tool Building: Web-based Linear Algebra Modules - The WebSVD Tool and Sample Activity
| |
| |
| |
The WebSVD tool, which is similar to those previously discussed, was originally written in MATLAB as part of the ATLAST project (Leon, Herman, & Faulkenberry, 1996), but the MATLAB platform has been frustrating from cross-platform and availability points of view. The web-based tool development presented here has breathed new life into that effort.
Specifically, WebSVD contains components similar to those of Transformer2D, but, given its purpose, it has different elements. The yellow box still controls the column vectors defining the matrix of transformation. In particular, the green vector is the first column, and the blue vector is the second column. By grabbing the ends of these two vectors, you can construct any 2x2 matrix. Below the yellow box is a box that controls the vector x, restricted to the unit circle. As you move x (the red vector) about the unit circle in the domain of the transformation, you can observe the image T(x) (the magenta vector) change in the large area depicting the codomain of the transformation. In addition, the vector x can be moved automatically about the unit circle. In order to further explore, a variety of buttons are provided in the codomain portion containing T(x). For instance, you can turn on or turn off a tracing feature that marks out the path of the transformed vector T(x) or show/hide the orbit of T(x). Also, you can superimpose x onto the codomain, as well as create a separate vector p in the domain and its transformation T(p). Each of these elements helps support exploration into the singular value decomposition of a matrix of transformation.
Open WebSVD in new window
Note: The "?" at the bottom right-hand corner of the workspace is a link to Key Curriculum Press and its About JavaSketchpad web page.
Sample Exploratory Activity:
Consider the transformation T(x) = Ax with matrix
Using WebSVD, grab the red vector x (hold down mouse button) in the yellow box and move it completely around the unit circle. What shape do you seem to be getting?
To get a better look, click the "Turn Trace ON" button at the bottom of the right box, and move the red arrow around the unit circle. What shape so you seem to be getting? If you want, you can click on one of the "Animate x" buttons to have the vector x move automatically. If you want the animation to stop, click the button again.
To clean things up a little, click on the "Turn Trace OFF" button, and click the red X in the lower right hand corner of the screen. You can still view the image shape by clicking on "Show Orbit of T(x)" at the top of the right box. You can keep one of the "Animate x" buttons on if you wish (but not both).
0. Experiment time
- With "Show Orbit of T(x)" selected, change the matrix of transformation and observe the image of the unit circle. Do we still get the same shape?
- Can you change the matrix to get a circle?
- Can you make the matrix symmetric? Orthogonal?
- Can you make the T(x) vector move in the opposite direction as x?
Play for a while.
1. What is it?
Experimentation should have led you to a feeling that the image of the unit circle appears elliptical. So, is it really an ellipse or not? If it is an ellipse, what are its axes?
A reasonable guess would be a set of eigenvectors from the matrix of transformation, A. Let's investigate that . . .
- Reload WebSVD to reset the matrix to the one we started with.
- Select the "Superimpose x" button at the top of the right-hand box, and select the "Show Orbit of T(x)" as well.
- Now, try to line up the x and T(x) vectors to find the eigenvectors.
Now consider the following questions:
- So, are these the axes?
- Do the axes of the supposed ellipse appear orthogonal?
- Do the eigenvectors appear orthogonal?
- Are the axes in the same directions as the eigenvectors?
Note: Since this is a triangular matrix, its eigenvalues are the diagonal elements: l1 = 1 and l2 = 1.5. Corresponding unit eigenvectors are x1 = (1,0) and x2 = 1/sqrt(10) (3,1) = (.9487, .3162). These are shown in the following figure with Ax1 = x1 and Ax2 = 1.5 x2 in the image.

2. Using the Geometry to find the SVD
We've eliminated eigenvectors as the axes of the ellipse, perhaps there is another way to find the axes.
Once again, consider the transformation T(x) = Ax with matrix
- Grab the red vector x (hold down mouse button) and move it around until the T(x) vector matches the major axis of the image ellipse. Record the vectors x and T(x), which are shown in the red bordered box. Also, record also the length of the vector T(x) -- it is at the bottom.
- Now select the "Show vectors p and T(p)" button. Move the x vector until the T(x) vector matches the minor axis. For comparison, move the vector p until T(p) matches the major axis of the ellipse. [We do this because the T(p) vector is not printed, only T(x).] You can use the angle measure that prints in the lower left corner to ensure that the axes are orthogonal. Record the same information about these vectors. Notice that the x and p vectors that correspond to the T(x) and T(p) vectors are also orthogonal.
- Use this information to write down the SVD of the matrix A.
If you need a hint, recall that x and p are eigenvectors of ATA, and T(x) and T(p) are the corresponding eigenvectors of AAT. The lengths of the vectors T(x) and T (p) are the square roots of the eigenvalues of ATA. Note: You can check your answer by asking Matlab: Enter A, then type "[Q1,Sigma,Q2]=svd(A)".
- Enter a new matrix that has rank one, and repeat Problem 1.
Next
Tool Building: Web-based Linear Algebra Modules - Hern & Long SVD Tool
|
|
|
|
|
|
Another means of examining singular value decompositions, described by Hern and Long (1991), is illustrated through the Hern & Long SVD tool, in which the decomposition is examined from the perspective of matrices of transformations that rotate, reflect, and stretch a unit circle to yield an ellipse. Rather than being an exploratory tool, this is an explanatory tool helpful for classroom discussions of the components of the SVD.
Consistent with the description of Hern and Long (1991), this tool contains a several regions that depict different aspects of the geometry associated with the singular value decomposition. As with most of our tools, the yellow box controls the column vectors defining the matrix of transformation. In particular, the green vector is the first column, and the blue vector is the second column. By grabbing the ends of these two vectors, you can construct any 2x2 matrix.
Next to the yellow box is the domain of the transformation that contains four vectors, x, p, v1, and v2. Vectors x and p are movable, with p restricted to the unit circle. Vectors v1 and v2 are restricted to the unit circle and dependent on the matrix of transformation. Specifically, v1 and v2 are the eigenvectors of the symmetric matrix ATA. The transformation defined by the matrix VT rotates the vectors v1 and v2 to the base vectors e1 and e2. Then, the matrix S stretches these base vectors by the factors  that are the lengths of the axes (and the positive square roots of the nonzero eigenvalues of AAT). Finally, the matrix U rotates these to Av1 and Av2. Consequently, the matrix A can be written as VTSU, where the entries si of S are called the singular values of A, and A = VTSU is called the singular value decomposition of A.
that are the lengths of the axes (and the positive square roots of the nonzero eigenvalues of AAT). Finally, the matrix U rotates these to Av1 and Av2. Consequently, the matrix A can be written as VTSU, where the entries si of S are called the singular values of A, and A = VTSU is called the singular value decomposition of A.
Open Hern & Long SVD in new window
Note: The "?" at the bottom right-hand corner of the workspace is a link to Key Curriculum Press and its About JavaSketchpad web page.
Next ![]() or
or ![]() or
or ![]() page: 19. Conclusion
page: 19. Conclusion
Tool Building: Web-based Linear Algebra Modules - Conclusion
| |
| |
| |
Our goal in this paper is to share the possible. Developing web-based linear algebra tools has been a long process and one fraught with its ups and downs. The expertise necessary to develop Java applets is enormous, and the learning curve is steep. This has left many educators with ideas but without the means to express them. When Key Curriculum Press introduced JavaSketchpad , they provided educators with a means of publishing Java applets that was less complicated although more restricted than programming completely in the Java language.
Our various implementations of Transformer, Grid-Master, Eigenizer, WebSVD, and Hern & Long SVD point to the potential efficacy of implementing web-based modules and correspondent cognitively-guided activities as part of linear algebra instruction. As a consequence, we have now reached a point where we have a truly viable way to construct and implement widely available interactive tools. The tools must of course be accompanied by well-designed activities that take advantage of both the power and limitations of the tools in order to help students learn mathematical content. Therefore, we see that the focus must now turn to the more difficult and lesser-studied topic: How to design materials and situations to take best advantage of such technology. Up until now this has been mostly anecdotal.
Next ![]() or
or ![]() or
or ![]() page: 20. References
page: 20. References
Tool Building: Web-based Linear Algebra Modules - References
Bevis, J. H. (2002). Multigrid Graph Paper. In D. Carlson, C.R. Johnson, D.C. Lay, & A.D. Porter (Eds.), Linear Algebra Gems: Assets for Undergraduate Mathematics (pp. 119-122). Washington, DC: Mathematical Association of America.
Carlson, D. (1993). Teaching linear algebra: Must the fog always roll in? The College Mathematics Journal, 24(1), 29-40.
Carlson, D., Johnson, C. R., Lay, D. C., Porter, A. D., Watkins, A. & Watkins, W. (Eds.). (1997). Resources for Teaching Linear Algebra. Washington, DC: Mathematical Association of America.
Carlson, D., Johnson, C. R., Lay, D. C., & Porter, A. D. (2002). Linear Algebra Gems: Assets for Undergraduate Mathematics. Washington, DC: Mathematical Association of America.
Dorier, J. L. (1991). Sur l'enseignement des concepts elementaire d'algebre lineaire a Ùniversite, Recherches en Didactique des Mathematiques, 11 , 325-364.
Dorier, J. L. (1995). Meta level in the teaching of unifying and generalizing concepts in mathematics. Educational Studies in Mathematics, 29(2), 175-197.
Dorier, J. L., Robert, A., Robinet, J. & Rogalski, M. (2000a). The obstacles of formalism in linear algebra. In J. L. Dorier (Ed.), On the Teaching of Linear Algebra (pp. 85-124). Dordrecht: Kluwer.
Dorier, J. L., Robert, A., Robinet, J. & Rogalski, M. (2000b). The Meta Lever. In J. L. Dorier (Ed.), On the Teaching of Linear Algebra (pp. 151--176). Dordrecht: Kluwer.
Hern, T. & Long, C. (1991). Viewing some concepts and applications in Linear Algebra. In W. Zimmermann & S. Cunningham (Eds.), Visualization in Teaching and Learning Mathematics (pp. 173-190). Washington, DC: Mathematical Association of America.
Hillel, J. (2000). Modes of description and the problem of representation in linear algebra. In J. Dorier (Ed.), On the Teaching of Linear Algebra (pp. 191-207). Dordrecht: Kluwer.
Jackiw, N. (1995). The Geometer's Sketchpad [Computer software]. Berkeley, CA: Key Curriculum Press.
Jackiw, N. (2001). The Geometer's Sketchpad 4.01 [Computer software]. Berkeley, CA: Key Curriculum Press.
Key Curriculum Press (2001). The Geometer's Sketchpad: Version 4 Reference Manual. Berkeley, CA: Key Curriculum Press.
Lay, D. C. (2003). Linear Algebra and its Applications (3rd ed.). Reading, MA: Addison-Wesley.
Leon, S., Herman, E. & Faulkenberry, R. (1996). ATLAST - Computer Exercises for Linear Algebra. Upper Saddle River, NJ: Prentice Hall.
MATLAB for the Macintosh [Computer software]. (1995). Natick, MA: The MathWorks, Inc.
Meel, D. E. (1999a). A linear algebra activity: From bases to matrices. MAA Online -- Innovative Teaching Exchange [On-line]. Available: /t_and_l/exchange/ite4/insearch.html (accessed 5/16/05)
Meel, D. E. (1999b). Learning logs: Enlivening elementary linear algebra. PRIMUS, 9(3), 205-225.
Sierpinska, A. (2000). On some aspects of students' thinking in linear algebra. In J. Dorier (Ed.), On the Teaching of Linear Algebra (pp. 209-246). Dordrecht: Kluwer.
Sierpinska, A., Dreyfus, T. & Hillel, J. (1999). Evaluation of a teaching design in linear algebra: The case of linear transformations. Recherches en Didactique des Mathematiques, 19(1), 7-41.
Strang, G. (1988). Linear Algebra and Its Applications, 3rd Ed. Harcourt Brace.
Watkins, A. & Watkins, B. (Eds.) (1993). Special issue on linear algebra [Special issue]. The College Mathematics Journal, 24(1).