Abstract

Elementary row operations, Gaussian elimination, and Gauss-Jordan reduction play key roles in an introductory linear algebra course. While some form of geometric visualization typically accompanies the introduction of these procedures, textbooks tend to focus nearly exclusively on their algebraic aspects. In this article, I propose a dynamic geometric illustration of elementary row operations, which can help students better understand Gaussian elimination and Gauss-Jordan reduction, from both mechanical and conceptual points of view.

Przemyslaw Bogacki is an Associate Professor of Mathematics at Old Dominion University .

In an introductory linear algebra course, elementary row operations are a recurring theme. They are typically introduced in the context of Gauss-Jordan reduction and/or Gaussian elimination and are repeatedly referred to when discussing a variety of topics, including matrix inverses, determinants, linear independence, coordinates, eigenvectors, and linear transformations (Carlson et al., 1993).

Almost all linear algebra textbooks incorporate at least some discussion of the geometry of vectors and lines in R², as well as vectors, lines, and planes in R³ . Specifically, there are renderings of planes in R³ corresponding to a system of equations in three unknowns (in various configurations: one solution, two parallel planes, etc.). See, e.g., Kolman and Hill (2001, p. 6) and Bretscher (2001, pp. 3-4). However, the mode in which elementary row operations are discussed in textbooks is almost exclusively algebraic.

Some authors have written modules, usually created on CAS platforms such as Maple or Mathematica, designed to overcome this limitation by illustrating the geometry of each iteration of Gaussian elimination (e.g., Symancyk, undated). I will take another step in this direction. Rather than presenting the iterations in a "discrete" manner, I will illustrate dynamically the transition corresponding to each row operation in a "continuous" fashion, using an animation-based approach. I believe this approach can help students better understand both the mechanics of how these operations are executed (e.g., "how we choose the pivot") and the motivation for the entire procedure of Gauss-Jordan reduction or Gaussian elimination (i.e., why we try to get these planes aligned with the coordinate axes).

To accomplish these goals, I have designed an activity called "HINGES" -- the acronym will be explained on page 3.

Published May, 2005

© 2005 by Przemyslaw Bogacki

I have recently class-tested this activity in a section of an Introductory Linear Algebra course with 35 students, most of whom were distance students at remote sites. (The Teletechnet system  operated by Old Dominion University allows for one-way video and two-way audio connection using a satellite broadcast. Additionally, some students participated in this class via video-streaming on their home computers.)

To proceed cautiously the first time around, I chose to make this a very low-stakes extra-credit activity. I promised up to two extra points on a class test for a successful completion of the activity, which was meant to be just a token of appreciation, as it amounted to less than 0.5% of the overall course grade.

I presented these modules after row operations were already covered -- mostly from the algebraic point of view -- so that students were already familiar with terms such as pivot, pivotal column, leading entry and reduced row echelon form . However, in the course of this activity, there was no mention of Gaussian elimination or elementary row operations. It was meant to challenge students to think about this model from a purely geometric point of view at first, subsequently to make the connection to the algebra of row operations.

The activity was deployed in three stages, spaced two days apart from each other, using our Blackboard system. This gave me the opportunity to track access to each of the stages by the individual students. My depiction of the activity on the following pages was modified to make it Web-based (rather than Blackboard-based).

The "Puzzle Leaflet"

In a rather tongue-in-cheek fashion, I posted the following document on the course Blackboard site:

"HINGES" - a virtual 3D puzzle An excerpt from a leaflet attached to a virtual puzzle called "HINGES" manufactured by DRB Enterprises. At the beginning of the game, you will see a cube containing three planes: red, green, and blue, as in the left picture below. 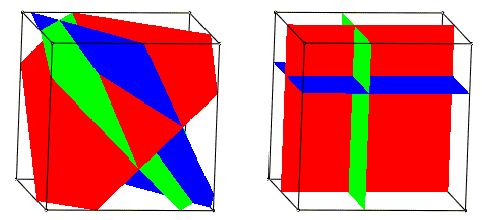(This cube is just a small portion of the R3 space, since the planes themselves are infinite). Your objective is to perform a sequence of legal moves to get each of the planes parallel to a different side of the cube, as in the picture on the right above. Each legal move is composed of these actions: Choose one of the three planes to be the door plane, another to be the wall plane - the remaining plane is the ghost plane. Using the hinge line (where the door plane intersects the wall plane), tilt the door plane to a new position (as far as you want), as if the ghost plane weren't there. Here are three possible initial choices for the ghost plane -- shown semitransparent -- and the corresponding hinge lines -- shown in black.

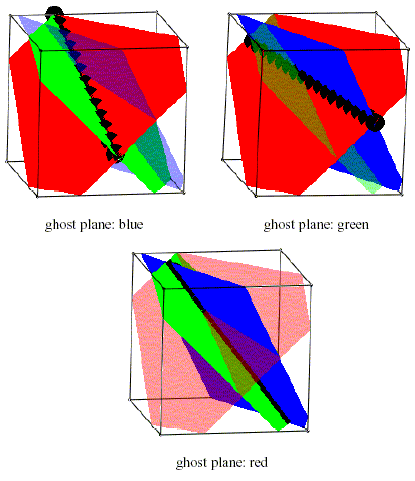I chose the name "HINGES" for this puzzle because selecting a hinge between two planes and rotating the "door" plane on the hinge are its key ingredients. Additionally, I wanted to avoid using any mathematical terminology in the name or in the leaflet that might suggest some ideas prematurely.

After reading the puzzle description, students were asked to try to think of a strategy to solve the puzzle in as few steps as possible.

I posed the following question, although I was not hoping for too many correct answers at this early stage:

Stop-and-go Animations

Two days later, I released the second stage module, which gave students the ability to perform a sequence of moves by watching frames of corresponding animations, and selecting the frames in which the proper alignment of the door plane is attained.

To keep things simple, each move in the animated sequence comes with a pre-selected choice of "door/wall/ghost" planes, as well as the cube edge (axis) with which the given door plane is to be aligned. In the original activity, this stage was implemented as a Blackboard Learning Unit, composed of a sequence of six assessments. In each assessment, the student was prompted to watch the animation corresponding to a move, then submit the answer (in "fill in the blank" format) containing the correct frame number, with a tolerance of either one or two frames in each direction.

Here is a "non-Blackboard" version  that emulates this functionality.

The Math Connection

The final stage of the activity is shown in the following handout:

I did not intend to offer any explanations just yet, but rather, to provide students some additional relevant information, as they should already be familiar with most of these ideas from their study of vectors, planes, lines, and cylinders in calculus.

This handout is meant to lead a student to

1. establish connections between the items used in the HINGES puzzle -- "hinge line", "door plane", "wall plane" -- and the intersection line and the planes discussed above, and
2. correctly identify the HINGES "moves" as elementary row operations on the augmented matrix of the system composed of the plane equations.

I designed the first stage to reveal initially relatively little information to get students to begin thinking about the problem. In subsequent stages I gradually provided additional clues -- both visual and analytic -- to help students succeed. I told the class that I would award full marks for the correct solution of the problem regardless of the stage during which the solution was submitted.

While the entire class of 35 students accessed the stage 1 "leaflet" document, they appeared to have difficulty solving the puzzle in the "virtual" mode. Only a handful of students submitted their solutions at that stage, and none of them were correct.

Sixteen students executed the sequence of moves in stage 2, almost all of them providing the correct frame number values, as expected. Three students submitted correct solutions, linking the puzzle to the Gauss-Jordan reduction and elementary row operations. Three additional students made the correct connection after studying the document in stage 3.

Having just six students out of 35 successfully complete this activity may not strike someone as a particularly impressive outcome. However, I viewed the experiment described here as a "proof of concept", and, in this sense, it has been successful. One can modify the activity described here to make its appeal broader, by providing additional information to students, increasing the credit value, etc.

At the conclusion of the activity, I posted the solution:

Every time we turn a door plane to make it parallel to one of the axes (x,y, or z), we end up removing the corresponding term from that equation (e.g., the plane 2y+3z=5 is parallel to the x axis). Therefore, each move corresponds to an elementary row operation, and the entire game corresponds to the Gauss-Jordan reduction leading to the reduced row echelon form.

I illustrated this by the animated sequence of correct HINGES moves along with the corresponding elementary row operations.

Here are a few additional points, which you may want to discuss with students after they participate in the HINGES activity:

• It can be shown that the combined equation (pa₁+qa₂)x + (pb₁+qb₂)y +  (pc₁+qc₂)z = pd₁+qd₂, resulting from taking a linear combination of the two non-parallel planes, generates all planes containing the line of intersection (the "hinge"). After students learn about subspaces of Rⁿ, this can be justified by considering the linearly independent normal vectors n₁ = < a₁, b₁, c₁ > and n₂ = < a₂, b₂, c₂ >, which span a two-dimensional subspace of R³ - the plane perpendicular to the line of intersection. Therefore, any plane containing the line of intersection has a normal vector that can be expressed as a linear combination pn₁ + qn₂ for some values p and q.
• In a row operation where k times the i-th row is added to the j-th row, the normal vector of the j-th plane is replaced with the linear combination of "old" normal vectors n_j + kn_i. The set of all such linear combinations does not form the entire 2-dimensional subspace mentioned above, as the vectors collinear with n_i are outside the set. Of course, this is the intended behavior of elementary row operations to prevent one of the equations from being overwritten with another.
• One aspect of elementary row operations that remains completely transparent under this illustration is the scaling of the matrix rows (and the corresponding normals). Such scaling is one of the outcomes of row operations of the type row_j + (k)row_i → row_j (in addition to the resulting rotation). Scaling can also be explicitly executed by performing an operation (k)row_i → row_i
• The third type of an elementary row operation, row_i ↔ row_j can, in the context of the HINGES puzzle, be viewed as resulting in altering the "door/wall/ghost plane" assignment sequence.

The HINGES activity could be used to compare geometrically the Gauss-Jordan reduction procedure (which transforms the augmented matrix to its reduced row echelon form) to Gaussian elimination (where row echelon form is used instead).

Also note that the rotation and scaling of a plane -- and of the corresponding normal vector -- can be discussed in a more concrete setting of linear transformations in R³ after this material has been reached -- see, e.g., (Anton, 2000, pp. 180-181).

I implemented the HINGES activity in a way that would make it compatible with a variety of systems and browsers. Teaching a class in a distance learning mode, no assumptions can usually be made about "standard" configurations, plug-ins, etc. The trade-off of this approach is that the interactivity available to a student is limited.

I am currently working on more interactive models, where a user can

• choose a different initial augmented matrix to work with,
• choose the sequence of "door/wall/ghost" plane selections -- for example, to try various pivoting strategies,
• rotate and zoom the 3D view (rather than dealing with the fixed view afforded by the pre-generated animations).

The following screen snapshot is taken from a Mathcad-based implementation of such an interactive model. The middle section of the document serves as a control panel: the radio buttons allow for altering the "door/wall/ghost plane" sequence, while the sliders control the rotation of the chosen door plane -- positioning the slider in the middle corresponds to no rotation.

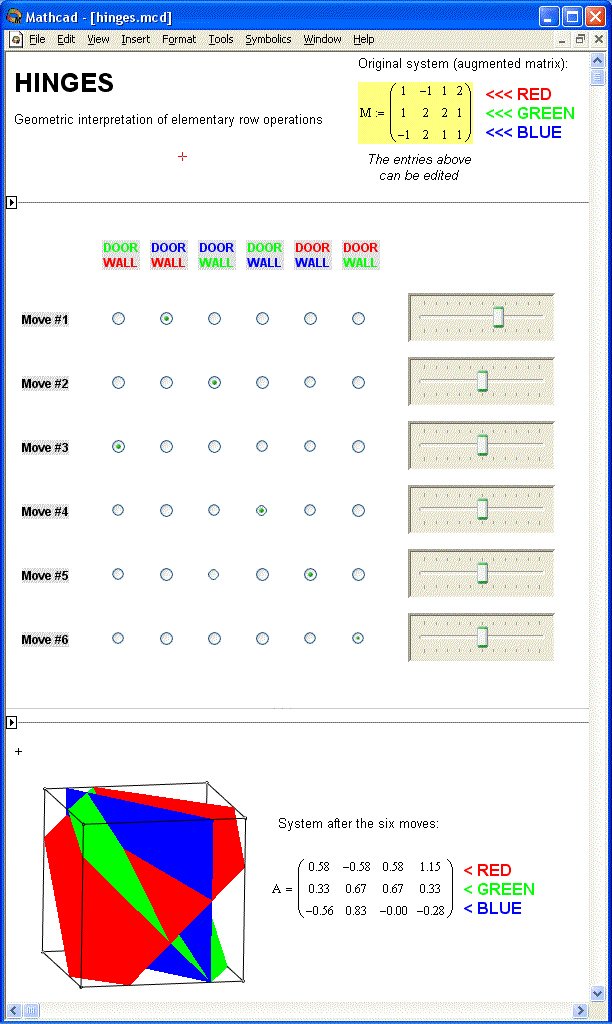
Among the future plans, I am considering creating a JAVA version of the HINGES activity that will provide at least the functionality of the Mathcad model.

I designed this activity for an introductory linear algebra class, without any emphasis on the numerical aspects. However, it may be very appealing to incorporate illustrations of this type when discussing Gaussian elimination pivoting strategies (Poole and Neal, 1991) in a numerical linear algebra course.

Anton, H. (2000). Elementary Linear Algebra, Eighth Edition, Wiley

Bretscher, O. (2001). Linear Algebra with Applications, Second Edition, Prentice Hall

Carlson, D., C. Johnson, D. Lay, & A. D. Porter (1993). "The Linear Algebra Curriculum Study Group Recommendations for the First Course in Linear Algebra", The College Mathematics Journal 24, 41-46

Kolman, B., and D. Hill (2001). Introductory Linear Algebra with Applications, Seventh Edition, Prentice Hall

Poole, P., and L. Neal (1991). "A geometric analysis of Gaussian elimination: Part I", Linear Algebra and its Applications 149, 249-272

Stewart, J. (1999). Calculus, Early Transcendentals, Fourth Edition, Brooks/Cole

Symancyk, D. F. (undated). Visualizing Gaussian Elimination, URL: http://ola4.aacc.edu/dfsymancyk/vgetalk/VGEtalkexpanded.html (accessed May 18, 2005)