A Framework for Technology-Rich Explorations - Introduction: Optimization Problems
Incorporating technology into the teaching and learning of mathematics has impacted various aspects of our instruction, from course content and teaching methodologies to classroom activities and assessment. The use of technology has encouraged us to re-examine our preconceived notions regarding the accessibility of various mathematical topics at various levels of instruction. As Quesada (2000) notes, ''the assumptions many of us made about mathematics curricula in a time prior to graphing calculators are, in many cases, no longer valid.''
Prior to the introduction of technology into mathematics classrooms, the types of problems that a typical student could solve depended largely upon his or her previous coursework. In such settings it was common for Instructors to identify an exercise as a ''precalculus'' problem or an ''advanced algebra'' problem based on the prerequisite mathematics skills required to generate a reasonable solution with pencil and paper.
Many calculus authors and instructors often treat optimization ("max/min") as their own domain, as if it had never been seen anyplace else, and in traditional curricula, such problems were often deferred to calculus. Historically, activities involving optimization, such as the "Two Towers Problem" (TTP) in Figure 1, were considered calculus problems. Because traditional solutions to activities such as the TTP often prompted the use of trigonometry and differential calculus, such problems were considered inaccessible to first-year algebra students using pencil-and-paper techniques.
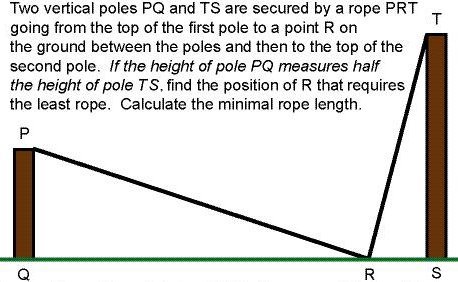
Figure 1. The Two Towers Problem (Source: Adapted from Stewart, 2001 )
As we've introduced technology-based problem-solving tools in our classrooms, the distinctions among activities appropriate for students at various instructional levels have become less clear to us. For instance, students in our developmental courses typically possess little or no knowledge of trigonometry or calculus. Nonetheless, they successfully build models and solve the TTP using dynamic geometry tools (such as Geometer's Sketchpad or Cabri Geometry II). In fact a whole host of optimization problems, traditionally not introduced to students in courses prior to calculus, may now be modeled in this fashion.
Some examples of other easily accessible optimization problems
Clicking and dragging points within their models, our students generate and test conjectures regarding relationships among different variables in their sketches. In the TTP, students look for relationships among lengths (e.g. QR), angle measures (e.g. angles PRQ and TRS), and minimal rope length. As they study algebraic concepts, our students investigate the TTP as a technology-based data analysis activity. After collecting data from physical models, they use calculator-based regression tools to compute ''fit'' equations that describe the relationship of QR to total rope length. In short, students at various levels may use technology meaningfully to explore problems previously constructed for the most advanced mathematics students.
On the next page we describe a framework that may be useful for both instructors and students as they explore mathematics in technology-rich settings. This framework has proved useful for us as we've constructed problems for our students to explore with technology from a variety of perspectives.
Our students have also used the framework to compare the relative advantages and disadvantages of various technology-oriented problem-solving approaches. When our students possess multiple solution strategies for a given problem, the likelihood of their generating mathematically correct solutions is enhanced significantly. In addition, exploring problems from several vantage points encourages our students to build connections among various areas of mathematical study.
Classroom instruction that explicitly explores and compares various solution strategies enhances our students' problem-solving power. Considering that more than half of college math enrollments are at the high school or developmental level, we feel that such explorations are quite relevant for all these students and equally important for pre-service teachers. Although our students use a variety of different tools to solve problems such as the TTP (e.g. Excel, Derive, Mathematica, Maple), in this article we pay particular attention to solutions that use graphing calculators, since their cost and portability make them a popular choice among many high school and college students.