Using computers to allow students to “do mathematics” is not a new idea. Fisher and Jones (1987) used Logo in a course for upper division mathematics majors and high school mathematics teachers to allow the participants to investigate, conjecture, prove, and systematize. Providing such an opportunity takes on added significance in the face of the recent focus on the need to infuse mathematical thinking in the classroom (National Council of Teachers of Mathematics, 2000; National Commission on Mathematics and Science Teaching, 2000; Mid-Atlantic Eisenhower Consortium for Mathematics and Science Education, 1998), the apparent perceptions that junior high and high school teachers have of the role of proof in mathematics in the classroom (Knuth, 2002), and questions about undergraduates’ understanding of the role of proof in mathematics (Moore, 1994). More recently, Martinez-Cruz et al.  (2004) has used Geometer’s Sketchpad (GSP) in a course for upper division mathematics majors and high school mathematics teachers for the purpose of having the students discover “new” mathematics.

Jorgen Berglund is an Assistant Professor of Mathematics at California State Univeristy, Chico.

This article recounts a full mathematical experience I was able to create for in-service teachers in a Dynamic Geometry course taught in the summer of 2002. GSP played a central role in this experience. While the topic of the course was Euclidean geometry and the audience working teachers, the implications of the article are important for anyone interested in the potential of integrating technology in mathematics classes and in the pedagogical implications of creating a full mathematical experience for students. The software itself is versatile, as seen in its use in Tool Building: Web-based Linear Algebra Modules, (Meel and Hern, 2005).

My course was the fourth in a series of eight new courses being designed for in-service mathematics teachers as part of a proposed Master’s program. The three previous courses had been offered during the school year, one each quarter. The students were diverse: junior high school and high school teachers, some with a mathematics degree and some who had had little more than a calculus course; some with years of experience teaching and some who hoped to become teachers; some who had taken the previous courses in the series and some for whom this was the first. While I wanted the students to become familiar with GSP, the focus of the course was to be mathematics, with GSP only a tool used in the study of the mathematics.

Seeking to take advantage of the power of this tool, and looking for a way of engaging this diverse class, I assigned the following class project: Everyone was responsible for contributing something new to the mathematical knowledge of the class. This contribution could come in the form of an interesting question, investigation, conjecture, proof, or systematization of the new conjectures and theorems. I would pose some initial questions and collect and report on the ongoing work. I required that the contributions extend what we had been studying or blaze new ground in some way. While “new to the class” allowed for “discovery” of already known mathematical relationships, I hoped that truly new mathematics might arise from the work. I encouraged students to ask their own questions and start their own investigations.

Published September, 2005

© 2005 by Jorgen Berglund

 

The first open question came as an extension of our first investigation from Rethinking Proof (de Villiers, 1999). In the dynamic environment provided by GSP, the students summed the measures of the distances to the sides from a point on the interior of an equilateral triangle. By moving the point inside the triangle, students observed that the sum remains constant. The conjecture can be proven, as indicated in the text, by decomposing the equilateral triangle into three triangles, each of which has one of the distances as the length of its altitude (Figure 1).

Figure 1: Distances to the Sides of an Equilateral Triangle

The title of Figure 1, like others to follow, links to a JavaSketchpad file that allows you to explore the sketch interactively. While these files don’t have the robustness of a full Sketchpad file, they do allow you to get a feel for the investigations. 

Note: If you encounter any difficulty with the JavaSketchpad file, see Mays (2003) for explicit instructions.

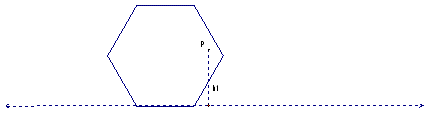
A follow-up question in Rethinking Proof (de Villiers, 1999) asks students to extend the triangle result to polygons with "a similar property." Since the proof of the initial theorem depends on the congruency of the sides of the triangle, the students tended to extend the results directly to equilateral polygons. However, the result does not generalize in this way, since there are points on the interior of most equilateral polygons for which the perpendicular from the point does not intersect the side, but rather extends outside the polygon, as in Figure 2.

Figure 2: Distance to the Side of a Hexagon

To set the stage for the first open question, I pointed out that the conjecture could be modified to read "the sum of the distances from a point on the interior of an equilateral polygon to the lines containing the sides is constant." This then could be proven in the same manner as the original case. However, the following question remained:

For a given equilateral polygon, what is the region for which the sum of the distances to the sides of the polygon from a point on the interior is constant?

One of the results of posing the question was the apparent awkwardness of referring to "the sum of the distances to the sides of the polygon from a point on the interior is constant" each time we wanted to discuss the question. As a result, the class came up with the following definitions.

Definition: The constant sum region (CSR) of a polygon is the region interior to the polygon for which the sum of the distances to the sides is constant.

Definition: The distance sum of a point is the sum of the distances from the point to the sides of a given polygon.

The distance sum of a point was defined after the class discussion on the CSR, and thus was not incorporated into its definition. The role definition plays in mathematics was not well understood by most students in the class. This was illustrated by earlier conversations in which Euclid's definition of a parallelogram was characterized as "wrong" since it was not the same as the one the teachers were familiar with. Having the participants in the class experience first-hand the creation of definitions out of need appeared to be a valuable lesson.

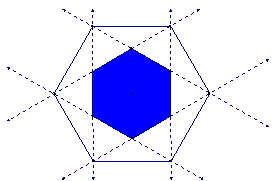
The first conjecture was quick in coming. Before the end of the class in which the question was posed, one student had constructed the constant sum region for a regular hexagon and made a conjecture. It is interesting to note that this student was one who had a minimal mathematics background. Following some suggestions I gave, the student made this conjecture.

Conjecture: The CSR for a regular hexagon is a smaller regular hexagon that has been rotated 30 degrees with respect to the original hexagon. The area of the CSR is one third of the area of the original hexagon, and the length of a side is approximately .577 the length of the side of the original. (L. Miller)

Figure 3: The CSR for a Regular Hexagon

The ease with which the conjecture was made is due in large part to the construction and measurement tools available in GSP. The fact that the conjecture contains an approximation is to be expected, as the conjecture was based on GSP measurements. In proving this conjecture, the students discovered that 0.577 is an approximation for.

Note: The students whose work is cited in this article have all given permission for their names to be used.

At this point some students decided to investigate other regular polygons. In addition, proofs of parts of this conjecture were made by several different students using a variety of arguments. They all assumed the CSR of a regular polygon is a hexagon, a point that was only informally argued. Given the time limits of the class, it seemed reasonable to assume this result. The results at this point in the project are summarized in the following conjectures and theorems. In proving parts of his original conjecture, L. Miller's understanding of the relationships deepened, as exemplified by his recognition of the actual ratio of the side of a regular hexagon to the side of its CSR.

Theorem: Assuming the CSR region for a regular polygon is a hexagon, it is an equiangular hexagon. (F. Rocha)

Theorem: The ratio of the area of a regular hexagon and its CSR is 3:1 and the ratio of the side of the regular hexagon to the side of the CSR is . (L. Miller, L. Cooke, R. Rocha)

Conjecture: The CSR for a regular 2n-gon is a regular 2n-gon, while the CSR for a regular (2n  + 1)-gon is a regular (4n  + 2)-gon. (M. Castro, L. Cooke)

In the course of the next few weeks, several students actively worked on the question of the CSR for equilateral polygons. F. Rocha proved that the CSR for a regular hexagon is not only equiangular, but is in fact regular. L. Cooke extended his analysis to regular 2n-gons and (2n  + 1)-gons. This work can be summarized by the following conjectures. L. Cooke proved the last three conjectures only for a number of specific values of n , but his methods would lend themselves to a proof of the general case stated in each conjecture.

Conjecture: The sides of the CSR for a 4n-gon are parallel to the sides of the 4n -gon.

Conjecture: Let  be the central angle (the angle formed by joining two adjacent vertices to the center of the regular n-gon) of a regular 2n-gon, n  > 2. Then the ratio of the length of the sides of the 2n -gon to its CSR is . The ratio of the areas is .

Conjecture: The length of the apothem (the segment measuring the distance from the center to a side) of the CSR for any regular n-gon is half the length of the side of the n -gon.

Conjecture: For any (2n+1)-gon, n  > 1, and its CSR, the ratio of the lengths of the sides is and the ratio of the areas is .

Shortly after the question of the CSR was posed, I posed a second open question to the students. I first saw this question on the CSU, Chico Department of Mathematics Web page, posted as a challenge question for high school geometry students. According to Jim Jones, Professor of Mathematics at CSU, Chico, no responses were ever received. It has since been replaced by other challenge problems.

I had used the question on several different occasions to illustrate the potential of GSP. The Dynamic Geometry students, save one, first saw the question on their take-home midterm. Each student was instructed to work independently on the question. The student who had seen the problem before was able to draw from that experience, but this did not adversely affect her or the class’s experience.

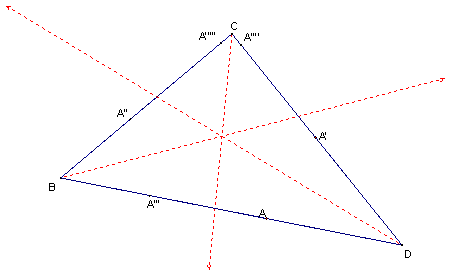
Construct a triangle and an arbitrary point on one side. Moving in a counterclockwise direction, reflect the point across the angle bisector of the adjacent angle. Continuing to move in a counterclockwise direction around the triangle, reflect the new point across the next angle bisector. Continue this process. Make and prove conjectures on whether this process will eventually lead back to the original point. Looking at specific types of triangles may lead to partial or additional results.

Figure 4: Reflection over Angle Bisectors

Click on the title for the JavaSketchpad version. If you have Geometer's Sketchpad, you can download and run the GSP file.

My class of 19 students generated a substantial list of conjectures from this one question. In my role of coordinator, I modified the language but not the main thrust of the various conjectures, and I supplied the following list and instructions to the class. For instance, I introduced the term “return time” to replace the various ways the students described the number of reflections until the point was reflected back to its original position.

A great deal of work has been done on the third problem on the take-home portion of the midterm. In this problem, a point on the side of a triangle is successively reflected across the angle bisectors. This problem is being moved over to the domain of the class project since there seems to be substantive work left. Here I will attempt to list the results so far. This list was quickly compiled, so the person cited was the person on whose paper I first saw the conjecture. My apologies to those who independently made the same or similar conjectures. I will attempt to rectify this in future updates. Since these results were obtained from the take-home exam, they do not count for credit towards the individual’s project grade; however, continued work will. I did not have time to determine which of these conjectures were proven.

Conjectures

1. All points on all triangles have a return time of at most six (C. Rojas, et al).
2. The mid-point of a side of an equilateral triangle has a return time of three (D. Taylor).
3. The mid-point of the base of an isosceles triangle has a return time of three (B. Campoy).
4. Every side of a triangle has a point whose return time is three (C. Rojas).
5. In a triangle, the three points whose return time is three are the three points of tangency of the inscribed circle (L. Cooke).
6. The points formed by the successive reflections of a point are co-circular (C. Finzell)
7. Reflecting points across the angle bisectors is equivalent to rotating these points around a point centered at the incenter of the triangle (F. Rocha).
8. A point, its reflection across an angle bisector, and the vertex of the angle form an isosceles triangle (C. Tedder).
9. The reflection of a point on the side of an angle across the angle bisector will lie on the line containing the other side of the triangle (D. Taylor).
10. The vertex of an equilateral triangle will have a return time of five (D. Taylor).
11. The point on the side of an isosceles triangle whose distance from the vertex is equal to the distance of the point on the second side formed by the intersection of the angle bisector has a return time of three (B. Campoy).
12. The vertex of an equilateral triangle has a return time of four (B. Campoy).
13. Given triangle ABC and point X on segment AB, the distance of X to B must be less than the length of BC for the point’s reflection across the angle bisector of B to lie on segment BC (B. Campoy).

There were indeed proofs and partial proofs contained in students’ work. The following suggested proof was supplied by C. Rojas, who was the one student who had seen this problem when I used it in a previous course. In later communication with me, she indicated that her previous exposure to the problem and the proof then outlined guided her in her work.

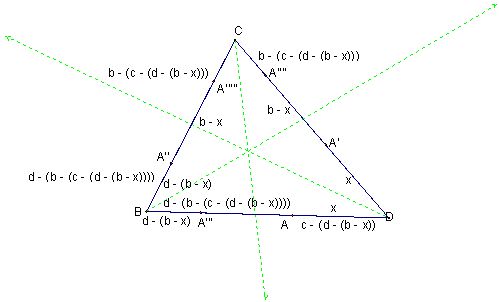
Consider with sides of lengths , respectively. (See Figure 5.) Select point on side and label the distance from to vertex as . The image of under a reflection across the angle bisector of , , is also a distance from , and therefore a distance from vertex .

As a consequence, , the image of  under a reflection across the angle bisector of angle , is a distance from vertex , and a distance from vertex .

The next reflection across the angle bisector of , results in a point, , whose distance from is .

This is followed by a second reflection across the angle bisector of , resulting in a point whose distance from is .

The next reflection is across the angle bisector of angle , and the image, , is a distance .

The sixth and final reflection, across the angle bisector of angle , results in a point whose distance from is , therefore returning to the position occupied by the original point .

Figure 5: Return Time of 6 in a General Triangle

The class was generally impressed by this argument and considered it a valid proof. This provided an opportunity to examine the assumptions underlying the argument.

For instance, the argument assumes that the images of the points under reflection will lie on the line containing the side of the triangle. Since this can be proven -- in fact was proven by several students -- it provided an example of the role of lemmas in mathematical proofs as well as an understanding of the importance of dialog between mathematicians.

A second issue, one that was not raised in class, is the assumption that all points lie on the sides of the triangle as opposed to the lines containing the sides. In other words, there is an assumption that each subtraction results in a positive value. Since a simple adjustment can be made in Rojas’ argument to address this issue, her argument is substantially correct.

Another student, D. Taylor, approached the problem from a different perspective. He first proved the following lemmas.

Lemma: The reflection of a point on the side of an angle across the angle bisector will lie on the line containing the other side of the angle.

Lemma: A point and its reflections are all equidistant from the incenter of the triangle.

Lemma: The composition of the reflections across two concurrent lines is equivalent to a rotation about the point of intersection.

These lemmas led to a proof of the theorem, and in subsequent class discussions the class consensus was that this proof was superior to the first. It not only led to a generalization of the results to n-gons with concurrent angle bisectors, but it suggested a fundamental switch in perspective. The issue was not one about points on the side of a triangle being reflected across angle bisectors, but about arbitrary points being reflected across concurrent lines. The fact that the concurrent lines happened to be angle bisectors of a triangle whose side contained the initial point was seen as incidental.

A number of students had already investigated related questions. C. Lambie had conjectured that a general point taken on the interior or exterior of the triangle had a return time of 6. C. Finzel, M. Elliot, and B. Salam had made the same conjecture about reflections across perpendicular bisectors, altitudes, and medians of a triangle. The class noted with appreciation that all of these conjectures were special cases of a more general theorem that reflections about concurrent lines will have a return time related to the number of lines.

Others, such as L. Miller, had found experimentally that for most (non-regular) quadrilaterals, the reflection points did not return, and that the cases in which they did return were precisely the cases were the angle bisectors were concurrent. We felt as though we had come closer to the deeper, more essential, relationship.

We briefly discussed the question of return times less than 6. It was not clear if D. Taylor’s proof would account for these, but apparently C. Rojas’ proof could. D. Garber then analyzed D. Taylor’s proof and claimed to have shown how return times of 5 and 3 could be accounted for, at least in certain cases. There were others who investigated those points that had a return time of less than 6, finding that there exist points with a return time of 5 (M. Hellman, M. Elliot, C. Tedder).

One last area of contribution was an attempt to systematize the results of the point-reflection investigations. This proved to be very challenging and led to a class activity in which various groups presented suggested systems. These were of various degrees of sophistication but led to a general realization that, in order to systematize the results, one needs to know a proof of each of the results. The discussion ended with a recognition of the role proof plays in systematization of mathematical theorems (de Villiers, 1999).

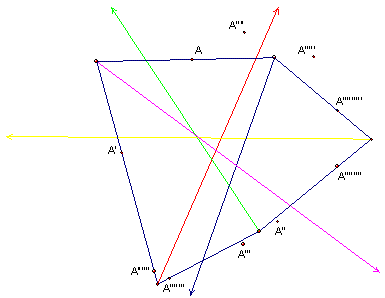
With most of the class satisfied that we now understood the underlying reasons that the reflected points returned, the last day of class provided a dramatic lesson in the complexity of mathematical relationships. P. Henson came in with a result that a general point on the side of an arbitrary pentagon has a return time of 10. The proof followed the method of C. Rojas. What was so shocking about this result is that the angle bisectors are distinctly not concurrent, and the reflections are not co-circular. (See Figure 6.)

The class ended with a sense that we had uncovered more questions than we answered. This was a fitting ending to the class project, as this final realization is a common feature of mathematics research.

Figure 6: Reflection over Angle Bisectors in an Irregular Pentagon  

Click on the title for the JavaSketchpad version. If you have Geometer's Sketchpad, you can download and run the GSP file.

A majority of the class contributed to and were engaged in the class project. The issues that came up individually and as a class were mathematically rich and led to numerous realizations for the class about the nature of mathematics. Students experienced mathematics as a process of discovery and analysis.

The role of proof in this process was varied. It was a tool for understanding, discovering, verifying, systematizing, and communicating.

Definitions were experienced not as static, but as evolving tools in mathematical thinking and communication.

The versatility and power of dynamic geometry software made this situation possible. It allowed students to explore relationships, follow up on ideas, and test hypotheses. Students became participants in a mathematical experience in a way that would have been difficult, if not impossible, to create without such a program.

de Villiers, M. (1999). Rethinking Proof with Geometer’s Sketchpad, Key Curriculum Press

Fisher, W., and J. Jones (1987). “Doing Mathematics in a LOGO Environment”, Academic Computing, 2, no. 4

Knuth, E. (2002). “Secondary Teachers’ Conceptions of Proof”, Journal for Research in Mathematics Education, 33, no. 5, 379-405

Martinez-Cruz, A., R. McAlister, and G. Gannon (2004). “Ron's Theorem and Beyond: A True Mathematician and GSP in Action”, Mathematics Teacher 97, no. 2, 148-151

Mays, M. (2003). “Quick Interactive Web Pages with Java Sketchpad”, Journal of Online Mathematics and its Applications, retrieved September 1, 2005 from http://www.mathdl.org/mathDL/4/?pa=content&sa=viewDocument&nodeId=508

Meel, D., and T. Hern (2005). “Tool Building: Web-based Linear Algebra Modules”, Journal of Online Mathematics and its Applications, retrieved September 1, 2005 from http://www.joma.org/mathDL/4/?pa=content&sa=viewDocument&nodeId=560

Mid-Atlantic Eisenhower Consortium for Mathematics and Science Education (1998). TIMSS, A Source Book for 12^th-Grade Findings, Research for Better Schools.

Moore, R. (1994). “Making the Transition to Formal Proof”, Educational Studies in Mathematics, 27, no. 3, 249-266

National Commission on Mathematics and Science Teaching for the 21st Century (2000). Before It’s Too Late, a Report to the Nation, U.S. Department of Education,

National Council of Teachers of Mathematics (2000) NCTM Principles and Standards for School Mathematics, NCTM