Can You Really Derive Conic Formulae from a Cone?
In this article we will see how ancient Greek geometers discovered and constructed conic sections. The modern equations of the conic sections are derived from Greek sources using only high school mathematics, mostly the theory of similar triangles. We also make use of GeoGebra to better illustrate the relationships involved in the derivations.
Editor's Note: This article was originally published in the inaugural edition of Convergence in April of 2004. We are pleased to "reprint" it in June of 2015 with 17 interactive GeoGebra applets that take advantage of GeoGebra's new 3D capability, hosted by GeoGebraTube.
Can You Really Derive Conic Formulae from a Cone? - Introduction
As is the case with a great deal of interesting mathematics, the conic sections are believed to have been discovered in an attempt to solve a problem, a problem which on the surface seems to have nothing to do with conic sections. The problem is the problem of doubling the cube, one of the three famous problems of antiquity. While we are not certain as to the exact moment of discovery, most authors attribute it to Menaechmus (4th century B.C.) [8, pp. 251-253]. The evidence for this is based on a work of Eutocius (6th century A.D.), Commentary on Archimedes’ Sphere and Cylinder. In this work Eutocius describes solutions to the problem of doubling the cube, that is, constructing a cube with twice the volume of a given cube.
As we shall now see, this problem is reduced to the problem of finding two mean proportionals between two given lengths. To see this, consider a cube of side a. We wish to construct the lengths x and y (the two mean proportionals) such that
a : x = x : y = y : 2a.
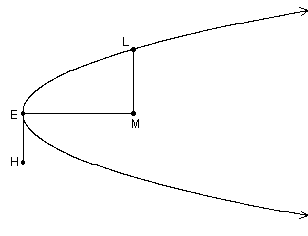
Before we see how Menaechmus constructed these mean proportionals, we must review the meaning of the "latus rectum" of a conic. The latus rectum of a conic is the chord through the focus parallel to the directrix. (The focus and the directrix can serve to define a conic section.) In the diagram below, you can see how the latus rectum controls the "opening" of a parabola.
What follows is Menaechmus' construction, according to Eutocius, of the two mean proportionals between two given lengths. (Note that Menaechmus did not use the terms "parabola" and "hyperbola." They were coined later by Apollonius.)
Can You Really Derive Conic Formulae from a Cone? - Menaechmus' Constructions
Let us consider how Menaechmus constructed the two mean proportionals. [14, pp. 278-283]. Let the given lengths be a and b. Let a straight line be given to serve as the axis, with a point D on the line to serve as the origin. Construct a parabola with the given axis, with vertex at D, and latus rectum a. This is equivalent to constructing a square on ordinate y equal to the rectangle on the latus rectum with side x. Note that this makes y the geometric mean of the latus rectum and the side x. Consider the diagram below to see why.
The height of the rectangle is x, the abscissa.
You can change the latus rectum a. Click “Trace” and then “Animate” to construct the parabola.
From the above sketch you can convince yourself that this does indeed generate a parabola.
Next, using the same axis and origin as above, construct a hyperbola such that the rectangle contained by the abscissa x and the ordinate y makes an area equal to the area of the rectangle contained by the lengths a and b.
The base of the rectangle at lower left is a; the height is b.
You can change the constants a and b. Click “Trace” and then “Animate” to construct the hyperbola.
From the above sketch you can convince yourself that this does indeed generate a hyperbola.
Now, what about the mean proportionals of a and b? The abscissa x and ordinate y of the point of intersection of the hyperbola and parabola so generated give the mean proportionals of a and b .
You can change the constants a and b.
Click “Trace” and then “Animate” to construct the parabola and hyperbola and then make note of the point of intersection.
In this manner, Menaechmus constructed the mean proportionals to a and b. If we let b = 2a, we have found the side x of a cube with double the volume of a cube with side a. It is important to point out here that this does not solve the problem of doubling the cube as the Greek geometers intended. This solution cannot be completed with ruler and compass only, and hence is not a solution.
Can You Really Derive Conic Formulae from a Cone? - Why Do Menaechmus' Constructions Work?
Reconsider the mean proportionals x and y of a and 2a: a:x = x:y = y:2a. With the help of modern analytic geometry, we see that this is equivalent to solving simultaneously two of x2 = ay, y2 = 2ax, and xy = 2a2. You should notice immediately that x2 = ay and y2 = 2ax are equations of parabolae, and xy = 2a2 is the equation of a hyperbola. Solving these equations simultaneously is equivalent to intersecting these conics.
Taking the second and third equations and solving them simultaneously gives x3 = 2a3, so a cube of side x has double the volume of a cube of side a.
Was Menaechmus the first to use conic sections? In the same work by Eutocius we have a description of Eratosthenes' (3rd century B.C.) solution to the problem of finding two mean proportionals. In regards to the merits of his own solutions, Eratosthenes is quoted as saying "Do not seek to do the difficult business of the cylinders of Archytas [another method of solution], or to cut the cone in the triads of Menaechmus, or to produce any such curved form in lines as is described by the divine Eudoxus." [14, p. 297]. Based on this quote, it would seem that the "triads of Menaechmus" refers to the three conic sections (we have not yet discussed the ellipse at this point). Because of this Menaechmus is given credit for discovering all three conic sections.
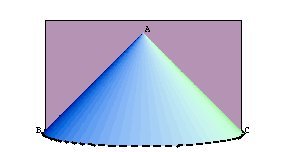
Did Menaechmus actually take sections of a cone? We do not know. The parabola and hyperbola can be constructed pointwise using the geometry of Menaechmus' time. The pointwise generation of the parabola looks something like the graph below.
It is not too hard to imagine the circles in the picture above as horizontal slices of a slanted cone, as shown in the picture [11, p. 117] and GeoGebra animation below.

In the window below, right click and drag to change the viewing angle of the slanted cone and its level curves.
Scholars have taken up this idea and have given probable constructions of conic sections based on sections of a right angled cone [5, pp. 1-4] [9, pp. 111-116]. We take up this discussion in the next sections.
Can You Really Derive Conic Formulae from a Cone? - Conics as Orthogonal Sections of Cones - Introduction
According to Pappus in his Collection from the fourth century, "Apollonius, who completed the four books of Euclid's Conics and added another four, gave us eight books of Conics. Aristaeus, who wrote the still extant five books of Solid Loci supplementary to the Conics, called the three conics [the] sections of an acute-angled, right-angled and obtuse-angled cone respectively." Pappus goes on to say that "Euclid regarded Aristaeus as deserving credit for his contributions to conics, and did not try to anticipate him or to overthrow his system .... Accordingly he wrote so much about the locus as was possible by means of the Conics of Aristaeus, but did not claim finality for his proofs." [14, p. 487]
Unfortunately, we know little about Aristaeus, and while his Solid Loci was extant in Pappus' time, it is lost now. Euclid's Conics is lost as well, but from Pappus' description the work was likely a book containing the "state of the art" of conics at the time, much like Euclid's Elements represented the culmination of the basics of geometry at the time. Aristaeus' time is placed in the late fourth century B. C., after Menaechmus, and before Euclid (ca. 300 B.C.). Fortunately, Archimedes (287 - 212 B.C.) writes a great deal about properties of conic sections, and he refers in his works to "the elements of conics," which we may infer as the works of either Aristaeus or Euclid, or both. In this way Archimedes provides some evidence as to what was in these works.
Recall that on Pappus' evidence we know that Aristaeus and Euclid considered sections of acute-angled, right-angled and obtuse-angled cones. We do in fact have Euclid's definition of a cone, in Elements Book XI, Definitions 18-20:
Def. 18. When a right triangle with one side of those about the right angle remains fixed is carried round and restored again to the same position from which it began to be moved, the figure so comprehended is a cone. And, if the straight line which remains fixed equals the remaining side about the right angle which is carried round, the cone will be right-angled; if less, obtuse-angled; and if greater, acute-angled.
Def. 19. The axis of the cone is the straight line which remains fixed and about which the triangle is turned.
Def. 20. And the base is the circle described by the straight line which is carried round [10].
At this time conics were intersections of a plane at right angles to the side that when rotated generates the cone. Let's see how this generates the three conic sections:
Above: The section of a right-angled cone (also known as an orthotome, now known as a parabola)
Right click and drag to change the viewing angle.
Above: The section of an acute-angled cone (also known as an oxytome, now known as an ellipse)
Right click and drag to change the viewing angle.
Above: The section of an obtuse-angled cone (also known as an amblytome, now known as an hyperbola)
Right click and drag to change the viewing angle.
While we know how the conics were generated, what we do not have is evidence of how the symptom of the conic is derived. The symptom is the relationship between the abscissa and ordinate of a point on a conic that determines which type of conic is present. (Today we would express this as something like y = x2). Using the geometry of the day, however, we can see how the symptom of a conic might have been derived. We will consider the section of a right-angled cone later, so first consider the oxytome, the section of an acute-angled cone.
Can You Really Derive Conic Formulae from a Cone? - Deriving the Symptom of the Acute-angled Cone
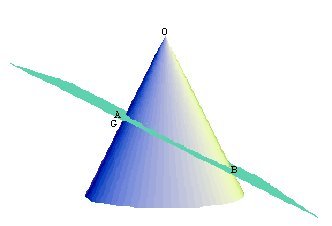 Consider the acute-angled cone with vertex O and a plane intersecting a generating line OG at a right angle at point A. The plane intersects the cone in the oxytome with diameter AB.
Consider the acute-angled cone with vertex O and a plane intersecting a generating line OG at a right angle at point A. The plane intersects the cone in the oxytome with diameter AB.
A dynamic view of this construction will be helpful in what follows.
[In order to open the dynamic view in a new window to allow you to show the text and the derivation side-by-side, right click or Ctrl-click on the link.]
 |
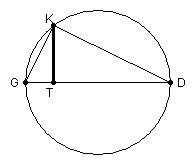 |
Consider an arbitrary ordinate (i.e. y value) TK constructed on the axis at T. We wish to determine the relationship between TK and AT, that is, the symptom of the conic. The ordinate TK is located in a horizontal plane that cuts the cone in the circle with diameter DG. In this horizontal plane construct the segments GK and DK, which results in a right triangle inscribed in a semicircle. (The triangle is right by Elements, Book III, Proposition 20). We also know that triangles GTK and KTD are similar (by Book VI, Prop. 8) and this implies
|
|
|
|
|
(1) |
Now consider the similar triangles TAG and TDH in the plane through O, G, and D, the axial plane. The triangles are similar because they each have a right angle and opposite vertical angles. This in turn implies
|
|
|
|
or |
 |
|
|
(2) |
Also in the axial plane are the pairs of similar triangles HDT and IEA, and BDT and BEA. From these we see that
|
|
|
|
|
(3) |
|
|
(4) |
Combining (3) and (4) we have
|
|
|
|
|
(5) |
Notice also that in triangle IEA the line OL bisects AE so it must also bisect AI, making IA = 2AL. Putting this together with (1) and (2) we have
|
|
(5) |
This might not look like an equation that we recognize, but if we let KT = y, the distance from the center of the ellipse to T be x, AB = 2a, and 2AL = p we have


 .
.
This does look like the equation of an ellipse.
Can You Really Derive Conic Formulae from a Cone? - Deriving the Symptom of the Obtuse-angled Cone
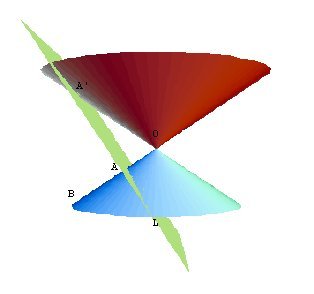
Next we consider the obtuse-angled cone with vertex O and a plane intersecting a generating line OB at a right angle at point A. The plane intersects the cone in the amblytome with diameter AG.
A dynamic view of this construction will be helpful in what follows.
[In order to open the dynamic view in a new window to allow you to show the text and the derivation side-by-side, right click or Ctrl-click on the link.]
 |
 |
Consider an arbitrary ordinate (i.e. y value) NP constructed on the axis at N. We wish to determine the relationship between NP and AN, that is, the symptom of the conic. The ordinate NP is located in a horizontal plane that cuts the cone in the circle with diameter BC. In this horizontal plane construct the segments BP and CP, which results in a right triangle inscribed in a semicircle. (The triangle is right by Elements, Book III, Proposition 20). We also know that triangles BNP and PNC are similar (by Book VI, Prop. 8) and this implies
|
|
|
|
|
(1) |
Now consider the similar triangles NAB and NCG in the axial plane plane through O, B, and C. The triangles are similar because they each have a right angle and opposite vertical angles. This in turn implies
|
|
|
|
or |
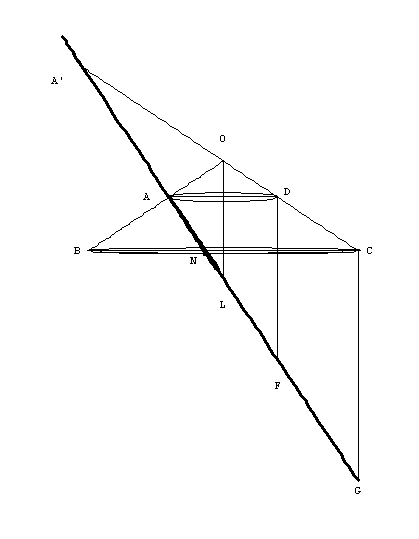 |
|
|
(2) |
Combining (1) and (2) we have
|
|
(3) |
In the axial plane we also have similar triangles GCN and FDA, because they each have a right angle and they have another equal angle since AD is parallel to NC. (See Elements Book I, Prop. 29, a very famous proposition indeed. Follow the link to see why.) These similar triangles give us:
|
|
|
|
|
(4) |
Finally, in the same axial plane are the similar triangles A'NC and A'AD. The triangles are similar because AD is parallel to NC in triangle A'NC (see for example, Elements Book VI, Prop. 2). From this we have
|
|
|
|
|
|
|
|
(5) |
Rewriting (5) as  and combining with (3) yields
and combining with (3) yields
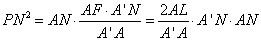 ,
,
using the fact that AF = 2AL.
Just as in the last section, we can make this look more like the modern equation of a hyperbola by substituting x = AN, y = NP, 2a = AA', and p = 2AL. This gives us
 ,
,
which can be rewritten as the modern form of a hyperbola. (Do you see how?)
Can You Really Derive Conic Formulae from a Cone? - Conic Sections of Apollonius - Introduction
Little is known of the life of Apollonius. The information we have is from his own writings and, once again, from Eutocius, in his work Commentary on Apollonius' Conics. Apollonius says of his work Conics,
Of the eight books the first four belong to a course in the elements. The first book contains the generation of the three sections and of the opposite branches, and the principal properties in them worked out more fully and universally than in the writings of others [1, p. 603].
Eutocius illuminates this further by stating
Apollonius of Perga proved generally that all the sections can be obtained in any cone, whether right or scalene, according to different relations of the plane to the cone [15, p. 279].
Indeed, Apollonius redefined the cone:
If from a point a straight line is joined to the circumference of a circle which is not in the same plane with the point, and the line is produced in both directions, and if, with the point remaining fixed, the straight line being rotated about the circumference of the circle returns to the same place from which it began, then the generated surface composed of the two surfaces lying vertically opposite one another, each of which increases indefinitely as the generating straight line is produced indefinitely, I call a conic surface, and I call the fixed point the vertex, and the straight line drawn from the vertex to the center of the circle the axis [1, p. 604].
Above: Drag point B to generate a nappe of the cone
Compare this with Euclid's definition of a cone on page 4.
Unlike earlier geometers who intersected planes at right angles to different shaped cones, Apollonius varied the plane, not the cone. The angle of intersection of the plane to the cone determined the conic. Let's see how this generates the three conic sections:
Parabola (plane slices the cone at a right angle)
Right click and drag to change the viewing angle.
Ellipse (plane slices the cone at an acute angle)
Right click and drag to change the viewing angle.
Hyperbola (plane slices the cone at an obtuse angle)
Right click and drag to change the viewing angle.
The Conics is a tour de force of information about conic sections. It would take us too far afield to discuss all of its wonderful propositions, many of which today require the aid of calculus for proof. The interested reader can read Apollonius's own account of his work from his introduction to Book I. In this work Apollonius gives us the names "parabola," ellipse," and "hyperbola," and we will look at how he derived the symptom of each of these conics in the following sections.
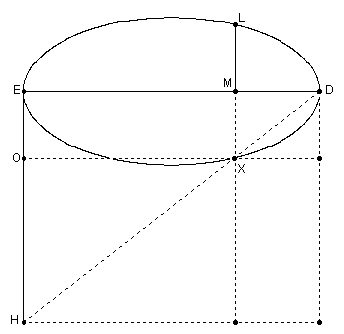
Can You Really Derive Conic Formulae from a Cone? - Deriving the Symptom of the Parabola
Apollonius, Conics, Book I, Proposition 11
If a cone is cut by a plane through its axis, and also cut by another plane cutting the base of the cone in a straight line perpendicular to the base of the axial triangle, and if further the diameter of the section is parallel to one side of the axial triangle, then any straight line which is drawn from the section of the cone to its diameter parallel to the common section of the ccutting plane and of the cone's base, will equal in square the rectangle contained by the straight line cut off by it on the diameter beginning from the section's vertex and by another straight line which has the ratio to the straight line between the angle of the cone and the vertex of the section that the square on the base of the axial triangle has to the rectangle contained by the remaining two sides of the triangle. And let such a section be called a parabola (παραβολή).
Consider the cone with vertex A and a plane through the axis intersecting the cone. This plane intersects the cone in the axial triangle ABC, where BC is the diameter of the base circle of the cone.
 |
 |
 The parabola is like the section of a right-angled cone (orthotome); if the cutting plane is orthogonal to a side of the axial triangle, it must also be parallel to the other side of the axial triangle (for right-angled cones). For Apollonius, the parabola is generated by a plane cutting one side of the axial triangle such that it is parallel to the other side. This works for all cones in general, but we illustrate here with a right circular cone. This has the added advantage of matching the derivation of the section of a right-angled cone that we skipped in Section 2a. This derivation and those for the ellipse and the hyperbola essentially follow those done in [11, pp. 119-121].
The parabola is like the section of a right-angled cone (orthotome); if the cutting plane is orthogonal to a side of the axial triangle, it must also be parallel to the other side of the axial triangle (for right-angled cones). For Apollonius, the parabola is generated by a plane cutting one side of the axial triangle such that it is parallel to the other side. This works for all cones in general, but we illustrate here with a right circular cone. This has the added advantage of matching the derivation of the section of a right-angled cone that we skipped in Section 2a. This derivation and those for the ellipse and the hyperbola essentially follow those done in [11, pp. 119-121].
A dynamic view of this construction will be helpful in what follows.
 |
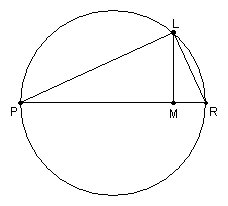 |
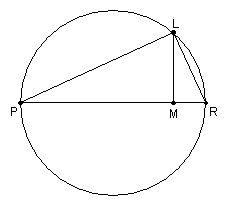
Consider an arbitrary ordinate (i.e. y value) ML constructed on the axis at M. We wish to determine the relationship between ML and EM, that is, the symptom of the conic. The ordinate ML is located in a horizontal plane that cuts the cone in the circle with diameter PR. In this horizontal plane construct the segments PL and LR, which results in a right triangle inscribed in a semicircle. As we have seen before, by similar triangles this implies
|
|
|
|
|
(1) |
Next Apollonius constructs a segment EH perpendicular to EM such that
|
|
(2) |  |
How is this possible? All the lengths EA, BC, BA, and AC are known. He is simply finding the point H that makes the ratio true. Now why Apollonius does this is an other story. Wait and see.
Now consider some triangles in the axial plane, namely ABC, APR, and EPM. These triangles are all similar, using the usual properties of parallel lines (see previous derivations for details). From the similarity we have
|
|
(3) |
|
and |
 |
|
|
(4) |
Combining (2), (3), and (4) gives us
|
|
(5) |
Also, in triangle APR, since EM is parallel to AR we know by Elements Book VI, Prop. 2 that
|
|
(6) |
Substituting (6) into (5) yields
|
|
(7) |
It is clear that
|
|
so combining this with (7) gives us
|
|
Recall from (1) that ML2 = PM.MR, therefore ML2 = EH.EM.
In this form we can understand Apollonius' use of the word parabola for this section. He has proven that the square on ML is equal to a rectangle applied (paraboli) to a line EH with a width equal to EM. This is based on the idea of application of areas, a Greek technique used to deal with multiplication and division of lengths and areas.
Finally, if we let ML be y, EM be x, and EH be p, we have a standard equation for a parabola, y2 = px.
Notice once again that all that was necessary to derive the symptom of the parabola was a knowledge of similar traingles. We will see this again as we derive the symptom of the next conic section, the ellipse.
Can You Really Derive Conic Formulae from a Cone? - Deriving the Symptom of the Ellipse
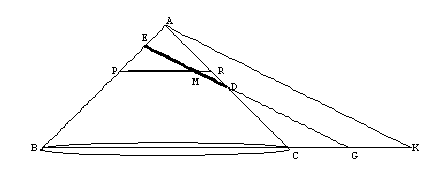
Apollonius, Conics, Book I, Proposition 13
If a cone is cut by a plane through its axis, and also cut by another plane on the one hand meeting both sides of the axial triangle, and on the other extended neither parallel to the base nor subcontrariwise, and if the plane the base of the cone is in, and the cutting plane meet in a straight line perpendicular either to the base of the axial triangle or to it produced, then any straight line which is drawn from the section of the cone to the diameter of the section parallel to the common section of the planes, will equal in square some area applied to a straight line to which the diameter of the section has the ratio that the square on the straight line drawn from the cone's vertex to the triangle's base parallel to the sections's diameter has to the rectangle contained by the intercepts of this straight line (on the base) from the sides of the triangle, an area having as breadth the straight line cut off on the diameter beginning from the section's vertex by this straight line from the section to the diameter, and deficient (έλλειπου) by a figure similar and similarly situated to the rectangle contained by the diameter and parameter. And let such a section be called an ellipse (έλλειψις). We will still consider the cone with vertex A and a plane through the axis intersecting the cone. This plane intersects the cone in the axial triangle ABC, where BC is the diameter of the base circle of the cone.
 |
 |
 To generate the ellipse the cutting plane must intersect both sides of the axial triangle. Once again this works for all cones in general, but we illustrate here with a right circular cone.
To generate the ellipse the cutting plane must intersect both sides of the axial triangle. Once again this works for all cones in general, but we illustrate here with a right circular cone.
A dynamic view of this construction will be helpful in what follows.
 |
 |
Consider an arbitrary ordinate (i.e. y value) ML constructed on the axis at M. We wish to determine the relationship between ML and EM, that is, the symptom of the conic. The ordinate ML is located in a horizontal plane that cuts the cone in the circle with diameter PR. In this horizontal plane construct the segments PL and LR, which results in a right triangle inscribed in a semicircle. As we saw before in the case of the parabola, by similar triangles this implies
|
|
|
|
|
(1) |
Apollonius next constructs a segment EH, perpendicular to DE, such that
|
|
(2) |  |
where AK is parallel to ED. [As in the previous section, all the lengths DE, AK, BK, and KC are known. He is simply finding the point H that makes the ratio true.]
Notice in the figure that triangles DEH and DMX are similar. This implies that
|
|
(3) |
where the first equality is due to the similarity, and the second one is due to the fact that MX = EO. Next, consider the cone diagram carefully (a different viewpoint is below). The triangles ABK, EBG, and EPM in the axial plane are all similar (parallel lines), and also the triangles ACK, DCG, and DMR are all similar (do you see why?). From these two sets of similar triangles we have
|
|
(4) |
|
and |
 |
|
|
(5) |
Combining (2), (4), and (5) gives us
|
|
(6) |
Now compare (3) and (6) and notice that they imply PM . MR = EM . EO. However, from (1) we have ML2 = PM . MR, so together we have ML2 = EM . EO.
Taking another look at our ellipse, notice that triangles DEH and XOH are similar. This implies
|
|
|
|
|
 |
|
|
(7) |
Notice that EO = EH - HO, so ML2 = EM . EO becomes, using (7),
|
|
(8) |
In this form we can understand Apollonius' use of the word ellipse for this section. He has proven that the square on ML is equal to a rectangle applied to a line HE with a width equal to EM and deficient (ellipsis) by a rectangle similar to one contained by ED and HE.
Equation (8) is also the form that will enable us to see this as the modern form of an ellipse. Let y = ML, x = EM, p = HE, and ED = 2a. Substituting into (8) we have
|
|
Can this be written in the standard form of an ellipse? Complete the square and see.
In the next section we derive the symptom of the hyperbola. The derivation follows that of this section. You will notice very little difference between the two until the very end. In Apollonius's Conics, propositions concerning the ellipse and the hyperbola are frequently proven together, due to their similarities.
Can You Really Derive Conic Formulae from a Cone? - Deriving the Symptom of the Hyperbola
Apollonius, Conics, Book I, Proposition 12
If a cone is cut by a plane through its axis, and also cut by another plane cutting the base of the cone in a straight line perpendicular to the base of the axial triangle, and if the diameter of the section produced meets one side of the axial triangle beyond the vertex of the cone, then any straight line which is drawn from the section to its diameter parallel to the common section of the cutting plane and of the cone's base, will equal in square some area applied to a straight line to which the straight line added along the diameter of the section and subtending the exterior angle of the triangle has a ratio that the square on the straight line drawn from the cone's vertex to the triangle's base parallel to the section's diameter has to the rectangle contained by the sections of the base which this straight line makes when drawn, this area having as breadth the straight line cut off on the diameter beginning from the section's vertex by this straight line from the section to the diameter and exceeding (ύπερβάλλου) by a figure (είδος), similar and similarly situated to the rectangle contained by the straight line subtending the exterior angle of the triangle and by the parameter. And let such a section be called an hyperbola (ύπερβολή).
We will once again consider the cone with vertex A and a plane through the axis intersecting the cone. This plane intersects the cone in the axial triangle ABC, where BC is the diameter of the base circle of the cone. To generate the hyperbola the cutting plane must intersect only one side of the axial triangle but also both "top" and "bottom" of the "double cone." As before this works for all cones in general, but we illustrate here with a right circular cone.
A dynamic view of this construction will be helpful in what follows.
 |
 |
Consider an arbitrary ordinate (i.e. y value) ML constructed on the axis at M. We wish to determine the relationship between ML and EM, that is, the symptom of the conic. The ordinate ML is located in a horizontal plane that cuts the cone in the circle with diameter PR. In this horizontal plane construct the segments PL and LR, which results in a right triangle inscribed in a semicircle. As we saw before in the case of the parabola, by similar triangles this implies
|
|
|
|
|
(1) |
As with the ellipse, Apollonius next constructs a segment EH, perpendicular to DE, such that
|
, |
(2) |
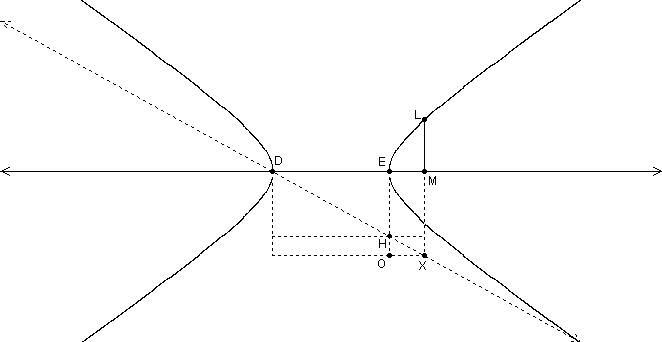
where AK is parallel to ED. [As before, all the lengths DE, AK, BK, and KC are known. He is simply finding the point H that makes the ratio true.]
Notice in the figure that triangles DEH and DMX are similar. This implies that
|
|
(3) |
where the first equality is due to the similarity, and the second one is due to the fact that MX = EO. Next, consider the cone diagram carefully (a different viewpoint is below). The triangles ABK, EBG, and EPM in the axial plane are all similar (parallel lines), and also the triangles ACK, DCG, and DMR are all similar (do you see why?). From these two sets of similar triangles we have
|
|
(4) |
|
and |
 |
|
|
(5) |
Combining (2), (4), and (5) gives us
|
|
(6) |
Now compare (3) and (6) and notice that they imply PM . MR = EM . EO. However, from (1) we have ML2 = PM . MR, so together we have ML2 = EM . EO.
Taking another look at our hyperbola, notice that triangles DEH and XOH are similar. This implies
|
|
|
|
|
|
|
|
(7) |
Here is where the hyperbola derivation changes from that of the ellipse. Notice now that EO = EH + HO, so ML2 = EM . EO becomes, using (7),
|
|
(8) |
From this expression comes Apollonius' use of the word hyperbola for this section. He has proven that the square on ML is equal to a rectangle applied to a line HE with a width equal to EM and exceeding (yperboli) by a rectangle similar to one contained by ED and HE.
Equation (8) is also the form that will enable us to see this as the modern form of a hyperbola. Let y = ML, x = EM, p = HE, and ED = 2a. Substituting into (8) we have
|
|
Can this be written in the standard form of a hyperbola? Again, it is up to you to try it.
With little more than a good grasp of similar triangles, we have derived the equations of the conic sections from the actual slices of cones. Apollonius's contemporaries called him "the Great Geometer" for his work with the conics. If you have made it this far, you at least deserve a hearty congratulations! Now what?
Can You Really Derive Conic Formulae from a Cone? - Where Can You Go From Here?
There are many wonderful and useful properties of conic sections; you are no doubt familiar with parabolic mirrors, elliptical "whispering rooms," and the like. Who first discovered these properties? Did Archimedes really use properties of conic sections to start enemy ships on fire? There is much more to investigate, but we must end our story here for now. You could dive right in and begin to investigate the wonders of Apollonius' Conics for yourself in [1] and [2]. Be aware that Apollonius is rough going, so you may want to start with a book on the history of mathematics, of which Katz [11] is the best. For a readable work on Archimedes' use of conic sections, check out [13]. For a look at conic sections from the point of view of geometric transformations, try [3]. Conic sections played an important role in Newton's theory of planetary motion in his Philosophia Naturalis Principia Mathematica [12]. Of course Newton's Principia is also very tough reading, so you might want to check out Dana Densmore's book [6], which stays true to the style of Newton's work, and contains plenty of material on conic sections; or Chandrasekhar's book [4], which uses modern mathematics to investigate the Principia. If all of this sounds intimidating, crack open a calculus book. They usually have a chapter on conic sections, where many of their useful properties are derived. A good calculus book with a historical spirit is Hahn's text [7].
In any case, there is much more to learn about conic sections, and why not learn it from the masters themselves? Good luck!
Can You Really Derive Conic Formulae from a Cone? - References
- Apollonius of Perga. Conics Books I-III, translated by R. Catesby Taliaferro, in Great Books of the Western World, Vol. 11, Chicago: Encyclopedia Britannica, 1952. Revised Edition, edited by Dana Densmore, Santa Fe: Green Lion Press, 2000. Book IV, translated by Michael Fried, Santa Fe: Green Lion Press, 2002.
- Apollonius. Conics Books V to VII, Edited with Translation and Commentary by G. J. Toomer, New York: Springer-Verlag, 1990.
- Brannan, David A., Matthew F. Esplen, and Jeremy J. Gray. Geometry, New York: Cambridge University Press, 1999.
- Chandrasekhar, Subrahmanyan. Newton's Principia for the Common Reader, New York: Oxford University Press, 1995.
- Coolidge, Julian Lowell. A History of the Conic Sections and Quadric Surfaces, Oxford: Clarendon Press, 1945.
- Densmore, Dana. Newton's Principia: The Central Argument, Santa Fe, NM: Green Lion Press, 1996.
- Hahn, Alexander. Basic Calculus: From Archimedes to Newton to its Role in Science, New York: Springer Verlag, 1998.
- Heath, Thomas. A History of Greek Mathematics, Vol. 1, New York: Dover Publications, 1981.
- Heath, Thomas. A History of Greek Mathematics, Vol. 2, New York: Dover Publications, 1981.
- Heath, Thomas. The Thirteen Books of the Elements, Vol. 1, New York: Dover Publications, 1956.
- Katz, Victor. A History of Mathematics: An Introduction, 2nd ed., Reading, MA: Addison-Wesley, 1998.
- Newton, Isaac. The Principia, Mathematical Principles of Natural Philosophy, a new translation by I. Bernard Cohen and Anne Whitman, Berkeley, CA: University of California Press, 1999.
- Stein, Sherman. What Did Archimedes Do Besides Cry Eureka?, Washington, D.C.: Mathematical Association of America, 1999.
- Thomas, Ivor. Selections Illustrating the History of Greek Mathematics, Vol. 1, Cambridge, MA: Harvard University Press, 1998.
- Thomas, Ivor. Selections Illustrating the History of Greek Mathematics, Vol. 2, Cambridge, MA: Harvard University Press, 1998.
 or
or
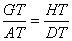

 or
or and
and .
. or
or .
.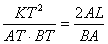 .
.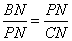 or
or

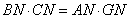
 .
. or
or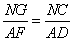 .
. or
or and combining with (4)
and combining with (4)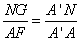 .
.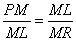 or
or
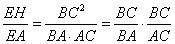

 .
. .
.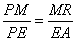 .
. .
. ,
,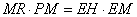 .
.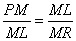 or
or .
.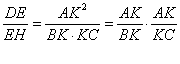 ,
,

 .
. .
.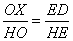

 .
.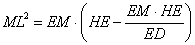 .
. .
. or
or .
.


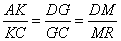 .
. .
.

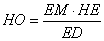 .
. .
. .
.