Benjamin Banneker's Trigonometry Puzzle
The mathematical puzzles of Benjamin Banneker (1731-1806) have been of interest since he first produced them in the last half of the 18th century and the early years of the 19th. By the age of 21, he was a hero in the territory of Maryland.* Banneker began his life-changing studies of astronomy and mathematics about 1788, the year Maryland joined the Union, when he was lent some books by his friend, the surveyor George Ellicott. Three of these are known: Charles Leadbetter's Astronomy: Or the True System of the Planets Demonstrated (1727); James Ferguson's Astronomy Explained Upon Sir Isaac Newton's Principles, and Made Easy to Those Who Have Not Studied Mathematics (1761); and a book (in Latin) which Ellicott gave his bride as a wedding present.
In one of the puzzles, “Trigonometry,” Banneker demonstrates his knowledge of logarithms as he presents his solution. The question arises as to what book of logarithmic tables could Banneker have been using. The trigonometry page is reproduced here by permission of The Maryland Historical Society, Baltimore, Maryland, where Banneker’s Astronomical Journal 1798, is kept, less than 10 miles from where it was written.

This puzzle also demonstrates Banneker’s humor, for after he gives a generalization of his plan, he creates a specific problem, solves it using logarithms, and sums it all up by implying it could have been done far more simply. He provides us with a neat lesson on reflecting back upon solutions.
________________________
*Banneker’s life can be explored in detail in Silvio Bedini’s Benjamin Banneker, the First African-American Man of Science, Baltimore: Maryland Historical Society, 1999.
Benjamin Banneker's Trigonometry Puzzle - Introduction
The mathematical puzzles of Benjamin Banneker (1731-1806) have been of interest since he first produced them in the last half of the 18th century and the early years of the 19th. By the age of 21, he was a hero in the territory of Maryland.* Banneker began his life-changing studies of astronomy and mathematics about 1788, the year Maryland joined the Union, when he was lent some books by his friend, the surveyor George Ellicott. Three of these are known: Charles Leadbetter's Astronomy: Or the True System of the Planets Demonstrated (1727); James Ferguson's Astronomy Explained Upon Sir Isaac Newton's Principles, and Made Easy to Those Who Have Not Studied Mathematics (1761); and a book (in Latin) which Ellicott gave his bride as a wedding present.
In one of the puzzles, “Trigonometry,” Banneker demonstrates his knowledge of logarithms as he presents his solution. The question arises as to what book of logarithmic tables could Banneker have been using. The trigonometry page is reproduced here by permission of The Maryland Historical Society, Baltimore, Maryland, where Banneker’s Astronomical Journal 1798, is kept, less than 10 miles from where it was written.

This puzzle also demonstrates Banneker’s humor, for after he gives a generalization of his plan, he creates a specific problem, solves it using logarithms, and sums it all up by implying it could have been done far more simply. He provides us with a neat lesson on reflecting back upon solutions.
________________________
*Banneker’s life can be explored in detail in Silvio Bedini’s Benjamin Banneker, the First African-American Man of Science, Baltimore: Maryland Historical Society, 1999.
Benjamin Banneker's Trigonometry Puzzle - Explanation of Banneker's Solution
It is clear that Banneker is using the Law of Sines**: In a triangle, the ratios of the sine of an angle to the length of its opposite side are equal. Where Banneker writes in his proportion, "logarithm base 26" or "logarithm of the hypotenuse," he is anticipating the use of logarithms for the computation. Banneker understood, as his calculations correctly show, that the ratios involved are the sine of an angle to the side opposite, not to the log of the side. In what follows, all angles are expressed in degrees.
I. To find the hypotenuse, Banneker used the Law of Sines: sin C/ c = sin B/ b.
"Sine complement of the angle at A," is sin 60, the sine of the angle complementary to angle A. If x is the length of the hypotenuse, then sin 60/ 26 = sin 90/ x and x = 26 sin 90/ sin 60. Taking logarithms, we have
log x = log 26 + log sin 90 - log sin 60
and, substituting values from a suitable set of tables,
log x = 1.41497 +10 – 9.93753 = 1.47744.
Notice that, for reasons we shall see later, log sin 90 = Log 1010 = 10. We now find x as the antilogarithm of 1.47744, which is very close to 30. It is unlikely that Banneker would have had access to tables of antilogarithms, a late eighteenth century invention, but would simply have used his table of logarithms in reverse.
II. To find the remaining side, Banneker uses the Law of Sines again: sin C/ c = sin A/ a. If x is the length of the side perpendicular to the base then sin 60/ 26 = sin 30/ x, and x = 26 sin 30/sin 60. Taking logarithms we get
log x = log 26 + log sin 30 - log sin 60
and, again substituting values from tables,
log x = 1.41497 + 9.69897 - 9.93753 = 1.7641.
Again, x is the antilogarithm of 1.17643, which is very close to 15.
________________________
**Beatrice Lumpkin’s comments on Banneker’s Trigonometry Puzzle were used for the printed program at a Benjamin Banneker Association session at the NCTM meeting in 1992. See also her article, “From Egypt to Benjamin Banneker: African Origins of False Position Solutions,” in Vita Mathematica: Historical Research and Integration with Teaching, Ronald Calinger, Ed., Washington: MAA, 1996, pp. 279-289. The article is a shortened version of a paper presented at the Quadrennial Meeting of the International Study Group on the Relations Between History and Pedagogy of Mathematics (HPM) at the University of Toronto, August, 1992.
Benjamin Banneker's Trigonometry Puzzle - Which Logarithm Tables Were Available in Maryland in 1798?
When Graham Jagger, a tutor at The Open University with a particular interest in logarithms was sent the puzzle in January 2004, he used historical detective work to find the tables that Banneker probably used. The logarithms used above are to base 10; i.e. Briggsian, or common, logarithms. Briggs’s logarithm tables were more or less freely copied by later printers and formed the basis of all subsequent tables until the beginning of the nineteenth century.
The following tables, all derived from those of Briggs, may have been available in the new State of Maryland in 1788 and hence could have been used by Banneker in 1798, the year of the page in his journal:
|
Henry Briggs |
Arithmetica Logarithmica |
1624 |
London |
Logarithms of numbers from 1 to 20,000 and from 90,000 to 100,000 (to 14 figures). |
|
Henry Briggs |
Arithmetica Logarithmica |
1628 |
Gouda |
A second edition of the above published by Adrian Vlacq, who calculated the additional logarithms from 20,000 to 90,000 (to 10 figures), and the logarithms of sines, tangents and secants (to 10 figures). |
|
Henry Briggs |
Trigonometria Britannica |
1633 |
London |
Logarithms of sines and tangents (to 14 decimal places). |
|
John Newton |
Tabulæ Mathematicæ |
1654 |
London |
Logarithms of numbers and trigonometric functions taken from Briggs (to 6 decimals). |
|
William Oughtred |
Trigonometria |
1657 |
London |
Logarithms of numbers (to 7 decimals) and trigonometric functions (to 6 decimals) taken from Briggs. |
Benjamin Banneker's Trigonometry Puzzle - Conclusion
Because the logarithms in the worked examples are all to five decimal places, they do not seem to fit with any of the tables on page 3. However, it is instructive to examine the format of Briggs’s logarithms from Vlacq’s edition of 1628:
|
log 26 |
1, 41497, 33480 |
|
log(sin 30) |
9, 69897, 00043 |
|
log(sin 60) |
9, 93753, 06317 |
|
log(sin 90) |
10, 00000, 00000 |
Briggs himself defined the first (left-most) comma as standing in for the decimal point; subsequent commas, dividing the figures into groups of five, are merely placeholders to guide the eye. The logarithms in the worked example can be simply obtained merely by discarding the five right-most digits from the values given in the table. (As it happens, with the particular numbers chosen by Banneker, no rounding issue arises by the simple truncation of the tabular values.) It seems highly probable, therefore, that the logarithms used in the example did indeed come from the second edition of Briggs’s Arithmetica Logarithmica (Valcq, 1628), or its derivative, the Logarithmicall Arithmetike of 1634.
At the beginning of the seventeenth century, trigonometric functions were defined as follows:
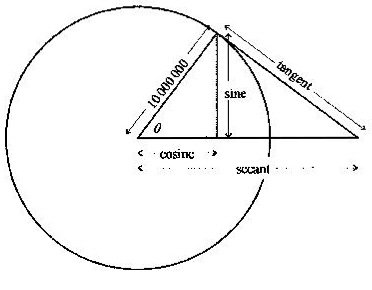
The radius of the circle was chosen so that the function values could be represented as integers to any desired degree of accuracy. Napier chose a radius of 107 (shown here); Briggs chose a radius of 1010. So, for Briggs, the sine of 90° (the whole sine or sinus totus) was 1010 and its (Briggsian) logarithm is, therefore, simply 10 ... and the logarithms of all the sines in the first quadrant are positive. In modern trigonometry, the radius is taken as unity – a convention unknown much before 1800 – so the sines of the angles in the interval [0°, 90°] are less than unity and their logarithms are, consequently, negative. The fact that the logarithms of sines in Briggs’s table are positive therefore arises naturally from the way in which the sine function was then defined.
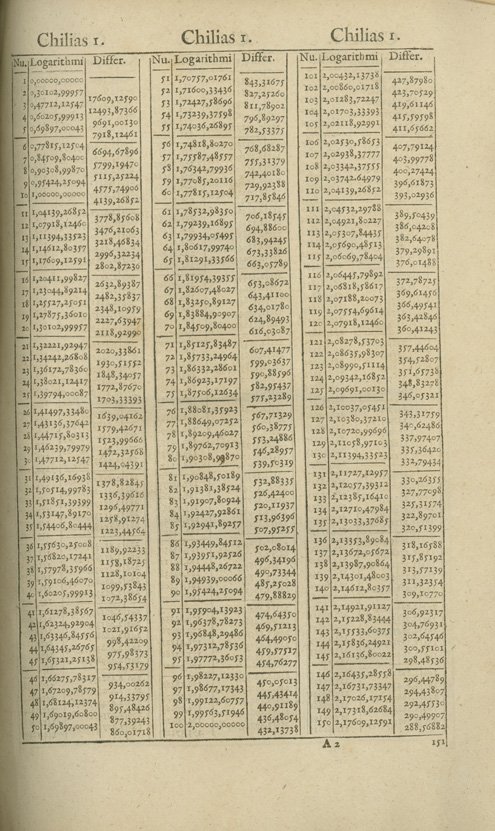
Image of a logarithm table from Briggs’s Arithmetica Logarithmica (Valcq, 1628), courtesy of Brenda Corbin, United States Naval Observatory, Washington, DC.