Van Schooten's Ruler Constructions
Editor's note: The article, "Van Schooten's Ruler Constructions," by C. Edward Sandifer, was originally published in the inaugural issue of Convergence in April of 2004. Ten years after its original appearance, in 2014, Convergence is pleased to restore and republish this article about the Dutch mathematician Frans van Schooten, his work in geometry, and how this work can be used in the classroom.
Introduction
Frans van Schooten (1615-1660) was one of those mathematicians on whose shoulders the giants stood. Perhaps none of van Schooten’s mathematics was truly original, yet he provided an essential link for at least four great and original mathematicians, François Vieté (1540-1603), René Descartes (1596-1650), Christian Huygens (1629-1695) and Isaac Newton (1643-1727).

Frans van Schooten (Source: Convergence Portrait Gallery)
Van Schooten was born, studied, worked and died in Leiden, Netherlands. There, in 1637, he met Descartes, who was visiting, and was thus introduced to the mathematical circle of Marin Mersenne. In 1643, he joined his father as an assistant professor in the engineering school at the University of Leiden and succeeded his father two years later. He held that post until his death in 1660.
During that career, van Schooten seems to have published four books. The first, and most forgettable, was a collection of trigonometric tables, published in 1645. This book, with the typically long 17th Century title, Table de sinus, tangentes et secantes ad radium 10,000,000 : Avec une methode de resoudre très-facilement par leur moyen tous les triangles rectilignes & spheriques, is a little unusual in that the title changes language from Latin to French halfway through. At the time, decimal fractions were not in wide use, so van Schooten’s tables were in the old style. They gave the measurements for the sine, tangent and secant on a circle of radius 10,000,000 rather than on a circle of radius 1, as we do today. Thus, the sin 90°, also called the “total sine” was given as 10,000,000, and the sine of 45° was 7,071,068 and not 0.7071068, as we would use today. Anyone using these tables would use rules of proportion to make any necessary conversions. Schooten probably wrote only the text that described how to use these tables, and the tables were probably just a reprint of tables that had already been published before.
Van Schooten’s first important book was his Collected Works of François Vieté, published in 1646. This made Vieté’s algebraic notations and techniques available to a wider audience, and also established van Schooten’s fame in the mathematical community.
Van Schooten is best known for translating Descartes’ Geometria into Latin and publishing it, with some commentaries. The first edition of this translation appeared in 1649, a year before Descartes’ death. It is said that Descartes opposed the project, but the copyright laws of the times did not allow him to prevent its publication. Descartes had written the Geometria as an appendix to his Discourse on the Method in 1638. It had been written in French. At the time, virtually all scholars could read and write Latin, but relatively few could read French, so Descartes’ groundbreaking work was not very widely available. Van Schooten’s Latin translation made Descartes’ Geometria available to a much wider scholarly audience, while his commentaries, along with those of Florimond DeBeaune, enabled people to understand and use Descartes’ often deliberately sketchy discoveries and ideas.
The 1649 edition of Descartes’ Geometria was so successful that van Schooten recruited three more distinguished commentators, Johann Hudde, Jan de Witt and Henri Heuraet and expanded the commentaries to two volumes, published in 1659 and 1661. Just five years later, a young Isaac Newton, who could read Latin but not French, read Hudde’s commentaries about methods for finding the slopes of lines tangent to curves. He worked pages and pages of examples before he came upon the general principles of differential and integral calculus and made all of Hudde’s work obsolete. Thus, van Schooten was the editor who carried Descartes’ ideas, through Hudde and others, to Isaac Newton, at almost exactly the time he needed those ideas to discover calculus.
Van Schooten’s commentaries on Descartes continued to be popular well after his death in 1660. There was a third edition, virtually identical to the second, published in 1683, and a fourth edition in 1694. The fourth edition included some new commentaries by Bernoulli.
Not all of van Schooten’s work was based on the works of others. Indeed, none of these three works, the tables, the collected works of Vieté, and the commentaries on Descartes, were very original, though they were quite important. However, between the first and second edition of the Descartes, van Schooten made his only foray into original work. In 1657, he published his Exercitationum mathematicarum libri quinque. As the title suggests, the work is divided into five “books” of about a hundred pages each.
Somehow, even in his master work, van Schooten arranged to be overshadowed by the work of others. Almost as an afterthought, van Schooten translated from Dutch an article by his student Christian Huygens. He included this as a 14 page appendix titled “De ratiocinis in ludo aleae.” As it turned out, this short article contained 14 propositions, the first theorems proved and published in the field of probability. These 14 pages by van Schooten’s student have proved far more important than the 520 pages that van Schooten himself wrote.
This is not to say the book itself is not interesting. In the next section, we provide an overview of van Schooten's Exercitationum mathematicarum libri quinque. For seven images from a copy of this text once owned by Hudde, see the Convergence article, "Mathematical Treasure: Frans van Schooten's Exercitationes mathematicae."
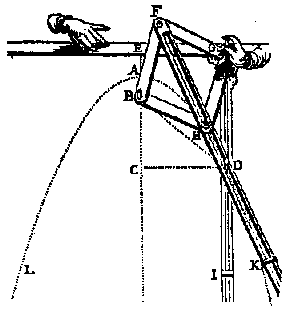
Parabola drawer from Book IV of van Schooten's Exercitationes mathematicae
Interested in using van Schooten's problems in your geometry class? Be sure to see Note to Teachers.
Next:
Van Schooten's Ruler Constructions - Introduction
Editor's note: The article, "Van Schooten's Ruler Constructions," by C. Edward Sandifer, was originally published in the inaugural issue of Convergence in April of 2004. Ten years after its original appearance, in 2014, Convergence is pleased to restore and republish this article about the Dutch mathematician Frans van Schooten, his work in geometry, and how this work can be used in the classroom.
Introduction
Frans van Schooten (1615-1660) was one of those mathematicians on whose shoulders the giants stood. Perhaps none of van Schooten’s mathematics was truly original, yet he provided an essential link for at least four great and original mathematicians, François Vieté (1540-1603), René Descartes (1596-1650), Christian Huygens (1629-1695) and Isaac Newton (1643-1727).

Frans van Schooten (Source: Convergence Portrait Gallery)
Van Schooten was born, studied, worked and died in Leiden, Netherlands. There, in 1637, he met Descartes, who was visiting, and was thus introduced to the mathematical circle of Marin Mersenne. In 1643, he joined his father as an assistant professor in the engineering school at the University of Leiden and succeeded his father two years later. He held that post until his death in 1660.
During that career, van Schooten seems to have published four books. The first, and most forgettable, was a collection of trigonometric tables, published in 1645. This book, with the typically long 17th Century title, Table de sinus, tangentes et secantes ad radium 10,000,000 : Avec une methode de resoudre très-facilement par leur moyen tous les triangles rectilignes & spheriques, is a little unusual in that the title changes language from Latin to French halfway through. At the time, decimal fractions were not in wide use, so van Schooten’s tables were in the old style. They gave the measurements for the sine, tangent and secant on a circle of radius 10,000,000 rather than on a circle of radius 1, as we do today. Thus, the sin 90°, also called the “total sine” was given as 10,000,000, and the sine of 45° was 7,071,068 and not 0.7071068, as we would use today. Anyone using these tables would use rules of proportion to make any necessary conversions. Schooten probably wrote only the text that described how to use these tables, and the tables were probably just a reprint of tables that had already been published before.
Van Schooten’s first important book was his Collected Works of François Vieté, published in 1646. This made Vieté’s algebraic notations and techniques available to a wider audience, and also established van Schooten’s fame in the mathematical community.
Van Schooten is best known for translating Descartes’ Geometria into Latin and publishing it, with some commentaries. The first edition of this translation appeared in 1649, a year before Descartes’ death. It is said that Descartes opposed the project, but the copyright laws of the times did not allow him to prevent its publication. Descartes had written the Geometria as an appendix to his Discourse on the Method in 1638. It had been written in French. At the time, virtually all scholars could read and write Latin, but relatively few could read French, so Descartes’ groundbreaking work was not very widely available. Van Schooten’s Latin translation made Descartes’ Geometria available to a much wider scholarly audience, while his commentaries, along with those of Florimond DeBeaune, enabled people to understand and use Descartes’ often deliberately sketchy discoveries and ideas.
The 1649 edition of Descartes’ Geometria was so successful that van Schooten recruited three more distinguished commentators, Johann Hudde, Jan de Witt and Henri Heuraet and expanded the commentaries to two volumes, published in 1659 and 1661. Just five years later, a young Isaac Newton, who could read Latin but not French, read Hudde’s commentaries about methods for finding the slopes of lines tangent to curves. He worked pages and pages of examples before he came upon the general principles of differential and integral calculus and made all of Hudde’s work obsolete. Thus, van Schooten was the editor who carried Descartes’ ideas, through Hudde and others, to Isaac Newton, at almost exactly the time he needed those ideas to discover calculus.
Van Schooten’s commentaries on Descartes continued to be popular well after his death in 1660. There was a third edition, virtually identical to the second, published in 1683, and a fourth edition in 1694. The fourth edition included some new commentaries by Bernoulli.
Not all of van Schooten’s work was based on the works of others. Indeed, none of these three works, the tables, the collected works of Vieté, and the commentaries on Descartes, were very original, though they were quite important. However, between the first and second edition of the Descartes, van Schooten made his only foray into original work. In 1657, he published his Exercitationum mathematicarum libri quinque. As the title suggests, the work is divided into five “books” of about a hundred pages each.
Somehow, even in his master work, van Schooten arranged to be overshadowed by the work of others. Almost as an afterthought, van Schooten translated from Dutch an article by his student Christian Huygens. He included this as a 14-page appendix titled “De ratiocinis in ludo aleae.” As it turned out, this short article contained 14 propositions, the first theorems proved and published in the field of probability. These 14 pages by van Schooten’s student have proved far more important than the 520 pages that van Schooten himself wrote.
This is not to say the book itself is not interesting. In the next section, we provide an overview of van Schooten's Exercitationum mathematicarum libri quinque. For seven images from a copy of this text once owned by Hudde, see the Convergence article, "Mathematical Treasure: Frans van Schooten's Exercitationes mathematicae."

Parabola drawer from Book IV of van Schooten's Exercitationes mathematicae
Interested in using van Schooten's problems in your geometry class? Be sure to see Note to Teachers.
Next:
Van Schooten's Ruler Constructions - Overview and Problem I
In this article, we mean to discuss the topics from Book II of van Schooten's Exercitationum mathematicarum libri quinque, but first it would be a good idea to look at the book as a whole.
Book I is a fairly standard review of arithmetic and ordinary geometry.
Book II contains the ruler constructions that we will get to later.
In Book III, van Schooten tries to reconstruct some of the works of Apollonius on plane loci. This was an important research topic of the time, and both Fermat and Descartes devoted a lot of effort to it as well. As usual, van Schooten is about 15 years late, though.
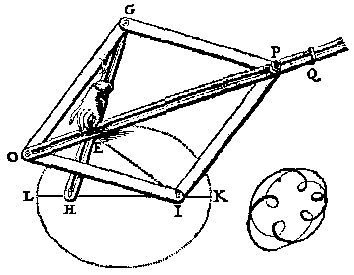
Ellipse drawer from Book IV of van Schooten's Exercitationes mathematicae
Book IV contains van Schooten’s best known work. Its title is “Organica conicarum sectionum”, or “Instruments of conic sections.” The word “organica” is more closely related to the organ as a musical instrument than to the “organic” we sometimes encounter in chemistry or agriculture. As the title suggests, the chapter describes a variety of beautiful instruments for drawing the various conic sections. One of several mechanisms for drawing a parabola is shown on the preceding page of this article, and another for drawing an ellipse is pictured here. All of the instruments are shown being operated by elegant disembodied hands, sometimes showing the cuffs of beautifully ruffled sleeves fashionable at the time. Several of the illustrations include beautiful and irrelevant doodles, like the rosette beside the ellipse machine. For animated versions of van Schooten's parabola and ellipse drawers, see Figures 2, 6, and 8 in the module "Curve Drawing Then and Now" in the Convergence article, "Historical Activities for the Calculus Classroom."
Finally, Book V is titled “Sectiones triginta miscellaneas”, or Thirty miscellaneous sections. In these sections, van Schooten carefully develops the combinatorial principles of counting. It is probably his best work, and it provides a complete foundation for the work of Huygens that follows in the appendix.
Then, van Schooten uses these new counting principles to re-discover the two new pairs of amicable numbers that Fermat and Descartes had discovered fifteen years earlier. Remember that a pair of numbers is amicable if the proper factors of one number add up to the other, and vice versa. For 2000 years, 284 and 220 were the only known pair of amicable numbers. Just a couple of years apart, Fermat and Descartes each discovered another pair. In fact, those two pairs had been discovered a couple of centuries earlier by Arab mathematicians. Van Schooten, of course, knew about the pairs that Fermat and Descartes had discovered, but his approach showed how both pairs could be discovered using the same method. It gave hope that more pairs could be discovered in the same way. Alas, the technique was a dead end, and no new amicable pairs would be discovered for another hundred years.
We return to Book II, “Constructio problematium simplicium geometricorum”, Solution of simple problems of geometry. Van Schooten gives us three postulates. One may
- connect two points with a straight line,
- extend a line, and
- copy a line onto another.
We might call these “ruler constructions”, because we are not allowed to use a compass in the geometric constructions. It might be more rigorous to call them “straightedge constructions,” because we are not allowed to use the instrument to measure anything.
Postulate 3 makes van Schooten’s ruler more powerful than Euclid’s ruler was. We are allowed to use our ruler to copy the length of one line segment onto another line. The postulate does not tell us how to do this, only that it is possible to do it. In practice, we can copy a segment by making a mark on the ruler.
Van Schooten gives us his ruler constructions as a series of ten problems, with solutions. For some problems, he gives two or more solutions. He begins with bisecting a given angle.
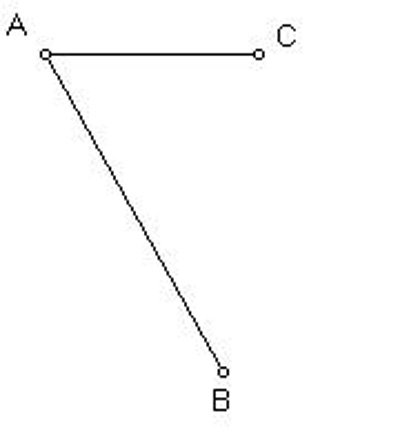
Problem I. Given a rectilinear angle BAC, to cut it into two equal pieces.
Next:
Details of first solution to Problem I
Quicker version of first solution to Problem I (verbatim translation of van Schooten’s solution)
Van Schooten's Ruler Constructions - Details of First Solution to Problem I
We repeat Problem I, trisecting a given angle.
Problem I. Given a rectilinear angle BAC, to cut it into two equal pieces.
The details of van Schooten's first solution to this problem are as follows.
|
Given the angle BAC, |
|
|
copy the segment AC onto the line AB to get the segment AD equal to AC. |
|
|
Likewise, copy the length AB onto the line AC, extended if necessary, to get the segment AF equal to AB. |
|
|
Now, draw the straight lines BC and DF, and let them intersect at the point G. |
|
|
Now, the line AG will cut the angle into two equal pieces. |
|
The sharp reader will notice that in this solution, we seem to assume that segment AC is shorter than segment AB. Though that can easily be circumvented, the solution will not quite work as given in the special case that AC equals AB. These issues do not seem to bother van Schooten at all.
Next:
Van Schooten's Ruler Constructions - Verbatim First Solution to Problem I
We repeat Problem I, trisecting a given angle.
Problem I. Given a rectilinear angle BAC, to cut it into two equal pieces.
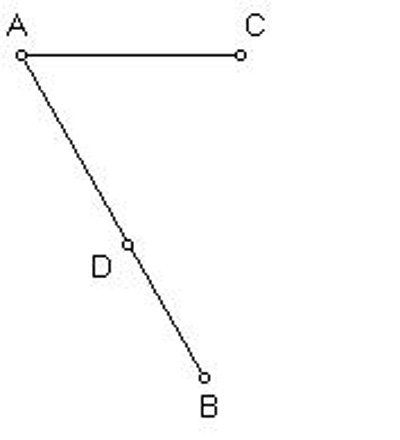
In the detailed version of the solution to Problem I given on the preceding page, we slightly misrepresented the given data. In fact, when van Schooten gives us the angle BAC, he seems to be assuming that AB is a segment, and that C is a segment with A as one of its endpoints. It could also be that B and C are both line segments, sharing A as an endpoint, and that the symbol B is also used to denote a point on the segment B. This seems to have no real consequence, but it is curious. Van Schooten’s words translate as follows.
Suppose that in the line AB points B and D are placed. and are placed on line AC so that AE equals AD, and E is a point further along AC so that EF equals DB; And draw straight lines BE, DF, which intersect at G. I say that the line AG cuts the angle BAC into two equal pieces.

Van Schooten also includes a proof of the correctness of each of his constructions, but we will generally leave those to the reader.
Next:
Van Schooten's Ruler Constructions - Second Solution to Problem I
Van Schooten offered a second solution to the problem of bisecting an angle BAC. He wrote:
Another way: Assuming the point B is in AB, find in CA, produced through A, the segments AD, DE, each equal to AB, and draw the straight line through the points E, B, and put on it BF equal to BE, and join AF. I say it bisects that angle BAC.
The proof of correctness of this construction may not be immediately obvious. As a hint, we suggest that a line from B to D might be useful.

Next:
Van Schooten's Ruler Constructions - Third Solution to Problem I
We repeat Problem I, trisecting a given angle.
Problem I. Given a rectilinear angle BAC, to cut it into two equal pieces.
Van Schooten wrote a third solution.
And another way. Assume, as before, AD equals AB, that BD are joined, and that BE equals BA. And from E through D an indefinitely long straight line is drawn. In that, if DF is put, equal to DE, and from F through H [sic: should be A] is drawn FA: I say that this bisects the angle BAC.
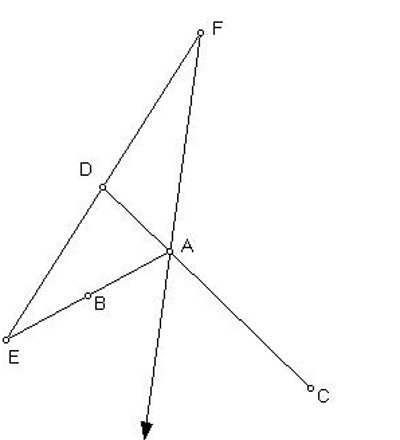
Next:
Van Schooten's Ruler Constructions - Fourth Solution to Problem I
We repeat Problem I, trisecting a given angle.
Problem I. Given a rectilinear angle BAC, to cut it into two equal pieces.
Van Schooten wrote a fourth solution.
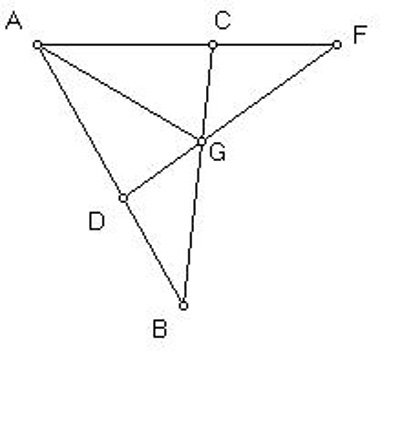
Again another way: Assume in AB the given point G, and from A is located in AC a line AF equal to AB; CA is produced to E so that EA is either larger or smaller than AB. Then produce BA from the point A and place a straight line AD equal to AE; and make through the points E, B and D, F straight lines EBG and DFG, which intersect at G. This done, if the straight line is drawn through AG, it will bisect that angle BAC.
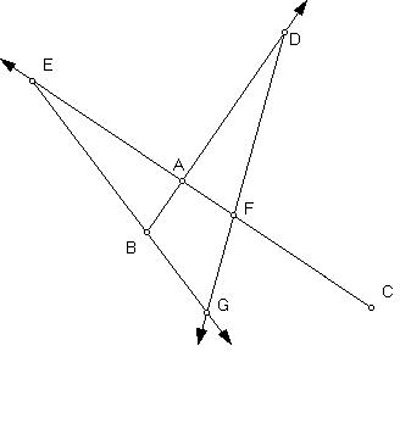
Van Schooten gives two diagrams, depending on whether EA is larger or smaller than AB. We give here the illustration taking EA larger than AB.
Next:
Van Schooten's Ruler Constructions - Problem II
Here is van Schooten's second problem and his first solution to it.
Problem II: Given a straight line with endpoints A, B, to bisect it.
Construction: Take any point C at random away from the line AB, and from A through C draw the indefinitely long line ACD, and locate on that line CD equal to the double of AC, and from D through B make a straight line. In that line, put BE equal to BD, and, joining C, E, I say it bisects AB at F.

Next:
Van Schooten's Ruler Constructions - Second Solution to Problem II
Van Schooten then presented a second solution to Problem II.
Problem II: Given a straight line with endpoints A, B, to bisect it.
Another way: Find, as before, away from AB, any point C, and draw from it through the points A and B straight lines CAD, CBE, and make AD equal to AC and BE equal to BC. Then join DB, AE, and let them intersect at F. I say that if FC is made, it will bisect AB at G.

Next:
Van Schooten's Ruler Constructions - Third Solution to Problem II
Finally, van Schooten presented a third solution to Problem II.
Problem II: Given a straight line with endpoints A, B, to bisect it.
Another way: Assume, as before, C is a point away from AB, and from B through C is drawn an indefinitely long line, and find on it CD equal to CB, and join it to A to form AD. Then in DA, assume DE equals DC and EF equals CB. [Here, van Schooten gives five illustrations, showing each of the following five cases: 1) DF = DA, 2) DF < DA, 3) DF > DA but DE < DA, 4) DE = DA, and 5) DE > DA. We illustrate case #2 only.)] Make BE, FC intersecting at G, then DGH cutting FB in H.
If now F falls on the point A, then the lines FB and AB coincide, and then H bisects it.
But if the point F falls beyond or within A, I say that if the line is drawn through the points C and H, it will bisect the line AB at I.

Next:
Van Schooten's Ruler Constructions - The Other Eight Problems
We now give the remaining eight of van Schooten’s ruler construction problems, with links to his solutions. The Note to Teachers gives ideas and advice about how to use any or all of van Schooten's ten problems, along with a set of trigonometry exercises based on a trig table from van Schooten's time, in class.
Problem III: Through a given point C draw a straight line parallel to a given straight line AB. Solution to Problem III
Problem IV: Above a given indefinitely long straight line, to construct a perpendicular. Solution to Problem IV
Note that we are not asked to construct this perpendicular at any particular place. All van Schooten asks is that the resulting line be perpendicular to the given line. Compare this problem with Problem V.
Problem V: Given an indefinitely long straight line AB and a point C on it, to draw a line CF which is perpendicular to the given straight line. Solution to Problem V
Problem VI: To a given straight line AB and at a given point C in that line, to construct an angle given ACI equal to a given rectilineal angle E. Solution to Problem VI
Problem VII: Given an indefinitely long line AB and a point C away from it, to draw CF which makes an angle with the given line AB which is equal to a given angle E. Solution to Problem VII
Problem VIII: Above a given straight line AB, to construct an equilateral triangle. Solution to Problem VIII
This particular problem is fairly important to van Schooten, since it is Proposition 1 of Book I of Euclid’s Elements.
Problem IX: Given a straight line AB, to extend it to G so that the total AG to the extreme GB has a given ratio C to D. Solution to Problem IX
Problem X: Given three straight lines AB, BC and AD, to find a fourth proportional DE, that is so that AB is to BC as AD is to DE. Solution to Problem X
Next:
Van Schooten's Ruler Constructions - Solution to Problem III
Problem III: Through a given point C draw a straight line parallel to a given straight line AB.
Construction: Draw from C through A an indefinitely long straight line and put on it AD equal to AC and from D through B make DBE. In that, place BE equal to BD and join CE. I say that it is parallel to AB.

Next:
Van Schooten's Ruler Constructions - Solution to Problem IV
Problem IV: Above a given indefinitely long straight line, to construct a perpendicular.
Construction: Conceive the given straight line as going through points A and B, and a perpendicular is to be constructed above it; make BC equal to AB [along the same line] and from B draw BD, making with AB any angle whatsoever, and locate D on that line so that it equals BA or BC, and draw the line from point D through point C. If in that line CF is made equal to CA, and in the line ABC, CE is made equal to CD, I say joining EF makes it be perpendicular to AB.
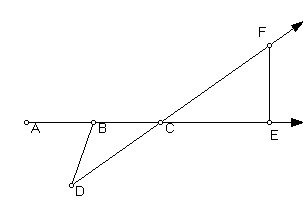
This may be van Schooten’s trickiest construction. The key to the proof of correctness is to note that the points A, C and D are all the same distance from B, so they lie on a circle centered at B and with AC as a diameter. This makes angle ADC a right angle. Now you only have to figure out why angle CEF is also a right angle.
Next:
Van Schooten's Ruler Constructions - Solution to Problem V
Problem V: Given an indefinitely long straight line AB and a point C on it, to draw a line CF which is perpendicular to the given straight line.
Construction: Draw, as in the previous problem, any perpendicular DE above AB, and then, from C, by the third, problem, draw a line CF parallel to that. It will be the one sought.
Next:
Van Schooten's Ruler Constructions - Solution to Problem VI
Problem VI: To a given straight line AB and at a given point C in that line, to construct an angle given ACI equal to a given rectilineal angle E.
Construction: Construct above DE by the 4th problem, a perpendicular DF, meeting EF at F, and put at the point C in AB a line CG equal to ED, and from G construct over AB, by the preceding problem a perpendicular GH: I say that GI equals DF, and joining CI, the angle ACI will equal the angle E.

Next:
Van Schooten's Ruler Constructions - Solution to Problem VII
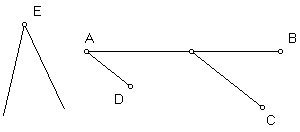
Problem VII: Given an indefinitely long line AB and a point C away from it, to draw CF which makes an angle with the given line AB which is equal to a given angle E.
Construction: To the point A in AB, construct, following the previous problem, and angle DAB, equal to E, and draw C, from the 3rd problem, line CF parallel to the line AD: I say the angle CFB is equal to the angle E.
Next:
Van Schooten's Ruler Constructions - Solution to Problem VIII
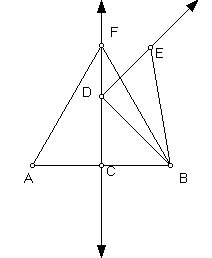
Problem VIII: Above a given straight line AB, to construct an equilateral triangle.
Construction: Cut AB by the second problem, into two equal parts at C, and from C, above AB, by the 5th problem, erect a perpendicular CF and locate on it DC equal to AC or CB. Draw DB and above that construct, as in the 5th problem, a perpendicular to DE at D, and equal to DC, and join EB. I say that if CF is made equal to BE and the triangle AF, FB is made, then the triangle AFB is equilateral.
Next:
Van Schooten's Ruler Constructions - Solution to Problem IX
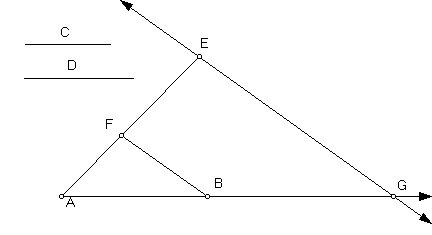
Problem IX: Given a straight line AB, to extend it to G so that the total AG to the extreme GB has a given ratio C to D.
Construction: Draw from A a line AE making any angle with AB, and put on it AF equal to C and EF equal to D. Join FB. I say that if a parallel EG is drawn to that, intersecting AB extended at G, then AG is to GB as AE is to EF, that is, C to D.
Next:
Van Schooten's Ruler Constructions - Solution to Problem X
Problem X: Given three straight lines AG, BC and AD, to find a fourth proportional DE, that is so that AB is to BC as AD is to DE.
This problem can be done in the manner of Euclid, putting the first two lines AB, BC in a straight line AC, and the third on another line AE, which forms an angle CAE with AC. If BD is drawn parallel to CE, then DE is the fourth proportional being sought.

Next:
Van Schooten's Ruler Constructions - Note to Teachers
There are a number of ways to use this material in a geometry class. Here is a plan that could be used. We give more activities than most teachers would want to use. Teachers who want to devote less time to this material may cut activities as they see fit.
I. Read the biographical and historical Introduction.
A. Briefly describe the contributions of one of the four most important mathematicians mentioned here. For this, the MacTutor History of Mathematics Archive is one useful source.
1. Vieté
2. Descartes
3. Huygens
4. Newton
B. Try an exercise with a trig table of the style van Schooten used. Here are trigonometry exercise with a table based on a radius of 200.
C. If they are very good at analytic geometry and know about focus and directrix, you might ask your students to figure out how van Schooten’s two mechanisms work to draw an ellipse or a parabola. Van Schooten's parabola drawer and ellipse drawer are shown at work in Figures 2, 6, and 8 of the module "Curve Drawing Then and Now" in the Convergence article, "Historical Activities for Calculus."
II. The first two ruler constructions (Problems I and II)
A. Go over the detailed first solution to the first problem, bisecting an angle. Note how the third postulate works.
B. Mention that circles still exist in van Schooten’s geometry. It’s just that you can’t construct them with the available tools. In much the same way, parabolas and ellipses exist in Euclid’s geometry, but you can’t construct them with a ruler and compass.
C. Ask the students to prove that the first solution actually works.
D. Ask the students to go over van Schooten’s other solutions to Problem I and his solutions to Problem II.
E. Discuss why people are interested in solving the same problem more than one way.
F. Discuss why van Schooten may have been interested in solving geometry problems without a compass.
Let your students try to solve these problems on their own. Expect them to be rather challenging. Require that they prove that their solutions are correct. Unless they can prove correctness, the solutions are probably not correct.
It is probably too much ask your students to solve all eight problems at once. You might want to use them more slowly, two or three a week for three or four weeks.
Some problems are harder than others. Problems IV and VIII are kind of tricky.
Problem V depends on solving Problems III and IV first, but then it is very easy.
Problem VI depends on solving problems IV and V first, and is fairly easy, though not as easy as Problem V.
Problem VII depends on solving Problems II and VI first. Then it is fairly easy.
Problem VIII depends on solving Problem II and V. This problem is rather difficult.
Problem IX depends on Problem III. This problem is rather easy, if you already know how to do it using Euclidean techniques.
Next:
Van Schooten's Ruler Constructions - Trigonometry Exercises
Here is a trig table based on a circle of radius 200. Angles are given in degrees. You can tell that the circle is of radius 200 because the table gives sin 90 as 200.
|
Angle |
Sin |
Tan |
Sec |
|
0 |
0 |
0 |
200 |
|
10 |
35 |
35 |
203 |
|
20 |
68 |
73 |
213 |
|
30 |
100 |
115 |
231 |
|
40 |
129 |
168 |
261 |
|
45 |
141 |
200 |
283 |
|
50 |
153 |
238 |
311 |
|
60 |
173 |
346 |
400 |
|
70 |
188 |
549 |
585 |
|
80 |
197 |
1134 |
1152 |
|
90 |
200 |
|
|
Questions
1. How does sin 90 = 200 tell you that the circle is of radius 200?
2. How can you use this table to get our modern value of sin 45, which we know to be about 0.701?
3. How can you use this table to get cosines?
4. In this table, is it still true that tan x = (sin x)/(cos x)? How about sec x = 1/cos x? Why or why not?
5. Suppose ABC is a right triangle with right angle at C, and that sides a, b, c are opposite angles A, B, C, respectively. If b = 25 and if A = 40°, then use the table to find the length of side a. You should not convert to modern values of sine and cosine. In fact, it is better if you do not use any decimals, only fractions and whole numbers.
6. Suppose that ABC is a right triangle, with A = 20° and c = 40. Find a.
Next:
Van Schooten's Ruler Constructions - Solutions to Trigonometry Exercises
1. If a segment of length r is at an angle A to a base, and the top of the segment is at distance r sin A from the base, using modern sines. We’re given that A = 90° and that the distance is 200. This makes r = 200 as well.
2. We can divide 141, the given value for sin 45, by the "total sine", 200, and get 0.705, which is correct to two decimal places. In fact, all the values in the table are 200 times their usual values.
3. It is still true that cos A = sin (90°- A). So, for example, cos 40° = sin (90°- 40°) = sin 50° = 153.
4. For this calculation, let’s use capital letters for the functions given in the table, and lower case letters for the modern functions. Then SIN x/COS x = (200 sin x)/(200 cos x) = tan x = (TAN x)/200, and this is not equal to TAN x, so the statement is not true. A student at the time would have learned to write TOT SIN for the radius of the circle involved, and then learned trigonometric identities like SIN x/COS x = TAN x/TOT SIN. That student would have learned it in ratio form, though, so the identity would have looked like SIN x : COS x :: TAN x : TOT SIN.
Similarly, 1/COS x = 1/(200 cos x) = (sec x)/200 = (SEC x)/(2002) = (SEC x)/((TOT SIN)2), and this is not equal to SEC x. Again, the proposed statement is not true.
5. You might start with a/b = TAN A/TOT SIN. This makes 168/200 = a/25, so a = 25•168/200 = 21. Modern methods give a value of 20.9775.
6. You might start with a/c = SIN A/TOT SIN. This gives a/40 = 68/200, so a = 68•40/200 = 13 3/5. Modern methods give 13.6808
Next:
Van Schooten's Ruler Constructions - Conclusions
We can only speculate why van Schooten wanted to study constructions that did not use a compass. It seems unlikely that he really mistrusted the accuracy or truth of a compass construction more than he mistrusted making marks on a ruler. So, it may be that he simply relished the intellectual challenge of using different geometric tools. Whatever his reasons, we can be grateful for these delightful nuggets of geometry from so long ago.