This article is dedicated to all those students for whom the limit is their most bitter memory of calculus. I grant that the limit really is the heart of calculus and one of the most powerful ideas in mathematics today. I also grant that the story of how the limit evolved from being a logically-suspect proving tool in the hands of analysts like Newton and Leibniz in the 17th century into a highly-polished mathematical definition articulated by Cauchy in the 19th century is one of the more interesting stories in the history of mathematics. But it turns out that many results from calculus--including the pivotal fundamental theorem of calculus--can be proved without any notion of the limit whatsoever. In fact, my aim is to present a proof of the FTC using only mathematical tools that were available to Euclid nearly 2000 years before mathematicians began wrestling seriously with the idea of the limit.

What's especially interesting about this proof is that it is not new. It's part of an often-overlooked chapter in the history of mathematics in which mathematicians endeavored to answer questions our students first see in calculus using the well-worn proving techniques of Euclidean geometry instead of the analytic techniques developed in the 17th century. Years before Newton and Leibniz published the results that eventually grew into the calculus we learn today, the proof I will present appeared in slightly modified form buried in the proof of a proposition found in The Universal Part of Geometry, a geometry book published in 1668 by the Scottish mathematician James Gregory.

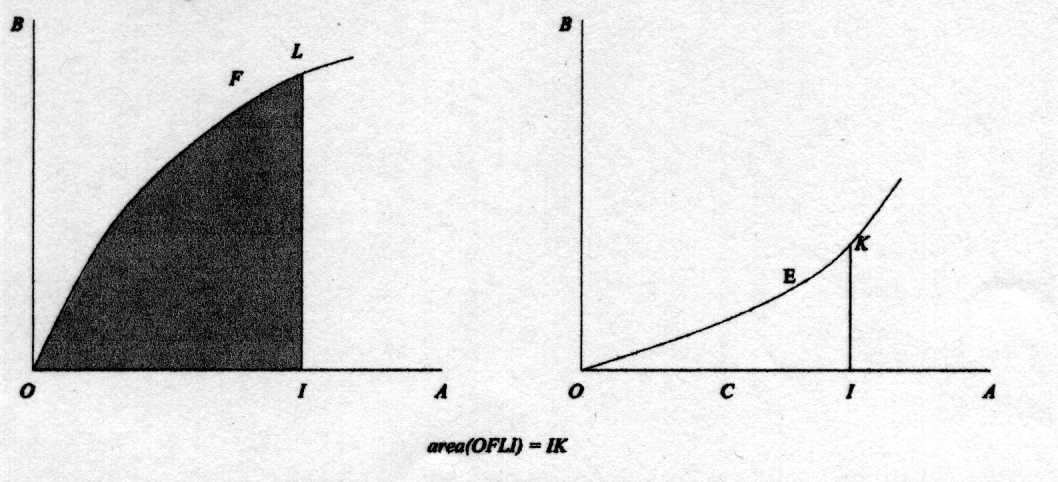
For us, the FTC is about a relation between a continuous function f(x) and its indefinite integral F(x) = ò^x_x0 f(t) dt, so it may be surprising that Gregory was able to state the result without using the language of functions. The idea behind the alternative geometric approach is simply to focus on curves like those formed by the graphs of f(x) and F(x). In particular, instead of considering a function f(x) graphed on the x- and y-axes, suppose that OA and OB are line segments perpendicular to each other at the point O and that OFL is a curve that `passes the vertical line test', so that it can be thought of as formed by the graph of a function f(x). (Following the custom of many classical Euclidean geometers, Gregory denotes an arbitrary curve by three points chosen at random on the curve. Later on, these points will each take on a specific meaning.) Next, define another curve OEK point-wise as follows: at each point I on the line segment OA the length IK of the perpendicular line segment between OA and OEK is equal to the area of the curved region OFLI.

 

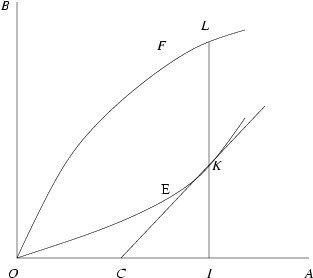
In modern terms, the curve OEK is the graph of F(x) = ò^x₀f(t) dt. The FTC states that F¢(x) = f(x) for each x in the interval. Since F¢(x) is the slope of the tangent line to F(x) at x, in geometrical terms this is equivalent to saying that for any I on the line segment OA, if C is the point where the tangent line KC to the curve OEK at K intersects OA, then the slope IK/IC of this tangent line equals IL. The proof will be established by showing that this relation holds between the points C, K, and L.

 

Gregory's proof is not without its limitations. To begin with, it assumes that the curve OFL passes through the origin and is increasing, so it is only valid for a specific case of the FTC. More importantly, at several crucial junctures Gregory relies heavily on geometrical intuition to an extent that would make most mathematicians today uneasy. The most obvious geometrical assumption is that the curve OEK as defined point-wise above actually has a tangent line at each of its points. Indeed, Gregory not only assumes this, but his figure (see below) indicates that he knew the indefinite integral of an increasing function must be concave up.

The second geometrical assumption is about the nature of a tangent line. In Gregory's proof, the crucial idea is to suppose that C is the point on the segment OA such that IK/IC = IL but that KC is not tangent to the curve OEK. The rest of the proof consists of using this claim to derive a contradiction. But what does it mean for KC not to be tangent to OEK? For someone trained in classical Euclidean geometry, the definition of a tangent line was inherited from Greek mathematicians such as Euclid (in the Elements III.16) and Apollonius (in the Conics I.33, et al ). For these geometers, a line is tangent to a curve when (i) the line touches the curve at one point and (ii) all other points on the line lie on one side of the curve.

 

This definition is slightly different from the definition we use today and has the drawback of only working for curves where the concavity doesn't change sign. For instance, the tangent line to f(x) = x³ at x = 0 wouldn't satisfy this definition. But it has the benefit that a line will not be tangent to a curve precisely when the part of the line on one side of its intersection with the curve is above the curve, while the other part is below.

This Euclidean definition of the tangent is pivotal to Gregory's contradiction. For if KC is not tangent to OEK, it means that some point a on KC must lie above the curve OEK. In particular, if DF is the line segment perpendicular to OA which intersects OA at D, OEK at E, KC at a, and OFL at F, then DE < Da by choice of a. This is shown in the figure below (adapted from Gregory's proof-see the Appendix ).

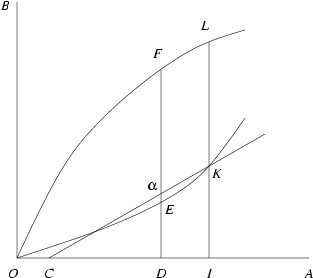
Actually, the figure tells only half of the story. It's also possible that a could lie on the other side of K on the line CK. However, the argument for that case is similar, and the details make a good exercise (or see the Appendix ).

By the definition of the curve OEK, if area(OFD) denotes the area enclosed by the curve OF and the line segments OD and DF, then DE = area(OFD). Likewise, IK = area(OFLI). Thus, IK/DE = area(OFLI)/area(OFD). Since DE < Da, it follows that IK/Da < IK/DE and so

IK Da < area(OFLI) area(OFD) .

Notice that C, a, and K are collinear and that IK and Da are both perpendicular to OA. Thus, the triangles CDa and CIK are similar. So by corresponding sides, IK/Da = IC/DC and hence IC/DC < area(OFLI)/area(OFD). Now multiply the numerator and denominator in IC/DC by IL to obtain IC/DC = IC·IL/ DC·IL. It follows that

IC·IL DC·IL < area(OFLI) area(OFD)

This last step may seem mysterious, but it serves the purpose of converting the original inequality into an inequality about areas which will lead Gregory to an obvious geometrical contradiction. Specifically, DC·IL is the area of the rectangle with sides IL and DC, and IL·IC is the area of the rectangle with sides IL and IC. Inverting the ratios in the last inequality yields:

area(OFD) area(OFLI) < DC·IL IC·IL

Now we can make some observations about these areas to arrive at a contradiction: Note that area(OFLI) = area(OFD) + area(DFLI) and likewise, since IC = DI + DC, IC·IL = DI·IL + DC ·IL. Substituting these expressions into the numerators of the last inequality and doing some algebra, we have

area(OFLI) - area(DFLI) area(OFLI) < IC ·IL - DI·IL IC·IL Û 1 - area(DFLI) area(OFLI) < 1 - DI·IL IC·IL Û DI ·IL IC·IL < area(DFLI) area(OFLI) .

But recall the defining equality for C-namely, IK/IC = IL. This implies that IK = IC·IL. Since IK = area(OFLI) by definition of the curve OEK, the denominators in the last inequality are the same. Therefore, the numerators must satisfy DI·IL < area(DFLI). But remember that OFL is increasing by assumption. Thus, the rectangle with sides IL and DI must circumscribe the region DFLI.

 

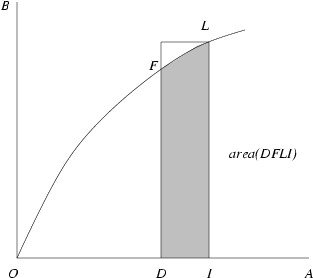
Hence area(DFLI) < DI ·IL as well. This contradiction shows that KC must in fact be tangent to OEK. Hence the fundamental theorem of calculus follows.

So why hasn't Gregory received the same sort of accolades usually given to Newton and Leibniz? Probably the most persuasive argument against Gregory's role in the discovery of the FTC is that he didn't realize what he had. For Gregory, the FTC is essentially a technical lemma which is used without comment in the course of proving a result which most today would find uninteresting. It isn't even stated explicitly. However, instead of arguing this point, I'll let you decide for yourself. Follow this link  for a translation of the proposition where the FTC occurs and this link  for the Latin original.

Also, as noted above, Gregory's proof of the FTC is not without its problems, so some may point to a lack of rigor. But given the standards of rigor of the day, Gregory's omissions in the proof were probably not considered serious. In Gregory's time Euclid was the model of mathematical rigor, although he makes the same sorts of oversights even in the first proof he presents in the Elements . Because it makes use of these Euclidean techniques, the geometrical work of Gregory was undoubtedly considered very rigorous, especially when compared to the proofs offered by Newton and the other analysts. It would be 150 years before the analytic methods they used were given the rigorous "d-e" foundation known today.

On the other hand, it's likely that one reason Gregory's work is largely forgotten is precisely because he avoided the limit. Euclidean geometry is a mathematics for describing static relations between unchanging objects. But calculus today is often called "the language of change". Newton, Leibniz, and the other analysts are celebrated for introducing an entirely new and much more powerful way of looking at the same problems. It was this way of thinking later codified in the limit we learn today that was paramount, because it gave mathematics a new-found power to model the constantly changing world we live in.

But this also points to a reason why Gregory's work should be interesting for educators. For many students, Euclidean geometry is simply a stepping stone to the vastly more powerful tools of analytic geometry, useful only for studying simple relations between points, lines, and circles. But the work of Gregory shows just how rich the elementary language of geometrical similarity really is. Indeed, Gregory's geometrical arguments are interesting precisely because they push the language of Euclidean geometry further than most would have believed possible.

Gregory wasn't alone in using Euclidean methods to prove theorems in calculus. In 1670, Cambridge mathematician Isaac Barrow published the Lectiones Geometricae , which also proved many results from Calculus-including the FTC-using only geometry. This work is presented in a highly-annotated (and somewhat controversial) book entitled The Geometrical Lectures of Isaac Barrow published in 1916 by J.M. Child (Open Court Publishing Company).

For a general introduction to the work of Gregory and Barrow (along with the work of many other contributors to the foundations of calculus), see The Origins of the Infinitesimal Calculus by Margaret E. Baron, available (cheaply!) from Dover Publications. Victor Katz also has a good discussion of Barrow's geometrical proof of the FTC in his book A History of Mathematics: An Introduction (2nd edition) (Addison-Wesley). (See pages 500-501.)

Gregory's proof of the FTC is found in the proof of Proposition Six of the Universal Part of Geometry . In modern terms, if f(y) is a function (with graph BHNS in the figure below), the goal of this proposition is to construct a function g(y), whose arc length has the same ratio to its axis as the area under the graph of f(y) has to an inscribed rectangle with the same base. In other words, given f(y), the goal is to find a function g(y) such that

arclength(g(y)) y = ó õ y 0  f(t) dt c y

where y is arbitrary and c is the length of the segment AB, or

ó õ y 0  Ö   1 + (g¢(t))2    dt = 1 c ó õ y 0  f(t) dt

The FTC appears in the construction of the function g(y). First, he constructs a function h(y) via the defining equation f(y)² = c² +h(y)². (In terms of the figure, AI = y, IM = BA = c, and h(y) is the curve AFLP.) Then g(y), which has graph AKQ, is defined by c g(y) = ò^y₀ h(t) dt. The bulk of the proof is then devoted to showing that if c g(y) = ò^y₀h(t) dt, then c g¢(y) = h(y), and this is precisely the FTC.

Proposition 6. Problem.

To find a curve which has the same ratio to its axis as any exhibited figure has to a rectangle inscribed in it and applied to a given line or axis of the sought-after curve.

Let the exhibited figure be ABSO and let the inscribed rectangle be ABRO. Let the curve BS be simple or non-winding, but if it is not, the curve ought to be divided into many simple parts and the demonstration carried out separately. Next, let the curve AFLP be of such a nature that when any line IN is drawn normal to the line AO and cutting the curve AFLP in L, the square on IN will equal a sum of the squares of both IL and IM. Next, let the curve AEKQ be drawn of such a nature that when any line IM is drawn perpendicular to the line AO and cutting the curve AEKQ in K and AFLP in L, the rectangle MIK is equal to the curved region IAFL. I say that the figure ABSO is to the rectangle ABRO as the curve AEKQ is to the line AO.

 

For let K be a point on the curve AEKQ, through which is drawn the line IN perpendicular to the line AO and cutting the curves AFLP, BR, and BHNS in the points L, M, and N. Let IK be to IC as IL is to IM and let KC be drawn. The line KC either cuts or is tangent to the curve AQ in the point K. If possible, let it cut the curve at K and let it will fall within the curve at a point E toward the vertex A. Through the point E let a line DH be drawn parallel to IN and cutting AQ, AP, BR, and BS in the points E, F, G, and H, and the line KC in a. Also, complete the rectangle ILZC, whose side LZ cuts the line DH at X. Since IL is to IM as IK is to IC, the rectangle MIK-or the curved region IAFL-will be equal to the rectangle IZ. Since the rectangle GDE is equal to the curved region DAF, as IK is to DE thus will the curved region IAFL be to the curved region DAF. But IK has a greater ratio to DE than to Da. Thus, the curved region IAFL has a greater ratio to the curved region DAF than IK has to Da-or IC has to DC. Therefore, the curved region IAFL has a greater ratio to the curved region DAF than the rectangle IZ has to the rectangle DZ, and, per conversionem rationis , the curved region IAFL has a smaller ratio to the curved region IDFL than the rectangle IZ has to the rectangle IX. By permuting, the curved region IAFL has a smaller ratio to the rectangle IZ than the curved region IDFL has to the rectangle IX. Since the rectangle IZ is equal to the curved region IAFL, the rectangle IX will be less than the curved region IDFL. But it is also more than the curved region IDFL, which is absurd. Consequently, the line KC does not fall within the curve AQ toward the vertex.

If possible, let the line CK fall within the curve toward the base, with the remaining things holding as in the previous situation. As IK is to DE, thus will the curved region IAFL be to the curved region DALF. But IK has a greater ratio to DE than to Da. Therefore, the curved region IAFL has a greater ratio to the curved region DALF than IK has to Da-or IC has to DC. Therefore, the curved region IAFL has a greater ratio to the curved region DALF than the rectangle IZ has to the rectangle DZ. Through inverting, conversionem rationis , and inverting in turn, the curved region IAFL has a greater ratio to the curved region IDFL than the rectangle IZ has to the rectangle IX. By permuting, the curved region IAFL has a greater ratio the rectangle IZ than the curved region IDFL has to the rectangle IX. Since the curved region IAFL is equal to the rectangle IZ, the rectangle IX will be more than the curved region IDFL. But it is also less, which is absurd. Therefore, the line CK does not fall within the curve AQ toward the base. Thus, the line KC is tangent to the curve AQ in the point K.

Let the line KT, intersecting the line AO in T, be perpendicular to the line CK. It is manifest that CI is to CK as IK is to KT. But CI is to CK as MI is to NI, since the lines IN, IM, and IL are a right triangle similar to the triangle CIK, with sides IM and IN corresponding to the sides CI and CK. Consequently, as IK is to KT, thus is IM to IN. Since it is done in the same manner for all points of the curve AQ, it is manifest from Proposition Two that the line AO is to the curve AQ as the rectangle OB is to the figure ABSO, which it was desired to demonstrate.

Propositio 6. Problema.

Invenire curvam, quae ad suum axem eandem habeat rationem, quam figure qualibet exhibita ad rectangulum sibi inscriptum, et rectae datae seu quaesitae curvae axi applicatum.

Sit figure exhibita ABSO, rectangulum inscriptum ABRO; sitque curva BS simplex seu non sinuosa, si autem sit, dividenda est in plures simplices, et demonstratio seorsim instituenda. Deinde sit curva AFLP talis naturae, ut, ducta recta quacunque IN normali rectae AO, curvam AFLP secante in L, recta IN sit aequalis potentia utrique IL, IM; deinde ducatur curva AEKQ talis naturae, ut, ducta recta quacunque IM rectae AO perpendiculari et curvam AEKQ secante in K et AFLP in L, rectangulum MIL sit aequale mixtilineo IAFL. Dico figuram ABSO esse ad rectangulum ABRO ut curva AEKQ ad rectam AO. Sit in curva AFLP punctum ad libitum K, per quod ducatur recta IN, perpendicularis rectae AO et lineas AFLP, BR, BHNS, secans in L, M, N, punctis; sitque ut IL ad IM ita IK ad IC et ducatur KC: recta KC curvam AQ secat vel tangit in puncto K; si fieri potest, cam secet in K, et ideo intra curvam cadet nempe intra punctum E versus verticem A: ducatur per punctum E recta DH rectae IN parallella lineas AQ, AP, BR, BS, secans in punctis E, F, G, H, et rectam LC in a, item compleatur rectangulum ILZC, cuius latus LZ rectam DH secet in X. Quoniam IL est ad IM ut IK ad IC, erit rectangulum MIK seu mixtilineum IAFL aequale rectangulo IZ; et quonium rectangulum GDE est aequale mixtilineo DAF, erit ut IK ad DE ita mixtilineum IAFL ad mixtilineum DAF, at IK ad DE maiorem habet rationem quam ad Da; et ideo mixtilineum IAFL maiorem habet rationem ad mixtilineum DAF quam IK habet ad Da seu IC ad DC; et igitur mixtilineum IAFL maiorem habet rationem ad mixtilineum DAF quam rectagulum IZ ad rectangulum DZ, et per conversionem rationis mixtilineum IAFL ad mixtilineum IDFL habet minorem rationem quam rectangulum IZ ad rectangulum IX, et permutando mixtilineum IAFL ad rectagulum IZ minorem habet rationem quam mixtilineum IDFL ad rectangulum IX, cumque rectangulum IZ sit aequale mixtilineo IAFL, erit rectangulum IX minus mixtilineo IDFL, sed et maius est, quod est absurdum; et proinde recta KC intra curvam AQ non cadit versus verticem: si fieri potest, cadat recta CK intra curvam versus basem reliquis se habentibus ut in priore positione; eritque ut IK ad DE ita mixtilineum IAFL ad mixtilineum DALF, at IK ad DE maiorem habet rationem quam ad Da,; et ideo mixtilineum IAFL ad mixtilineum DALF, maiorem habet rationem quam IK ad Da seu IC ad DC; et igitur mixtilineum IAFL ad mixtilineum DALF maiorem habet rationem quam rectangulum IZ ad rectangulum DZ, et invertendo, per conversionem rationis et rursus invertendo, mixtilineum IAFL ad mixtilineum IDFL maiorem habet rationem quam rectangulum IZ ad rectangulum IX, et permutando mixtilineum IAFL ad rectangulum IZ maiorem habet rationem quam mixtilineum IDFL ad rectangulum IX, cumque mixtilineum IAFL sit aequale rectangulo IZ, erit rectangulum IX maius quam mixtilineum IDFL, sed et minus est, quod est absurdum; non cadit ergo recta CK intra curvam AQ versus basem; et ideo recta KC curvam AQ tangit in puncto K, rectae CK sit perpendicularis recta KT rectae AO occurrens in T; manifestum est CI esse ad CK ut IK ad KT; atque CI est ad CK ut MI ad NI, quoniam rectae IN, IM, IL efficiunt triangulum rectangulum simile triangulo CIK, cuius latera IM, IN, sunt homologa lateribus CI, CK et proinde ut IK ad KT ita IM ad IN; cumque hoc eodem modo fiat in omnibus punctis curvae AQ, manifestum est ex huius 2 rectam AO esse ad curvam AQ ut rectangulum OB ad figuram ABSO, quod demonstrare oportuit.