Teaching Leonardo: An Integrated Approach
Editors’ Note: The history of mathematics readily lends itself to interdisciplinary teaching. Rick Faloon, a mathematics instructor at the Ross School, East Hampton, NY, joined with colleagues in other disciplines to develop a student project involving aspects of the Renaissance. During an NCTM Annual Meeting in Philadelphia, Rick gave a poster presentation on his project and its results. The pages that follow contain an outline of the project, together with some students’ work. For more information on this exciting strategy of using the history of mathematics in teaching, contact Rick Faloon directly at rfaloon@ross.org.

The ninth grade integrated Leonardo notebook project was co-designed by high school art, mathematics, and science faculty. Taught in conjunction with a cultural history unit on the Renaissance, the aim of this project was to encourage students to think expansively across disciplines and perform like a Renaissance person by producing notes, drawings, and mathematical calculations based on their own observations and experiences. As the notebooks demonstrate, students used Renaissance drawing methods, such as crosshatching, foreshortening, and perspective, to create botanical drawings, drawings of inventions and mechanical objects, master copies, studies from the model, and other observational drawings. The science component involved dissecting animals and producing drawings that rendered and identified organs. In mathematics, students measured and drew geometric forms and calculated their volumes. They learned Geometer's Sketchpad and used it to analyze the perspective used in Renaissance paintings as well as to digitally produce their own perspective drawings. In addition, they made measurements of the proportions of the Vitruvian Man (above) and were able to determine their correspondence to the Golden Mean and the Fibonacci Sequence.
Teaching Leonardo: An Integrated Approach - Introduction
Editors’ Note: The history of mathematics readily lends itself to interdisciplinary teaching. Rick Faloon, a mathematics instructor at the Ross School, East Hampton, NY, joined with colleagues in other disciplines to develop a student project involving aspects of the Renaissance. During an NCTM Annual Meeting in Philadelphia, Rick gave a poster presentation on his project and its results. The pages that follow contain an outline of the project, together with some students’ work. For more information on this exciting strategy of using the history of mathematics in teaching, contact Rick Faloon directly at rfaloon@ross.org.

The ninth grade integrated Leonardo notebook project was co-designed by high school art, mathematics, and science faculty. Taught in conjunction with a cultural history unit on the Renaissance, the aim of this project was to encourage students to think expansively across disciplines and perform like a Renaissance person by producing notes, drawings, and mathematical calculations based on their own observations and experiences. As the notebooks demonstrate, students used Renaissance drawing methods, such as crosshatching, foreshortening, and perspective, to create botanical drawings, drawings of inventions and mechanical objects, master copies, studies from the model, and other observational drawings. The science component involved dissecting animals and producing drawings that rendered and identified organs. In mathematics, students measured and drew geometric forms and calculated their volumes. They learned Geometer's Sketchpad and used it to analyze the perspective used in Renaissance paintings as well as to digitally produce their own perspective drawings. In addition, they made measurements of the proportions of the Vitruvian Man (above) and were able to determine their correspondence to the Golden Mean and the Fibonacci Sequence.
Teaching Leonardo: An Integrated Approach - Renaissance Notebook Assignment
Over the course of this trimester each of you will create pages for a Renaissance notebook inspired by the work of Leonardo Da Vinci and by other Renaissance artists. The objective of this project is to give you an opportunity to perform like a Renaissance person by making your own observational sketches, perspective studies, mathematical calculations, scientific notes and drawings.
Your notebook must contain competent examples of the following:
Art
- Imagined creature drawing blind contour drawing (palm of hand)
- Modified contour drawing (hand)
- Mechanical drawing (from boat or from mechanical objects in class)
- Leaf drawing (using contour in ink and pencil)
- Tonal drawing of torso (using chiaroscuro sfumato)
- Silverpoint drawing
- 10 quotations from Leonardo
- 10 quotes from others including the Vasari quotation (relating to Leonardo’s seven traits)
- Leonardo biography page
- List of seven traits of Leonardo with your commentary on your own traits
- Anatomy drawing from model (with muscles labeled)
- Gesture drawings of figure (using ink, conte, etc)
- Facial expression drawing
- Backwards writing
- Art history images/pages with notes
- Master copies
- Michelangelo back drawing (crosshatching)
- Mantegna - Dead Christ (foreshortening)
- 3 copies of works of Leonardo or other Renaissance artists
Mathematics
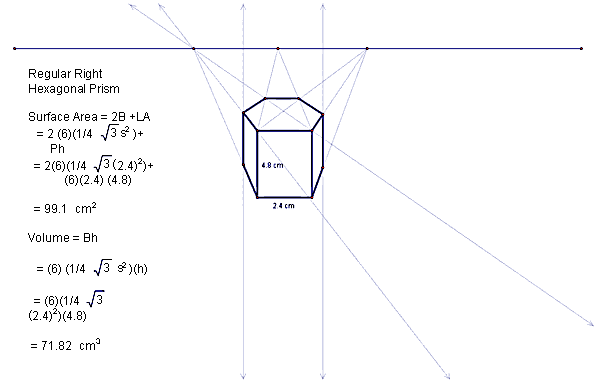
- 2 drawings of Platonic Solids using 1 or 2 point perspective. Show area and volume.
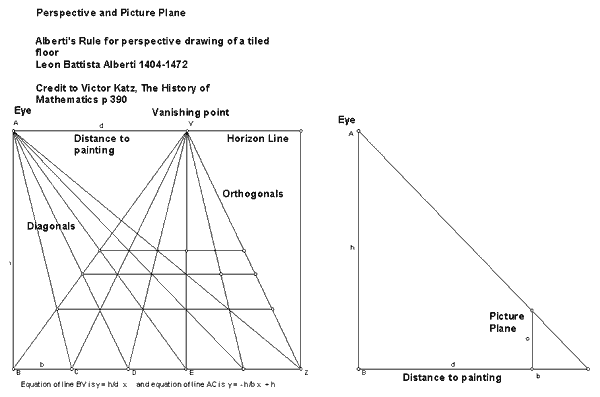
- Tiled Piazza in 1 point linear perspective. Show all measurements and correct perspective. Include quotation by Pierro della Francesca.
- Vitruvian Man and Golden Mean
- Fibonacci Sequence
- Mathematical evaluation of a Renaissance Painting showing horizon line, vanishing point, orthogonal lines, eye point, and correct ratios demonstrating correct linear perspective.
Science
- 2 Dissection drawings (done in science class in conjunction with dissection)
- Drawing of simple machine in Leonardo style; explanation of physics of mechanism
On the following pages are examples of students' work from the mathematics section of the project.
Teaching Leonardo: An Integrated Approach - Tiling a Floor Using Geometer's Sketchpad

INSTRUCTIONS FOR PERSPECTIVE DRAWING OF
TILE FLOOR USING GEOMETER’S SKETCHPAD
1. Place and label point A near bottom of screen.
2. Place and label point C along horizontal line also near bottom of screen, several inches away from A.
3. Construct line segment AC.
4. Construct midpoint of segment AC.
5. Label the midpoint B.
6. Construct the midpoint of segment AB and label it D. To do this you will have to select points A and B and construct the segment AB. This will appear on top of the segment already constructed. Then you can select that segment and construct its midpoint.
7. Construct the midpoint of segment BC (as in step 6) and label it E.
8. Place and label point Z several inches above AC and approximately over the point B.
9. Construct segments AZ, BZ, CZ, DZ, and EZ.
10. Construct a line through Z parallel to AC.
11. On new line constructed in step 10 above construct and label point X to the left and several inches away.
12. Construct DX.
13. Construct the point of intersection of AZ and DX and label the point L .
14. Construct BX.
15. Construct the point of intersection of AZ and BX and label the point M.
16. Construct EX.
17. Construct the point of intersection of AZ and EX and label the point N .
18. Construct ray through L and parallel to AC. Note that this line goes through the intersection point of DZ and BX. Construct that intersection point and label it P .
19. Construct ray through M parallel to AC. Note that this line goes through the intersection point of EX and DZ. Construct that intersection point and label it Q .
20. Construct ray through N and parallel to AC .
21. (Optional: You may “clean up” the drawing or skip this step.) Select and undo the construction lines DL, MB and EN. Color in “tiles” to make drawing appear more like a tile floor, by constructing the polygon interior and selecting a color from the display menu.
22. Optional: You may want to construct columns at the edge of your tile floor. To do this, construct a line segment at A perpendicular to AC. Make this line segment a bit longer than AD. Label the upper endpoint of this line segment S and construct SZ. Then construct line segments from L, M, N each perpendicular to AC and ending on the line segment SZ. These constructions will take some thought, because you will probably have to construct certain lines and later delete certain parts of the line. Think carefully about how to do this.
23. a) Label the vanishing point.
b) Label the horizon line.
c) Measure the length XZ. This is the viewing distance of the painting.
d) Measure the line segments to find the ratios of PL to AD and of
XZ to (XZ+AD)
24. The Renaissance artist/mathematian Piero della Francesca (1420-1492) said that “the ratio of the first line to the second line is always proportional to the ratio of the distances from the eye to the first line and from the second to the eye.” Copy and paste this quotation onto your drawing and measure the following lengths to show that these ratios are the same: MQ to AD; XZ to (XZ+2AD).
25. If you have constructed the columns in step 22, find the ratio of the length of the second column to the first (AS). Show that this ratio is the same as that of PL to AD. Similarly, find the ratio of the length of the third column to the first and show that it is the same as that of MQ to AD.
Teaching Leonardo: An Integrated Approach - More on Perspective
A. Connect to the website Exploring Leonardo: http://www.mos.org/sln/Leonardo/
Follow the links to Leonardo's Perspective and Exploring Linear Perspective. Read the material and do some of the activities suggested.
B. Select at least three of the paintings in the sketchpad examples. In each one, sketch appropriate lines to find the horizon line and vanishing point Z for each painting. Next, find the intersection point X of several of the diagonals going in the same direction. It should be on the horizon line. Measure the distance from X to Z. This is the appropriate distance from the eye to view the painting. If possible, measure and label corresponding sides of similar triangles to show the correct proportions.
Questions:
a) Does the exactness of the perspective differ from painting to painting?
b) Which painting has the most mathematically exact perspective?
c) Which has the least?
On the following pages are examples of part B from three students.
Teaching Leonardo: An Integrated Approach - Questions for Students
Questions about Leonardo Da Vinci, the Golden Ratio, and Vitruvian Man
1
_______________|___________
x 1–x
The Golden Mean is the mean proportional between 1 and 1 – x. That is, we find the Golden Mean by solving the proportion 1:x = x:1-x for x.
1) Why is the Golden Ratio called the Divine Ratio?
2) Give two examples in ancient history where they used the Golden Ratio.
3) What is the approximate value of the Golden Ratio to the 5th decimal place?
4) What is the relation of the Golden Ratio to Fibonacci Numbers?
5) Leonardo worked with Fra Luca Paccioli to write the dissertation entitled Divina Proportione (The Divine Proportion). What are the 5 properties they said make this ratio divine?
6) On the reproduction of Leonardo’s Vitruvian Man, which was an illustration for the above dissertation, measure the ratio of the following, where E is the distance from the chin to the navel and D is the distance from the top of the head to the chin:
D/E =
E/B =
B/C =
C/A =

7) In Leonardo’s attempt at the Quadrature of the Circle, what is important about the center of the circle being the navel?
8) Find another web site dealing with Leonardo’s Vitruvian man, and write some other interesting facts about this drawing. In particular, determine other proportions in the drawing which seem to give the Golden Mean.
9) Measure a rectangle to see if the proportions fit closely to the Golden Mean (computer screen, credit card, window, white board, book, painting, calc screen, other…).
Questions about Leonardo Da Vinci and the Golden Mean
1) Reproduce the Golden Spiral using multiple Golden Rectangles in your Leonardo Notebook. (Remember that a square is added in counter clockwise fashion to the long edge of the previous rectangle.)
2) Number the length of each new long edge as the spiral grows as shown below.
3) List these numbers under the heading Fibonacci Numbers and calculate the ratio of the larger to the smaller consecutively as shown. Continue the pattern of numbers until you get to 1.618…..
Teaching Leonardo: An Integrated Approach - Student Answers
Student responses to some of the above questions:

Teaching Leonardo: An Integrated Approach - Bibliography
The following bibliography is for both students and teachers.
Books:
Byrd, Robert. Leonardo, Beautiful Dreamer. New York: Dutton Children's Books, 2003
Cianchi, Marco. Leonardo: the Anatomy. Florence: Giutni, 1984
Corsi, Jerome R. Leonardo da Vinci: A Three-Dimensional Study. Rohnert Park, CA: Pomegranate Artbooks, 1995.
Fairbrother, Trevor and Chiyo Ishikawa. Leonardo Lives: The Codex Leicester and Leonardo da Vinci’s Legacy of Art and Science. Seattle: University of Washington Press, 1997.
Farago, Claire. Leonardo da Vinci Codex Leicester: A Masterpiece of Science. New York: American Museum of Natural History, 1996.
Gelb, Michael J. How To Think Like Leonardo: Seven Steps to Genius Everyday. New York:Delacourt Press, 1998.
Hebert, Janis. Leonardo da Vinci for Kids: His Life and Ideas. Chicago: Chicago Review Press, 1998.
Maranir, Pietro. Leonardo da Vinci: The Complete Paintings. New York: Abrams. 1999.
Mason, Antony. Famous Artists: Leonardo da Vinci. London: Aladin Books, 1993.
Wallace, Robert. The World of Leonardo, 1452-1519. New York: Time, Inc., 1966.
Video:
A&E Biography, “Leonardo da Vinci: Renaissance Master,” 1997.
Websites:
Museum of Science, Boston:
http://www.mos.org/sln/Leonardo/
Metropolitan Museum:
http://www.metmuseum.org/special/Leonardo_Master_Draftsman/draftsman_splash.htm
American Museum of Natural History Codex Leicester exhibit:
http://www.amnh.org/exhibitions/codex/
Seattle Art Museum and Codex Leicester exhibit
http://seattlepi.nwsource.com/leonardo/