Completing the Square - Quadratics Using Subtraction
Another form of the quadratic equation has a negative second term; the area of a rectangle is subtracted from the area of a square. The geometric solution is a little more complex in that the two parts of the rectangle are taken from the square. The first removal requires the addition of a small square before the second half can be removed, as shown below. Consequently, the original geometric square is finally reduced in size to a smaller square.
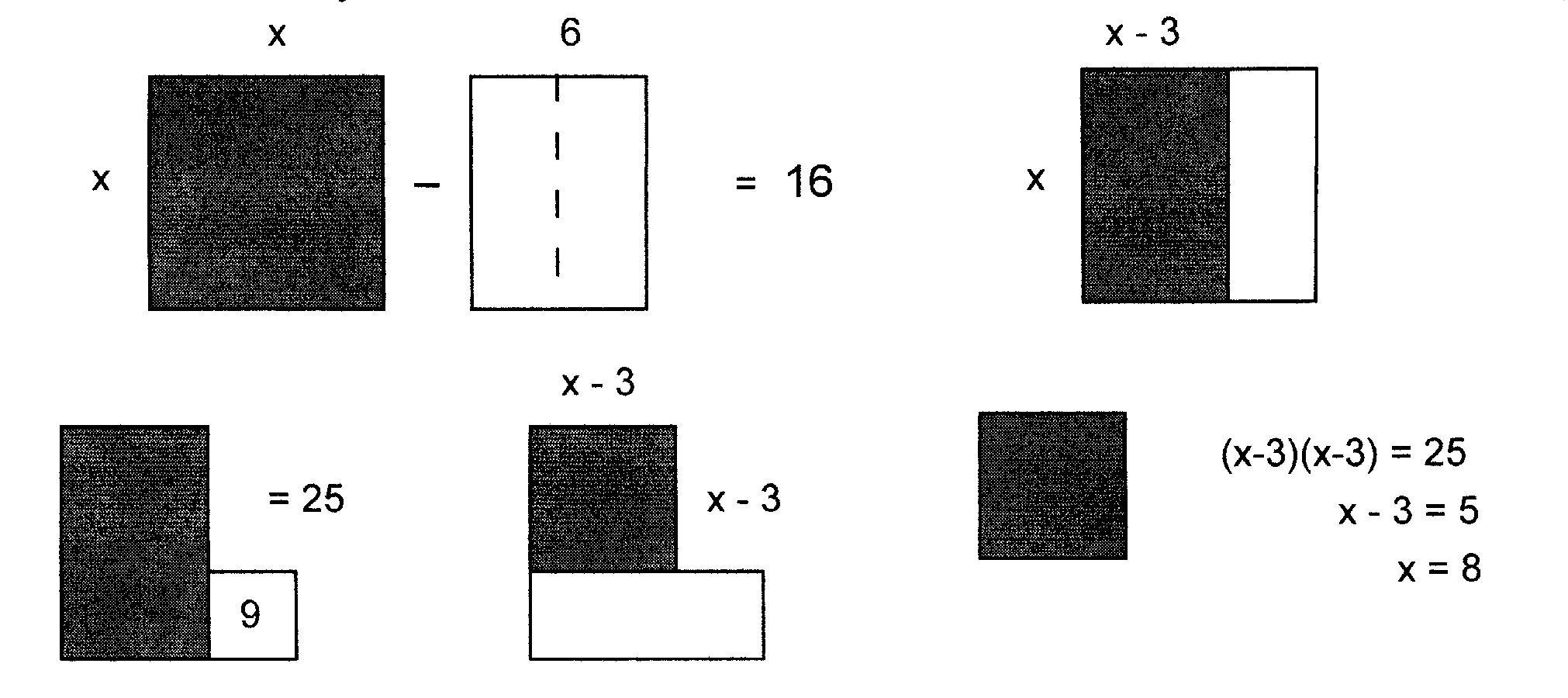
For the quadratic equation \( x^2 - 6x = 16 :\) In the upper left section of the illustration below, the terms of the equation, \( x^2 \) and \( 6x ,\) are represented by geometric figures, a square and a rectangle. The difference of their areas is given to be \( 16 .\) The rectangle is divided into two parts, each of area \( 3x .\) In the upper right section of the illustration, one of these parts is removed from the square of area \(x^2 ,\) leaving a rectangle of area \( (x-3)x .\) The goal now is to remove from this rectangle the remaining rectangle of area \( 3x.\) In the lower left section of the illustration, a \( 3\times 3\) square is attached to the rectangle, resulting in an L-shaped region that is \( 9\) units larger than the rectangle. Now a rectangle of area \( 3x\) may be removed from the L-shaped region, leaving, on the one hand, a square of area \( (x-3)(x-3) ,\) and, on the other hand, a region of area \( 16 + 9 = 25 .\) The solution to \( x^2 - 6x = 16 \) now follows easily.
Exercises: (1) \( x^2 - 10x = 24 ;\) (2) \( x^2 - 8x = 20 ;\) (3) \( x^2 - 4x = 12 .\)
In his instructions for solving quadratic equations, al-Khwarizmi wrote that if the coefficient of the squared term is not unity, then make it so by using the multiplicative inverse. (These were not his words, just his thought and instructions in modern language.) Hence, he provided for the case \( ax^2 + bx = c .\) Finally, he never envisioned an equation set equal to zero or to a negative number. An equation had to equal something positive. Consequently, the geometric method will not solve \( x^2 + 8x + 65 = 0 .\) This requires the algebraic method that was derived from al-Khwarizmi’s geometric method.