Thomas Simpson and Maxima and Minima - Ship and boat
Suppose a ship to sail from a given place A, in a given direction AQ, at the same time that a boat, from another given place B, sets out in order (if possible) to come up with her, and supposing the rate at which each vessel runs to be given; it is required to find in what direction the latter must proceed, so that if it cannot come up with the former, it may, however, approach it as near as possible (problem XV, page 32).
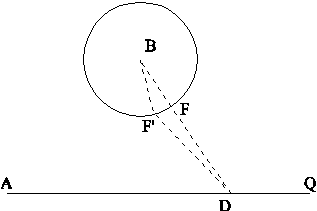
Let \(m\) be the constant velocity of the ship and \(n\) the constant velocity of the boat. If \(n \ge m\), the boat will eventually meet the ship, so we may assume that \(m > n\). After a certain time \(t\), the ship is at \(D\) while the cotemporary point for the boat is at \(F\). It is to be noted that all points on the circumference centered at \(B\) and radius \(BF\) are cotemporary with \(F\), but the boat should follow the path \(\overline{BFD}\) since any other path \(\overline{BF'D}\), with \(F'\) on the circumference, is longer.
We need to minimize \(DF\). Let \(\overline{BC}\) be the perpendicular to \(\overline{AQ}\). Define \(AC = a, BC = b, CD = x\), and \(DF = d\). Since \(D\) and \(F\) are cotemporary and time = distance/velocity we can conclude that \(\frac{AD}{m} = \frac{BF}{n}\).
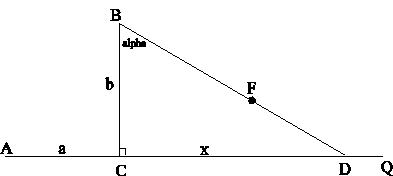
Thus \(BF = \frac{n}{m}(a + x)\), and consequently
Therefore
\(d'(x) = \frac{x}{\sqrt{b^2 + x^2}} - \frac{n}{m}\).
Making \(d'(x) = 0\), we get \(x = \frac{nb}{\sqrt{m^2 - n^2}}\), the value at which \(d(x)\) attains its minimum.
Remarks: We note that
\(\alpha = \arctan \frac{n}{\sqrt{m^2 - n^2}}\)
while
\(d(\frac{nb}{\sqrt{m^2 - n^2}}) = \frac{b\sqrt{m^2 - n^2} - na}{m}\).
So, the problem can be solved provided \(b\sqrt{m^2 - n^2} - na \ge 0\). What happens if \(b\sqrt{m^2 - n^2} - na = 0\)? This equality implies \(DF = 0\). In other words, the boat meets the ship if it takes the direction determined by the angle
\(\alpha = \arctan \frac{n}{\sqrt{m^2 - n^2}}\)
and \(b\sqrt{m^2 - n^2} - na = 0\). Whenever \(b\sqrt{m^2 - n^2} - na > 0\), we can be certain that
\(\frac{b\sqrt{m^2 - n^2} - na}{m}\)
is the minimum distance that can be achieved.
Editor’s Note: This article was published in 2005.