The Rule of False Position and Geometric Problems - First Problem
Problem: Build an equilateral triangle knowing the length of a line segment PQ equal to the side of the triangle less its height plus a third of its height.
Construction: Let BCD be any equilateral triangle. Draw the height BE and segment FG that joins the center of the triangle with the midpoint of the side BC. On the side CD take the point H so that CH = BE. On the extension of CD take the point I so that DI = FG.
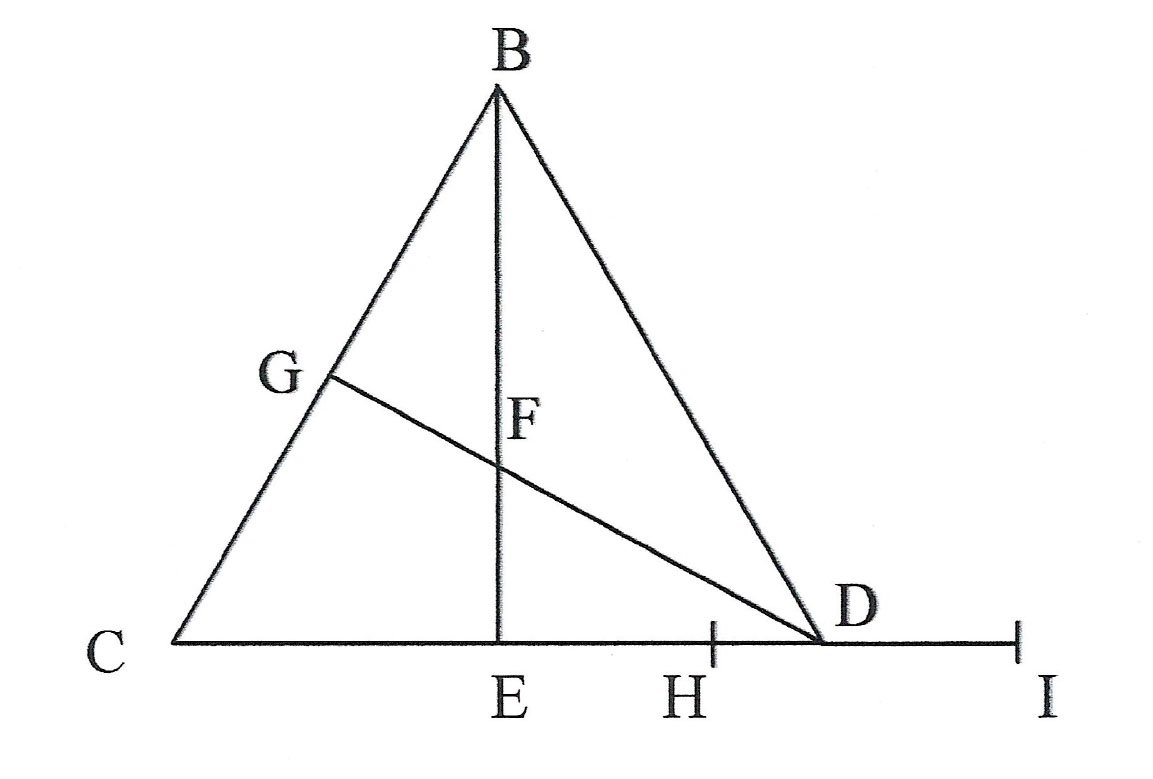
If triangle BCD is the solution to the problem, then HI will be equal to the line segment PQ. If not, the side of the equilateral triangle solution (say x) will be the fourth proportional with respect to the segments HI, PQ and BC. In other words,
HI:PQ = BC:x.