Dear Professor Greitzer - The First Identity
Calculus teachers, and their students, know that the relationship
$${{\pi}\over{4}}=\arctan{\frac{1}{2}}+\arctan{\frac{1}{3}}$$
is historically famous, as well as a quickly converging way to calculate the digits of \(\pi\), by using the Taylor series for the arctangent function:
$$\arctan x = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \frac{x^9}{9} - \cdots ,$$
but our Geometry classes know only that the two angles that go with slopes of 1/2 and 1/3 have a sum of 45 degrees. That’s OK ... we’re just glad they’re looking for patterns. Here is another one they noticed.
Hey, it looks like the angles that go with slopes of 1/5 and 1/8 (11.3o and 7.1o) have a sum of 18.4 degrees, the angle that goes with the slope of 1/3.
Slightly varying Figure 2 into Figure 3 gives us assurance that this relationship is also true.
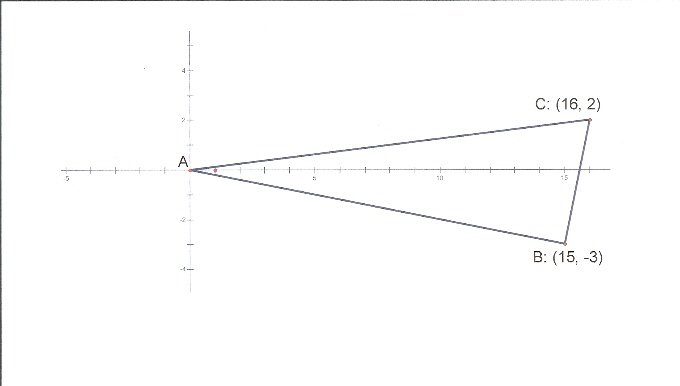
This triangle is also clearly a right triangle, since the slopes of the legs are -1/5 and 5. The short leg is 1/3 the length of the long leg, since we drew three 5 x 1 segments, and then turned 90 degrees and drew only one 5 x 1 segment. The angle at the origin must, therefore, be the one associated with a slope of 1/3, and it has also been split into two angles by the x-axis. The segment below, connecting A(0,0) and B(15,-5), has a slope of -1/5. The segment above, connecting A(0,0) and C(16,2), has a slope of 1/8. Again, done.
Professor Greitzer, our Geometry kids may not understand anything about the radius of convergence of the Taylor series for the arctan function, but based on their exploring skills, we’re thinking that any mathematician of Dase’s era could have measured with a protractor, built a table, conjectured our conjectures, and built the coordinate plane arguments to verify that
$${{\pi}\over{4}}=\arctan{\frac{1}{2}}+\arctan{\frac{1}{3}}$$
and that
$$\arctan{\frac{1}{3}}=\arctan{\frac{1}{5}} +\arctan{\frac{1}{8}},$$
hence,
$${{\pi}\over{4}}=\arctan{\frac{1}{2}}+\arctan{\frac{1}{5}} +\arctan{\frac{1}{8}}\quad {\rm !}$$
so we conclude that the single exclamation mark identity is decidedly within the range of a mathematician (or a Geometry class), using only elementary mathematical tools. Cool, huh?