From ancient Greek times, mathematicians have considered three famous geometric construction problems. These problems are: (1) the duplication of the cube – construct the edge of a cube whose volume is twice that of a given cube; (2) the trisection of any angle – construct an angle that equals one-third of a given angle; and (3) the squaring of a circle – construct a square whose area equals the area of a given circle. Given the tools at the time, a compass and an unmarked ruler, these problems challenged mathematicians for centuries.

The best Greek intellect was bent upon them; Arabic learning was applied to them; some of the best mathematicians of the Western Renaissance wrestled with them.  Trained minds and untrained minds, wise men and cranks, all endeavoured to conquer these problems which the best brains of preceding ages had tried but failed to solve. (Cajori, 1924, p. 54)

Although these three problems are closely linked, we choose to examine the latter two problems. We must divulge that the given problems do not have solutions if we limit ourselves to constructions using only compass and straightedge. However, using curves created by other means the Greeks resolved all three problems.

            One of the most famous attempts to trisect an angle has been attributed to Hippias of Elis (born around 460 B.C.E.). He was a statesman and philosopher who traveled around being paid for his lectures on poetry, grammar, history, politics, archaeology, mathematics and astronomy. Plato described him as a vain man being both arrogant and boastful, having a wide but superficial knowledge (Burton, 2003 ). Hippias’ contribution to mathematics was small, but significant. In his attempt to trisect an angle, he created a new transcendental curve which unfortunately could not be constructed with only a compass and unmarked ruler; but the curve can be used to divide an angle into not only three, but any number of congruent angles. 

Hippias’ quadratrix was described as follows: “ABCD is a square and BED is part of a circle, centre A radius AB. As the radius AB rotates about A to move to the position AD then the line BC moves at the same rate parallel to itself [i.e., B′C′] to end at AD. Then the locus of the point of intersection F of the rotating radius AB [i.e., AE] and the moving line BC is the quadratrix” (from Book IV of Pappus' Synagoge circa 340) (see Figure 1).

Figure 1:  Quadratrix of Hippias

To construct the quadratrix using Geometer’s Sketchpad, you will first need to construct a square, ABCD, in your sketch window. Select any point on CD and call it C'. Construct a parallel line to BC, through the point C'.  Name the point of intersection of AB and the parallel line point B'. Construct the segment B'C'  and hide the line B'C'  (see Figure 2).

Figure 2:  Construction of the Quadratrix

Construct the circle with center A and radius AB. Next, construct arc BXD by identifying a point on the circle inside the square (point X). Then select, in order, points B, X, D and choose Arc Through 3 Points under the Construct menu (see Figure 3).

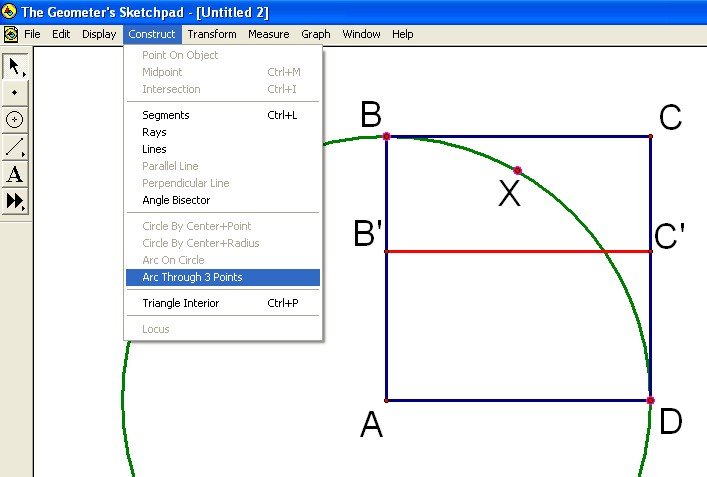
Figure 3:  Continuing the Construction of the Quadratrix by Constructing Arc BXD.

Hide circle A and point X. Now we want to place a point on arc BXD (point E) and construct AE. Lastly, construct the intersection of AE and B'C', and name the point of intersection F. Trace point F by selecting it and choosing Trace Intersection under the Display menu (see Figure 4).

Figure 4:  Continuing the Construction of the Quadratrix: Tracing Intersection Point F

The quadratrix is formed by point F as point C' moves along CD and point E moves along arc BED.  Since arc BED is longer than CD, we must calibrate the animation speed so that point C' takes exactly the same amount of time to traverse CD as point E takes to traverse arc BED. To do this calculate the ratio of the length arc BED to the length of CD. Use this ratio as the speed of the animation of point E and enter a speed of 1 for point C' by first selecting points E and C'; under the Edit menu select Action Buttons and then Animation (see Figure 5).

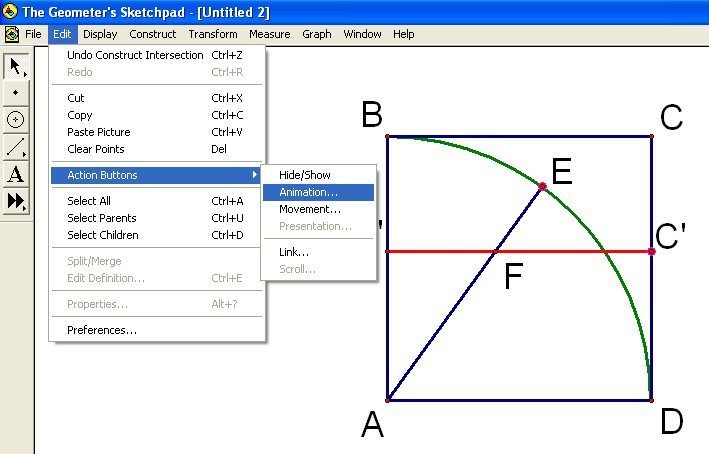
Figure 5: Animating Two Ponts Simultaneously with Geometer's Sketchpad.

Match the properties of each animation to those in figures 6 and 7.

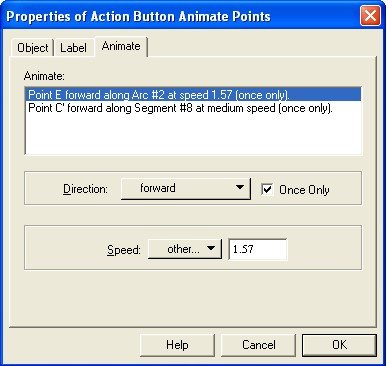
Figure 6:  Animation Properties of Point E

Figure 7:  Animation Properties of Point C'

You will also want to construct a movement button to “reset” the sketch. In order to do this select the following points in order E, B, C' and C, then Action Buttons, then Movement under the Edit menu (see Figures 8 and 9).  

Figure 8:  Constructing a Movement Button to "Reset" Your Sketch

Figure 9:  Properties of the Movement Button

Click on the movement button to reset the sketch, press the Esc button twice to erase any traces in your sketch window, and click on the Animation button to activate the animation.  Click here  to see the animation. The locus of point F is called the “Quadratrix of Hippias”.

Once the quadratrix has been formed, move point E anywhere along arc BED. Using Hippias’ method, we will find an angle one-third the measure of angle DAE. Move points C' and E such that point F is the intersection of the quadratrix and AE (see Figure 10).

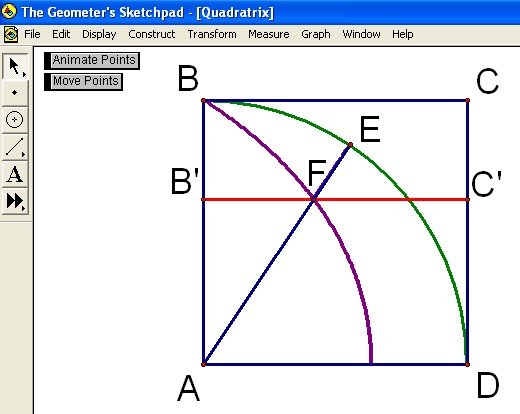
Figure 10: Using the Quadratrix To Trisect Angle DAE

Construct a perpendicular line to AD through the point F. Construct the intersection point of this perpendicular line and segment AD and label it H. Next construct segment FH and hide line FH. The trisection of an angle has now been reduced to trisecting the line segment FH. Formally construct a point (K) along FH such that HK is one-third the length of FH.  Click here  to see the animation of this construction.

Construct a parallel line to AD through point K. Identify the intersection of the parallel line with the quadratrix, and name this point J. Construct ray AJ.  The measure of angle DAJ is one-third the measure of angle DAE (see Figure 11).

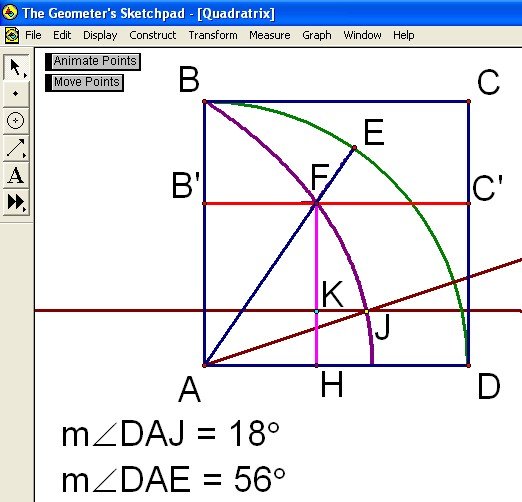
Figure 11:  Using the Quadratrix to Trisect Angle DAE

As one can see, the quadratrix can be used to easily reduce the problem of trisecting an angle to that of trisecting a line segment; furthermore Hippias generalized this method to subdivide any given angle into any number of equal subangles.

Although many scholars attempted to trisect an angle, the more popular construction of the three famous geometric construction problems was to find a square with the same area as a given circle. Hippocrates of Chios made major contributions toward mathematics while trying to solve this problem.

Hippocrates of Chios  (born around 470 B.C.E.), not to be mistaken for Hippocrates of Cos who is the father of Greek medicine, focused much of his studies on solving the three constructions of Greek Antiquity. Although little is known about Hippocrates’ life, it is thought that he traveled from the Island of Chios to Athens to settle a lawsuit in connection with either being deceived by customhouse officers at Byzantium or having his ships looted by pirates. While settling the court issue whose outcome is unknown, Hippocrates attended lectures of Athenian scholars, provoking his interest in solving the three classical problems of Greek Antiquity. Heath notes that Hippocrates had three main contributions to mathematics:

• He was, so far as we know, the first to compile a book of Elements.
• In an attempt to square the circle he showed how to square certain classes of ‘lunes’.
• He was the first to observe that the problem of doubling the cube can be reduced to that of finding two mean proportionals in continued proportion between two given straight lines, with the result that the problem was ever afterwards attacked in the latter form. (Heath, 1963, p. 121)

As described in his second accomplishment, Hippocrates calculated the area of different types of lunes, which are regions between arcs of two circles as shown in figure 12, in his attempt to construct a square with the same area as a circle. Hippocrates calculated the area of three types of lunes, that is, a lune with an outer arc greater than a semicircle, one with an outer arc less than a semicircle, and one with an outer arc equal to a semicircle.

Figure 12:  Examples of lunes.

It should be noted that Hippocrates was well aware of properties of circles, in particular that the areas of two circles are proportional to the squares on their diameters. In addition, he knew the Pythagoreans had shown that the sum of the square areas on two legs of a right triangle is equal to the square area on the hypotenuse. With this in mind, we begin interpreting Hippocrates’ method for calculating the area of a lune with an outer arc equal to a semicircle and share how to use Geometer’s Sketchpad to explore this proof.

What follows is Heath’s details of Eudemus’s description of Hippocrates’ method for calculating the area of one type of lune (see Figure 13 for an example of Hippocrates’ lune).

After proving this, he proceeded to show in what way it was possible to square a lune the outer circumference of which is that of a semicircle. This he effected by circumscribing a semicircle about an isosceles right-angled triangle and (circumscribing) about the base a segment of a circle similar to those cut off by the sides. Then, since the segment about the base is equal to the sum of those about the sides, it follows that, when the part of the triangle above the segment about the base is added to both alike, the lune will be equal to the triangle. Therefore the lune, having been proved equal to the triangle, can be squared. In this way, assuming that the outer circumference of the lune is that of a semicircle, Hippocrates easily squared the lune  (Heath, 1921, pp. 191-192).

Figure 13: The area shaded in black is an example of Hippocrates’ lune.

Since Heath noted that Hippocrates was initially “circumscribing a semicircle about an isosceles right-angled triangle”, it is necessary to begin by constructing an isosceles right-angled triangle as shown in figure 14.

Figure 14:  Isosceles right triangle ABC circumscribed by semicircle ABC.

An isosceles-right triangle could also have been constructed using points A, C, and D (see Figure 15). Therefore, AB = BC = CD = DA.

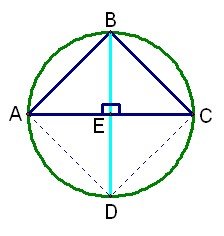
Figure 15: Construction of isosceles right triangle ABC.

Next, we construct a second circle with center D and radius DA to get “a segment of a circle similar to those cut off by the sides” of the isosceles right triangle  ABC (see Figure 16). This segment of a circle with base AEC is in a quadrant of a circle and is therefore similar to the two original segments with base AB and BC.

Figure 16:  Construction of a circle with center D.

Next,  “the segment about the base” is the segment bounded by arc AHC and chord AEC. That this segment “is equal to the sum of those about the sides” of triangle ABC follows from a generalization of the Pythagorean theorem, that if similar figures are constructed on the hypotenuse and the two legs of a right triangle, the area of the figure on the hypotenuse is the sum of the areas of the figures on the legs. This theorem can be verified by constructing and measuring these three areas. To construct the segment bounded by arc AHC and chord AEC, select points A, H, and C in that order or in the reverse order. Then select Arc Through 3 Points from the Construct menu. With arc AHC highlighted, select, from the Construct menu, Construct Arc Interior and then Arc Segment. With the arc segment highlighted, select Area from the Measure menu. A similar process can be followed to construct and measure the segment bounded by arc AIB and chord AB and by are BJC and chord BC whose areas can then be summed.  You can click here  to see this construction.  Also, see Figure 17.

Figure 17. Arc segments AHC, AIB, and BJC.

We can then use the dynamic capabilities of Geometer’s Sketchpad to verify that the segment bounded by arc AHC and chord AEC is the sum of the areas of the segments bounded by arc AIB and chord AB and by are BJC and chord BC. This is done by clicking and dragging one of the two points that define circle E, which is either point E or point A in this example, and noticing that this is always true.

            Hippocrates then stated, “it follows that, when the part of the triangle above the segment about the base is added to both” the segment AHCE, which gives the triangle ABC, and the two segments in pink, which gives the lune, “the lune will be equal to the triangle”. 

Although this is quite clear from the diagram, we will demonstrate it algebraically as well.  Let the length of each leg of triangle ABC equal x. Therefore, the hypotenuse of triangle ABC, which is the diameter of the smaller circle (circle E), is x Ö2. Since the larger circle (circle D) has a diameter of 2x, the ratio of the diameter of the larger circle to the smaller circle is (2x)² /(x Ö2)² = 4x²/2x² = 2/1. Therefore, the area of circle D is twice the area of circle E. It follows that the area of any part of circle D is also twice that of an analogous part of circle E, which proves that the segment on base AEC is double each of the two segments in circle E.

            Although Hippocrates fell short of squaring a circle, he was the first to compare the area of a curvilinear figure to that of a rectilinear figure. As a result of squaring the area of a lune, Hippocrates was the first to show that figures with curved boundaries could be squared.

Although the three famous geometric construction problems are closely linked, we choose to deeply examine the trisection of an angle and the quadrature of the square with the use of dynamic geometry software. The dynamic capabilities of Sketchpad allow a user to analyze endless representations of trisecting an angle and calculating the area of a lune. Having opportunities to dynamically investigate these constructions may be extremely beneficial for students to visualize the construction beyond one static example to multiple dynamic examples. 

References

Burton, D.A. (2003). The history of mathematics: An introduction (5th ed.). New York: McGraw-Hill.

Cajori, F. (1924). A history of elementary mathematics with hints on methods of teaching. Rev. and enl. Ed. New York: MacMillan.

Heath, T.L. (1921). A History of Greek Mathematics (vol. 1). New York: Oxford University Press.

Heath, T.L. (1963). Greek mathematics. New York: Dover.