Intuitively a set S in the plane is connected if for every pair of distinct points p₁ = (x₁,y₁) and p₂ = (x₂,y₂) and in S there is a curve consisting of points in S with endpoints p₁ and p₂.  This definition was sufficient until the end of the nineteenth century, when an implosion of imaginative examples of curves in the plane demanded a more rigorous definition.  One purpose of this paper is to trace this aspect of the early history of connected sets based on the formal definition that replaced the intuitive one.  To illustrate the need for such a rigorous definition, we introduce a curve called Mullikin’s nautilus that was first constructed in 1919.  Since the formal definition relies on limit points, the nautilus not only illustrates its necessity but serves as an instructive vehicle for introducing limits in the plane to students who have studied limits on the real line.  Therefore the second purpose of this paper is to present material directly applicable to the classroom.

In October 1919 the renowned mathematician R. L. Moore read a paper written by his third doctoral student Anna M. Mullikin before an AMS meeting at Columbia University in New York City.  Titled “A countable collection of mutually exclusive closed point sets with connected sum,” it presented a clever yet fairly simple example that Miss Mullikin constructed during her first year under Moore’s tutelage at the University of Pennsylvania [1, pp. 146-147].  Ultimately the example, which has come to be known as “Mullikin’s nautilus,” constituted the first part of Mullikin’s doctoral dissertation, which was published in the Transactions three years after her first AMS presentation [3].

Mullikin’s nautilus consists of an infinite collection of arcs M_n, for n = 1, 2, 3, … , each composed of four line segments drawn from the x-intercept (1/2^n-1, 0) to (1/2^n-1, 1/2^n-1) , thence to (-1/2^n-1, 1/2^n-1) and (-1/2^n-1, -1/2^n-1), and finally to (1, -1/2^n-1) .  The abscissa of the final point is always x = 1.  Figure 1, taken from Mullikin’s dissertation, displays the first three color-coded arcs: M₁, M₂, and M₃.  Formally, Mullikin’s nautilus is defined as M = U M_n.

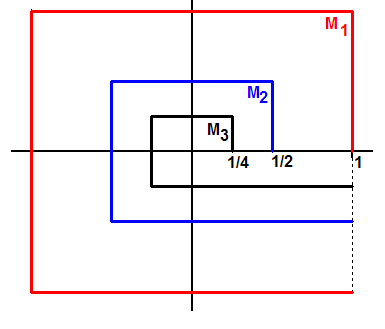
Figure 1

Clearly each arc is connected, but the union M₁U M₂ U M₃ is not.  In Figure 1, for instance, the point (1, -1) on M₁ cannot be connected to the point (1, -1/4) on M₃. We pose the following

FUNDAMENTAL QUESTION: Is Mullikin’s nautilus M = U M_n connected?

The reader might want to hazard a guess now.  [Disclosure: this is not an easy issue to resolve.]  The answer will be divulged shortly.

In order to answer the Fundamental Question, it is necessary to formulate a definition of connected sets that captures the intuitive notion of continuity in a rigorous and applicable manner.  To accomplish this we need two preliminary definitions.  First, the closure of a set X, denoted by `X, consists of X and all of its limit points.  Then we say that two distinct sets A and B are separated if neither contains a limit point of the other, that is, if A Ç`B = f and A Ç B = f.  For instance, the upper half-plane and lower half-plane are separated.  We are now poised to state the definition of connected sets first proposed by the Norwegian-born American mathematician Nels J. Lennes [2].

FUNDAMENTAL DEFINITION: A set of points is connected if it cannot be written as the union of two separated sets.

At heart, this definition expresses connectedness in terms of limit points, so to gain insight into Mullikin’s nautilus we restate an assertion Miss Mullikin made.

MULLIKIN’S LEMMA: Each arc M_j contains a limit point of every subset of M which consists of an infinite number of the remaining arcs.

In Mullikin’s Lemma, the intercept x_j = (1/2^j-1, 0) is a point on the arc  M_j  that is a limit point of every subset of M consisting of an infinite number of the remaining arcs.  Click here to see a QuickTime movie demonstrating the convergence geometrically for x₃ = (1/4, 0).

An understanding of this movie permits one to form the closure `M of Mullikin’s nautilus M = U M<sub>n</sub>.  For if  p = (x, 0) with 0 £ x £ 1, then p Î`M.    Hence `M = M U I, where I is the unit interval in the plane.  Click here to see a QuickTime movie demonstrating this convergence for x = 1/3.  Since (1/3, 0) is in`M  but not in M, it follows that M is not closed.

In the official report from the AMS meeting where Mullikin’s paper was read, longtime Society secretary Frank N. Cole reported, “In one dimension no countably infinite collection of mutually exclusive closed point sets ever has a connected sum.  One might rather naturally be inclined to believe that this proposition holds true also in two dimensions.  Miss Mullikin shows by an example that this is, however, not the case” [1, p. 147].  Mullikin expressed her motivation somewhat differently in the introduction to her dissertation.  After citing Lennes’ formulation of a connected set, she stated Sierpinski’s Theorem that a closed, bounded, and connected set in n dimensions cannot be written as a disjoint union of a countable number of closed sets.  Now, each arc in the Mullikin nautilus M = U M_n is obviously closed, and the set M is clearly bounded.  Mullikin asserted that M is also connected, which thus achieved her goal.  She wrote, “It will be shown in the present paper that for the case where n = 2, this theorem [of Sierpinski] does not remain true if the stipulation that M is closed be removed” [3, 144].

Mullikin’s Theorem: The nautilus  is connected.

Proof.  Suppose M is the union of separated sets A and B.  Then each arc M_n = A_n U B_n, where A_n=A Ç M_n and B_n=B Ç M_n.  But M_n is connected, so either  M_n = A_n  or M_n = B_n .  Therefore A and B are collections of arcs.  One of these collections must be an infinite set, say A.  By Mullikin’s Lemma, if B consists of at least one arc then it will contain a limit point of A, contradicting the assumption that A and B are separated.  Consequently B = f, hence M is connected.

Armed with an intuitive feel for limit points of the nautilus, the fact that M is connected can be underscored by viewing a QuickTime movie whose dynamics reinforce Mullikin’s Theorem.  Click here to view it.  A module for presenting this in the classroom can be obtained at the Math Gateway partner “Demos with Positive Impact” by clicking  here.

1.  Cole, F. N., The October meeting of the American Mathematical Society, Bull. Amer.  Math. Soc. 26 (1919) 145-151.

2.  Lennes, N. J., Curves in non-metrical analysis situs, Bull. Amer. Math. Soc. 12 (1905-1906) 284.

3.  Mullikin, Anna M., Certain theorems relating to plane connected point sets, Trans. Amer. Math. Soc. 24 (1922) 144-162.