Proportionality in Similar Triangles: A Cross-Cultural Comparison
A fundamental result of geometry, used often in secondary and collegiate mathematics, is the equality of ratios of corresponding sides in similar triangles. This concept is expected knowledge of students in physics, engineering, and the sciences, since its simple statement is rather useful in finding unknown lengths of elementary figures in plane geometry. Why does this geometric result hold? What do we teach our students about this relation, and, more importantly, how is this result presented to secondary education majors, who will be teaching future college students? Is the result justified by an appeal to reason, or are similar triangles defined as those triangles for which corresponding sides have equal ratios? Both of these approaches are found in today's curriculum, although neither is particularly revealing.
This article offers curricular materials for the proof of similarity theorems, based on an ancient Chinese principle of area known as the "in-out" or "inclusion-exclusion" principle. When applied to a rectangle, the principle identifies certain (non-congruent) sub-rectangles of equal area that remain after the exclusion of congruent triangles. The principle is easily applied when the excluded triangles are right triangles, and to account for all possible pairs of corresponding sides in a right triangle, further application of the gou-gu (Pythagorean) theorem is used. Another engaging use of the inclusion-exclusion principle is the proof of the gou-gu theorem itself, borrowing an idea from the text Zhou bi suan jing (Mathematical Classic of the Zhou Gnomon) [5], compiled between 100 BCE and 100 CE. Strictly speaking gou refers to base or shadow and gu refers to height or gnomon, although there apparently was no word per se for the concept of a triangle in ancient China [5, p. 215]. See Mathematics in China <http://aleph0.clarku.edu/~djoyce/mathhist/china.html> at David Joyce's Mathematics History website <http://aleph0.clarku.edu/~djoyce/mathhist/> for further information about the history of Chinese mathematics.
Since teaching similarity results from ancient Chinese principles of reasoning may be novel to many instructors, the article begins with Euclid's classical approach to the subject. Although ideas of reasoning and a concept of rigor differ between the Chinese and Greek schools of mathematical thought, similarity results for both cultures rest ultimately on two-dimensional area arguments. A latent mathematical axiom behind any similarity result is the parallel postulate, a subtle axiom with implications impinging on many constructions and theorems in geometry. The existence of a rectangle itself, not to mention a formula for its area, is logically equivalent to the Euclidean parallel postulate [2]. Likewise the expression of the area of a triangle as one-half the base times the height is a Euclidean formula, since it relies on the area result of an enveloping rectangle or parallelogram. Euclid's proof of similarity results relies on proposition 38 from book I of The Elements [1]:
I.38. Triangles which are on equal bases and in the same parallels are equal to one another.
Given triangle ABC with side AB identified as the base, there is only one line through C parallel to AB, thus determining the height of the triangle. Proposition I.38 asserts that two triangles with equal bases and equal heights will in fact have equal area. Another result equivalent to the Euclidean parallel postulate is the theorem stating that any triangle has angle sum 180° [2], which is in turn equivalent to a rectangle having angle sum 360°. The web resource Non-Euclidean Geometry <http://www-history.mcs.st-and.ac.uk/HistTopics/Non-Euclidean_geometry.html> at the MacTutor History of Mathematics Archive <http://www-history.mcs.st-and.ac.uk> offers further history of the parallel postulate.
While Euclid follows a step-by-step model of deductive reasoning with every statement justified by a previous proposition, definition, or postulate, the Chinese method is a bit more intuitive, particularly when identifying what today would be called congruent triangles. The ease by which similarity results are then proven (as a modern exercise) is appealing. Moreover, the argument founded on Chinese principles does not require a comparison of possibly two incommensurable lengths for the bases in similar triangles, as Euclid must consider. Two lengths L1, L2 are commensurable if a whole-number multiple of L1 can be constructed on a whole-number multiple of L2, or in modern language [3, p. 30], if there are positive integers n1, n2 with n1 L1 = n2 L2, or equivalently, [(L1)/(L2)] is a rational number. See the web resource Greek Mathematics <http://www-history.mcs.st-and.ac.uk/Indexes/Greeks.html> at the MacTutor History of Mathematics Archive <http://www-history.mcs.st-and.ac.uk> for detailed information about the history of Greek mathematics.
The curricular presented materials in Section 4 are ideal for a course in geometry, taught either in college or high-school, or for a course that draws prospective teachers of secondary mathematics. For use in the classroom, the instructor should present the results of Section 3, although Section 2 may be omitted from class discussion, depending on course direction and time constraints. When assigning the material in class, the instructor may delete or rearrange certain parts of the teaching module to fit the course.
Proportionality in Similar Triangles: A Cross-Cultural Comparison - Introduction
A fundamental result of geometry, used often in secondary and collegiate mathematics, is the equality of ratios of corresponding sides in similar triangles. This concept is expected knowledge of students in physics, engineering, and the sciences, since its simple statement is rather useful in finding unknown lengths of elementary figures in plane geometry. Why does this geometric result hold? What do we teach our students about this relation, and, more importantly, how is this result presented to secondary education majors, who will be teaching future college students? Is the result justified by an appeal to reason, or are similar triangles defined as those triangles for which corresponding sides have equal ratios? Both of these approaches are found in today's curriculum, although neither is particularly revealing.
This article offers curricular materials for the proof of similarity theorems, based on an ancient Chinese principle of area known as the "in-out" or "inclusion-exclusion" principle. When applied to a rectangle, the principle identifies certain (non-congruent) sub-rectangles of equal area that remain after the exclusion of congruent triangles. The principle is easily applied when the excluded triangles are right triangles, and to account for all possible pairs of corresponding sides in a right triangle, further application of the gou-gu (Pythagorean) theorem is used. Another engaging use of the inclusion-exclusion principle is the proof of the gou-gu theorem itself, borrowing an idea from the text Zhou bi suan jing (Mathematical Classic of the Zhou Gnomon) [5], compiled between 100 BCE and 100 CE. Strictly speaking gou refers to base or shadow and gu refers to height or gnomon, although there apparently was no word per se for the concept of a triangle in ancient China [5, p. 215]. See Mathematics in China <http://aleph0.clarku.edu/~djoyce/mathhist/china.html> at David Joyce's Mathematics History website <http://aleph0.clarku.edu/~djoyce/mathhist/> for further information about the history of Chinese mathematics.
Since teaching similarity results from ancient Chinese principles of reasoning may be novel to many instructors, the article begins with Euclid's classical approach to the subject. Although ideas of reasoning and a concept of rigor differ between the Chinese and Greek schools of mathematical thought, similarity results for both cultures rest ultimately on two-dimensional area arguments. A latent mathematical axiom behind any similarity result is the parallel postulate, a subtle axiom with implications impinging on many constructions and theorems in geometry. The existence of a rectangle itself, not to mention a formula for its area, is logically equivalent to the Euclidean parallel postulate [2]. Likewise the expression of the area of a triangle as one-half the base times the height is a Euclidean formula, since it relies on the area result of an enveloping rectangle or parallelogram. Euclid's proof of similarity results relies on proposition 38 from book I of The Elements [1]:
I.38. Triangles which are on equal bases and in the same parallels are equal to one another.
Given triangle ABC with side AB identified as the base, there is only one line through C parallel to AB, thus determining the height of the triangle. Proposition I.38 asserts that two triangles with equal bases and equal heights will in fact have equal area. Another result equivalent to the Euclidean parallel postulate is the theorem stating that any triangle has angle sum 180° [2], which is in turn equivalent to a rectangle having angle sum 360°. The web resource Non-Euclidean Geometry <http://www-history.mcs.st-and.ac.uk/HistTopics/Non-Euclidean_geometry.html> at the MacTutor History of Mathematics Archive <http://www-history.mcs.st-and.ac.uk> offers further history of the parallel postulate.
While Euclid follows a step-by-step model of deductive reasoning with every statement justified by a previous proposition, definition, or postulate, the Chinese method is a bit more intuitive, particularly when identifying what today would be called congruent triangles. The ease by which similarity results are then proven (as a modern exercise) is appealing. Moreover, the argument founded on Chinese principles does not require a comparison of possibly two incommensurable lengths for the bases in similar triangles, as Euclid must consider. Two lengths L1, L2 are commensurable if a whole-number multiple of L1 can be constructed on a whole-number multiple of L2, or in modern language [3, p. 30], if there are positive integers n1, n2 with n1 L1 = n2 L2, or equivalently, [(L1)/(L2)] is a rational number. See the web resource Greek Mathematics <http://www-history.mcs.st-and.ac.uk/Indexes/Greeks.html> at the MacTutor History of Mathematics Archive <http://www-history.mcs.st-and.ac.uk> for detailed information about the history of Greek mathematics.
The curricular presented materials in Section 4 are ideal for a course in geometry, taught either in college or high-school, or for a course that draws prospective teachers of secondary mathematics. For use in the classroom, the instructor should present the results of Section 3, although Section 2 may be omitted from class discussion, depending on course direction and time constraints. When assigning the material in class, the instructor may delete or rearrange certain parts of the teaching module to fit the course.
Proportionality in Similar Triangles: A Cross-Cultural Comparison - The Ancient Greek Contribution
Similarity has its roots in antiquity, and ideas of proportion were likely known to the Pythagoreans in the fifth century [4, p. 82-83], while Eudoxus of Cnidus (ca. 408-355 ) established a notion of what today would be called the equality of ratios [3, p. 28], crucial in the case of incommensurable magnitudes. Euclid (third century ) devotes Book V of The Elements to a study of proportion, incorporating many of the ideas developed earlier in ancient Greece, particularly those practiced by Pythagoras and Eudoxus. Proposition Four in Book VI of The Elements [1] states:
VI.4. In equiangular triangles the sides about the equal angles are proportional, and those are corresponding sides which subtend the equal angles.
In a model of deductive reasoning, Euclid proves this statement, which relies on propositions VI.2, VI.1, Book V, and ultimately on Book I for constructions in Euclidean geometry. To provide the reader with a sense of development for VI.4, and a glimpse into the ideas behind the result, here are the propositions VI.2 and VI.1, in reverse order as presented in The Elements [1].
VI.2. If a straight line be drawn parallel to one of the sides of a triangle, it will cut the sides of the triangle proportionally; and [conversely].
VI.1. Triangles and parallelograms which are under the same height are to one another as their bases.
Height here refers to perpendicular height, and by the ratio of two triangles "to one another" is meant the ratio of their areas. In modern parlance, VI.1 states that the ratio of the area of two triangles with the same height is equal to the ratio of their bases, and this result also holds for parallelograms. For triangles with commensurable bases, Euclid's proof of VI.1 begins by constructing whole number multiples of the two bases to arrive at two triangles with equal bases. The result then follows from I.38, discussed in the introduction. Issues of incommensurability are addressed via the Eudoxan theory of proportion.

Figure 1: Proposition VI.2.
To prove VI.2, Euclid begins with triangle ABC (not necessarily isosceles) and constructs DE parallel to BC (Figure 1). Note that triangles DEB and DEC have the same area, since they are on the same base DE and are in the same parallels (between DE and BC). It follows that triangle ABE and triangle ACD have the same area. A modern interpretation of Euclid would read
| Area (triangle ABE)
|
= | Area (triangle ACD)
|
. |
Since triangles ABE and DEB are under the same height, they are to one another as their bases, and similarly for triangle ACD and triangle DEC. Thus,
|
It follows that AB/DB = AC/EC.

Figure 2: Proposition VI.4.
To prove VI.4 quickly, begin with similar triangles ABC and DEF and construct triangle DEF inside triangle ABC along a congruent pair of angles (Figure 2). The result then follows from Proposition VI.2, and a general position argument stating that triangle DEF could be constructed inside triangle ABC along any pair of congruent angles. Euclid, however, avoids a general argument in favor of a more literal proof. (See [1]).
Proportionality in Similar Triangles: A Cross-Cultural Comparison - The Ancient Chinese Contribution
Ancient Chinese mathematics was often used to meet the imperial needs of engineering, land mensuration, calendar reckoning, military campaigns, and water control and conservancy [5, 7]. The oldest extant Chinese mathematical treatise, the Zhou bi suan jing (Mathematical Classic of the Zhou Gnomon), written around 100 BCE - 100 CE , is devoted primarily to astronomical and calendrical matters. The title of this work has also been translated as The Arithmetical Classic of the Gnomon and Circular Paths of Heaven, while astronomers themselves in China were dubbed "surveyors of the heavens." The text contains results on right triangles, such as gou-gu relations, and discusses the use of measuring instruments, such as the L-shaped set-square or gnomon. This device along with appropriate measurements and proportionality results for similar triangles allowed the determination of distances to inaccessible points [7].
The practice of mathematics in ancient China acquired a mythical, if not a purely utilitarian status. The legendary emperor-engineer Yu the Great, depicted holding a set-square, is claimed to have accomplished much via the use of mathematics:
Emperor Yu quells the floods, he deepens the rivers and streams, observes the shape of mountains and valleys, surveys the high and low places, relieves the greatest of calamities and saves the people from danger. He leads the floods east into the sea and insures no flooding or drowning. This is made possible because of the gou-gu theorem [8, p. 29-30].
A second classic, the Jiu zhang suan shu (The Nine Chapters on the Mathematical Art), is a compilation of mathematical techniques known or developed between the eleventh century BCE and 220 CE. More of a reference manual or study guide, the text contain 246 problems ranging from computing with fractions to finding the area of rectangular fields to applications of the gou-gu relation. The third century scholar, Liu Hui, sometimes referred to as "the Chinese Euclid," compiled an edition of the Jiu zhang suan shu that became rather influential in China, and was used at the Imperial College during the Tang dynasty (618-907) [5, p. 227].
Additionally and significantly, Liu authored the Hai dao suan jing (The Sea Island Mathematical Manual) [7], which was written as an addendum to the Jiu zhang suan shu, but eventually appeared separately. Recognized as an original contribution to the art of surveying, the Hai dao suan jing develops a method of determining the height of an unknown object based on sightings from two poles of equal (known) height, a fixed distance apart, that was applied to computing such fanciful calculations as the height of the sun. The method, called chong cha or "double difference" can be used to find the height PQ given the lengths AS = CN (the "poles"), SB, ND (the "shadows"), and SN below (Figure 3). The result PQ is expressed in terms of the height AS and the two differences ND - SB and QN - QS = SN, so that the actual distances of S and N from the point Q need not be known, as long as the distance between the poles, SN, is known. The verification requires two applications of proportionality results for similar triangles (see Extra Credit A of Section 4.)
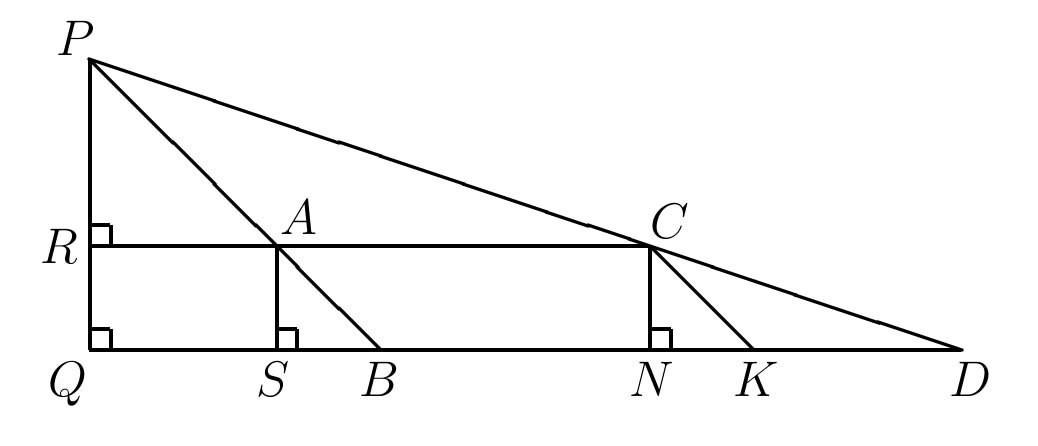
Figure 3: The Chong Cha Method
Let's examine an area argument appearing in the Zhou bi suan jing and the Jiu Zhang suan shu referred to as the "in-out" principle [5] or the "inclusion-exclusion" principle. This may be interpreted as a duality statement, where one part of a figure corresponds to an often congruent dual or counterpart in the same figure. Consider rectangle ABCD with diagonal BD (Figure 4).
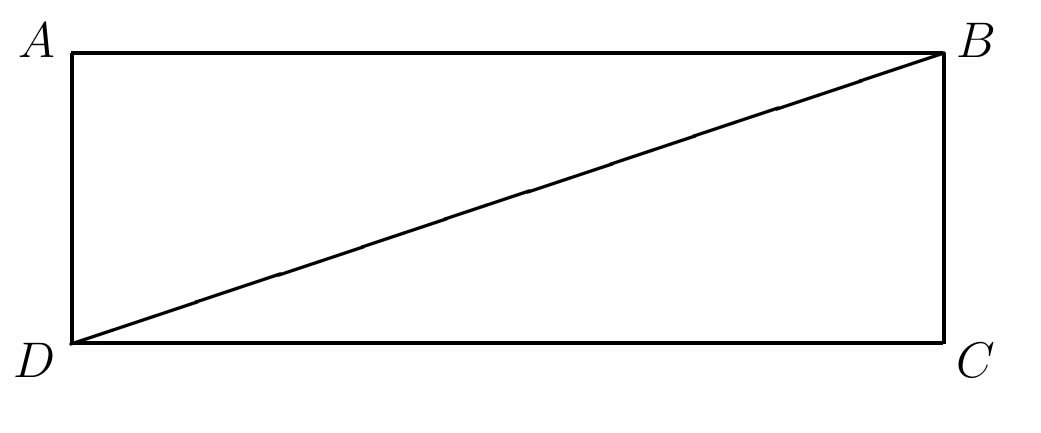
Figure 4: Rectangle ABCD.
Then triangles ABD and CDB have the same area, since they are congruent. On the diagonal BD choose a point H, and draw JK through H parallel to AB, and draw LM through H parallel to BC. The inclusion-exclusion principle states that figures \(III\) and \(III^{\prime},\) i.e. rectangles ALHJ and HKCM, have the same area (Figure 5).
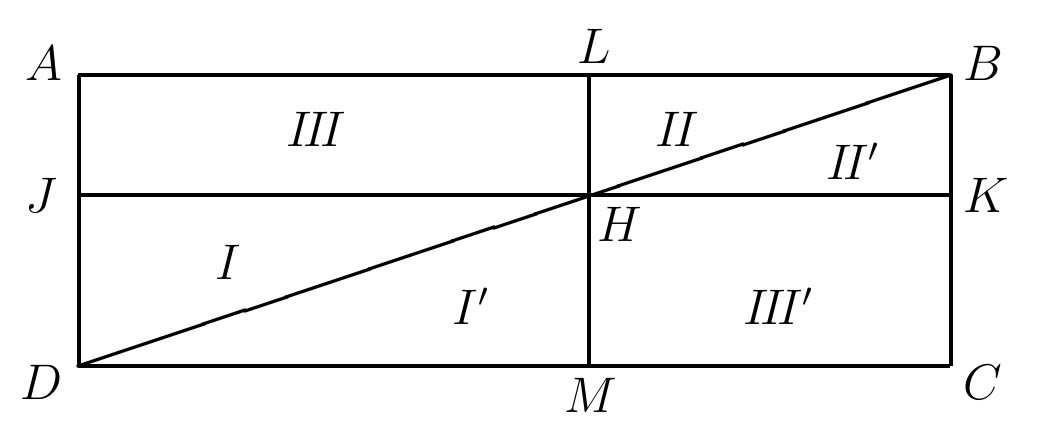
Figure 5: The "In-Out" Principle.
This follows since triangles \(I\) and \(I^{\prime}\) are congruent, and thus have the same area, while triangles \(II\) and \(II^{\prime}\) also have the same area. Deleting \(I\) and \(II\) from triangle ABD, and deleting \(I^{\prime}\) and \(II^{\prime}\) from triangle CDB, it follows that \(III\) and \(III^{\prime}\) have the same area.
Proportionality in Similar Triangles: A Cross-Cultural Comparison - The Student Module
What follows is a sequence of guided student exercises.
(a) Given similar right triangles ABC and DEF below, let b1 be the length of AB, b2 that of DE, h1 that of CB, and h2 that of FE (Figure 6).
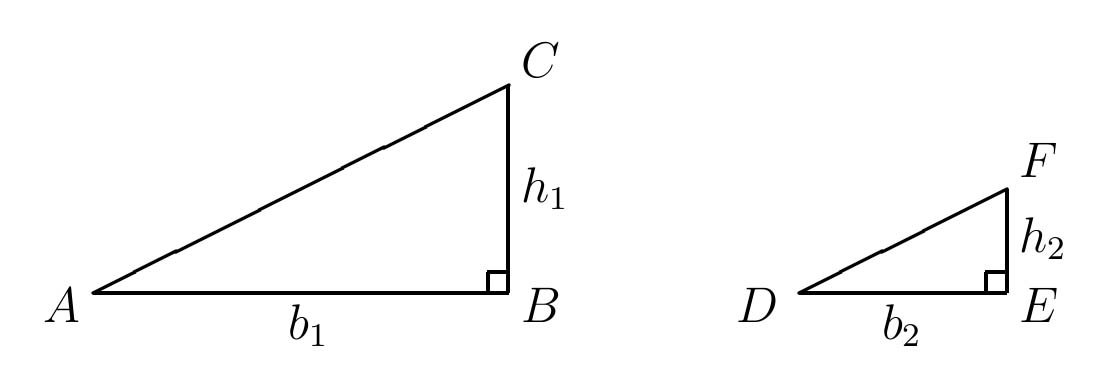
Figure 6: Similar Right Triangles.
By definition of similar triangles, ∠A \(\cong\) ∠D, ∠B \(\cong\) ∠E, ∠C \(\cong\) ∠F. For part (a), consider as given that both ∠B and ∠E are right angles. Prove that
|
by the following outline. Place point D on point C so that the points A, C, and F are collinear (Figure 7).
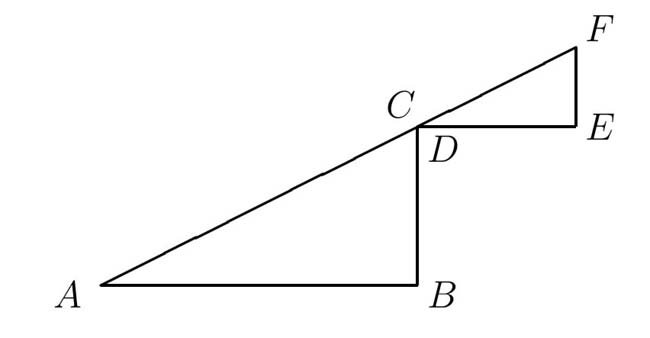
Figure 7: Arrangement of the Triangles.
Duplicate triangle ABC to form triangle AJC, and duplicate triangle DEF to form triangle DLF, pictured below (Figure 8).
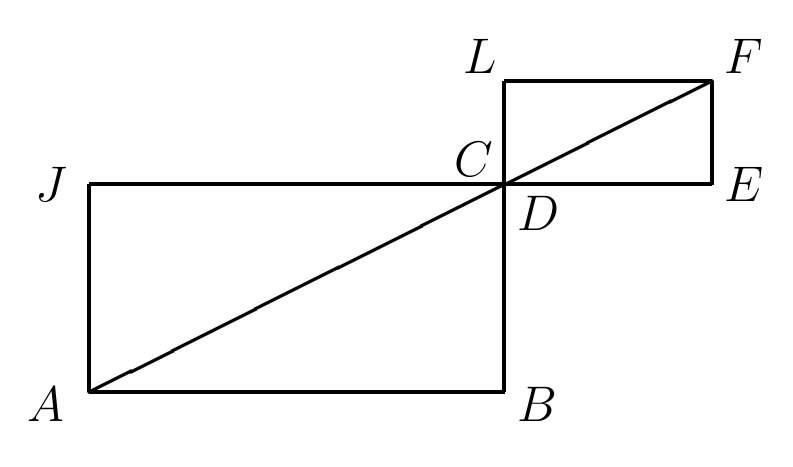
Figure 8: The Duplicated Triangles.
Why are ∠JAB and ∠EFL both right angles? Explain why lines AJ and FL, if extended, will meet in a right angle. Also, explain why lines AB and FE, if extended, will meet in a right angle. Let K and M be these two points of intersection, respectively. Sketch the resulting rectangle AKFM, and apply the inclusion-exclusion principle to find an algebraic expression for the area of the sub-rectangles KLCJ and DEMB in terms of b1, b2, h1, h2. What can be concluded from the resulting equation?
(b) In triangle ABC and triangle DEF (Figure 6) let d1 be the length of AC and d2 the length of DF. Use the gou-gu (Pythagorean) theorem and the result of part (a) to prove algebraically that
|
(c) Develop a version of the inclusion-exclusion principle that applies to an arbitrary parallelogram ABCD (Figure 9).

Figure 9: Parallelogram ABCD .
Begin by constructing diagonal DB and choosing a point H along the diagonal.
(d) Let triangle ABC and triangle DEF be arbitrary similar triangles (not necessarily right triangles) with ∠A \(\cong\) ∠D, ∠B \(\cong\) ∠E, ∠C \(\cong\) ∠F (Figure 10).
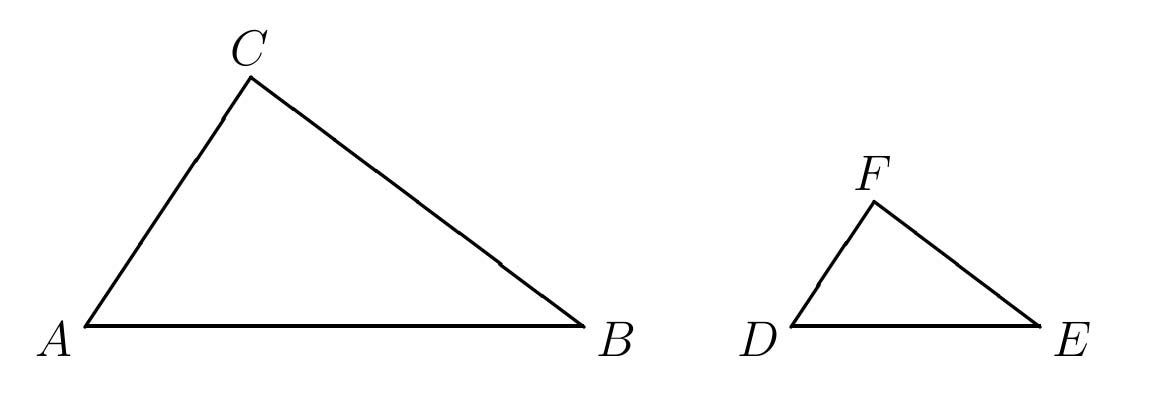
Figure 10: Arbitrary Similar Triangles.
Let b1 be the length of AB, b2 the length of DE, s1 the length of CB, and s2 the length of FE. Prove that
|
using either of the strategies below.
1. Apply the inclusion-exclusion principle for an arbitrary parallelogram. What happens if triangle ABC and triangle DEF are acute triangles? obtuse triangles?
(e) Prove the gou-gu (Pythagorean) theorem as another application of the inclusion-exclusion principle, following the footsteps of the ancient Chinese. Given right triangle ABC with ∠B a right angle, let a be the length of AB, b the length of CB, and c the length of AC. We wish to prove that
|
First consider the case of an isosceles right triangle, where a = b. By duplicating triangle ABC four times, construct square ACDE (Figure 11).

Figure 11: Square ACDE with a = b.
Explain why the area of this square is c2. Using the area of triangle ABC, explain why square ACDE also has area
|
Now consider right triangle ABC with b > a. Again construct square ACDE with side length c (Figure 12).
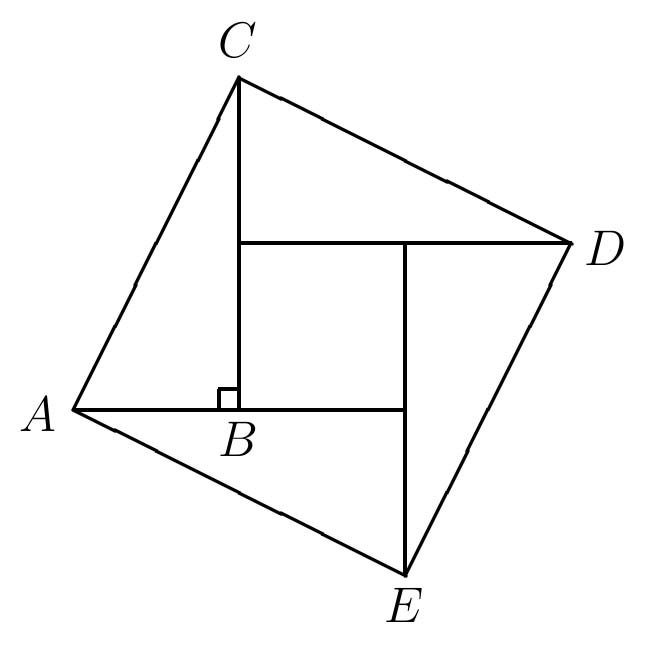
Figure 12: Square ACDE with b > a.
Explain why the inside square has side length b - a. By excluding this inside square from the outside square, find an expression for
|
using two methods, one algebraic, the other geometric in terms of the area of the four remaining triangles. What results after equating these two expressions?
Extra Credit A: Verify the chong cha method by demonstrating that in Figure 3, we have
|
where h is the length of AS, d the length of SN, a1 the length of SB, and a2 the length of ND. Hint: Draw line CK parallel to AB, and consider two pairs of similar triangles, triangles PRA and ASB and triangles PAC and CKD.
Extra Credit B: Read and study Proposition I.43 from the first book of Euclid's Elements. Compare Euclid's use of rigor in the proof of I.43 to the more intuitive application of the "in-out" principle for the rectangle in Figure 5. Speculate why Euclid did not use I.43 to prove VI.4. What may have prevented the ancient Greeks from developing an algebra of real numbers that would have allowed the transfer of results like I.43 to situations like VI.4? What obstacles do incommensurable magnitudes pose in the construction of a real number system?
Proportionality in Similar Triangles: A Cross-Cultural Comparison - Conclusion
While the ratio of corresponding sides in similar triangles may be equal, and this equality is often justified by an appeal to reason, such an appeal relies on the Euclidean parallel postulate. Many scholars in the 2000 years following Euclid have attempted to prove the parallel postulate, and in doing so, unsuspectingly clarified for modern mathematics exactly what theorems or constructions are equivalent to this axiom of parallels. John Wallis (1616-1703) "proved" the parallel postulate beginning from a statement about the existence of similar triangles with proportional sides. Both Girolamo Saccheri (1667-1733) and Johann Heinrich Lambert (1728-1777) sought inherent contradictions in hyperbolic geometry by studying the implications of "rectangles" with angle sum less than 360° [2 ]. Today the work of these two geometers can be interpreted as demonstrating that in non-Euclidean geometry, there are no rectangles, squares, nor a true "square unit" of measure.
In the non-Euclidean case, part 4(a) above would fail, since it cannot be the case that line AJ and FL when extended meet in a right angle and lines AB, FE also meet in a right angle. Moreover, in hyperbolic geometry, the angle sum of a triangle is less than 180°, with larger triangles having a smaller angle sum. In spherical geometry, a triangle has angle sum greater than 180°, with larger triangles having greater angle sum. In non-Euclidean geometry, if two triangles have all three corresponding angles equal, the triangles are in fact congruent [2, p. 190]. In this sense, the property of similarity is more restrictive in the non-Euclidean world. In teaching the module, the instructor should identify where in the proof of Euclidean similarity theorems the concept of area occurs, and, if time permits, explain that the construction of a rectangle depends on the Euclidean parallel postulate. This could be used as a spring board to study hyperbolic geometry or to motivate attempts to prove the parallel postulate, since many appealing theorems fail without this axiom. For further results in other geometries, see Euclidean and Non-Euclidean Geometries [2 ], or the chapter on the parallel postulate in Mathematical Expeditions [6].
The instructor may assign all parts (a)-(e) as a one-week individual or group project, or simply assign the parts one-by-one as in-class problems or out-of-class exercises. Also, part (e) may be omitted if the Pythagorean Theorem has already been covered, or part (e) may be assigned independently of the other parts.
Acknowledgment: The work for this article has been partially supported by the National Science Foundation's Course, Curriculum and Laboratory Improvement Program under grant DUE-0717752, for which the author is most appreciative. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation.
Proportionality in Similar Triangles: A Cross-Cultural Comparison - References
- 1. Heath, T.L. (editor), The Thirteen Books of Euclid's Elements, Vols. I, II, Dover Inc., New York, 1956.
2. Greenberg, M.J., Euclidean and Non-Euclidean Geometries: Development and History, third edition, Freeman and Company, New York, 1993.
- 3. Hollingdale, S., Makers of Mathematics, Penguin Books, London, 1994.
4. Katz, V., A History of Mathematics: An Introduction, second edition, Addison Wesley, New York, 1998.
- 5. Katz, V. (editor), The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook, Princeton University Press, Princeton, New Jersey, 2007.
6. Laubenbacher, R., Pengelley, D., Mathematical Expeditions: Chronicles by the Explorers, Springer Verlag, New York, 2000.
- 7. Swetz, F.J., The Sea Island Mathematical Manual: Surveying and Mathematics in Ancient China, The Pennsylvania State University Press, University Park, Pennsylvania, 1992.
8. Yan, L., Shiran, D., Chinese Mathematics: A Concise History, Crossley, J.N., Lun A. (translators), Clarendon Press, Oxford, 1987.