Mathematical Treasures - Jan de Witt's Elements of Curves

This is the title page of the Elements of Linear Curves by Jan de Witt (1625 - 1672). De Witt was a student of Frans van Schooten, who published this work in his 1661 edition of Descartes' Geometry. (This copy is from the 1683 edition. And, in fact, de Witt himself probably finished the work by 1646.) The first of the two books of this treatise was devoted to developing the properties of the conic sections using synthetic methods based on the work of Apollonius. But in the second book, de Witt produced a complete algebraic treatment of the conics, beginning with equations in two variables, based on the work of Fermat and Descartes.
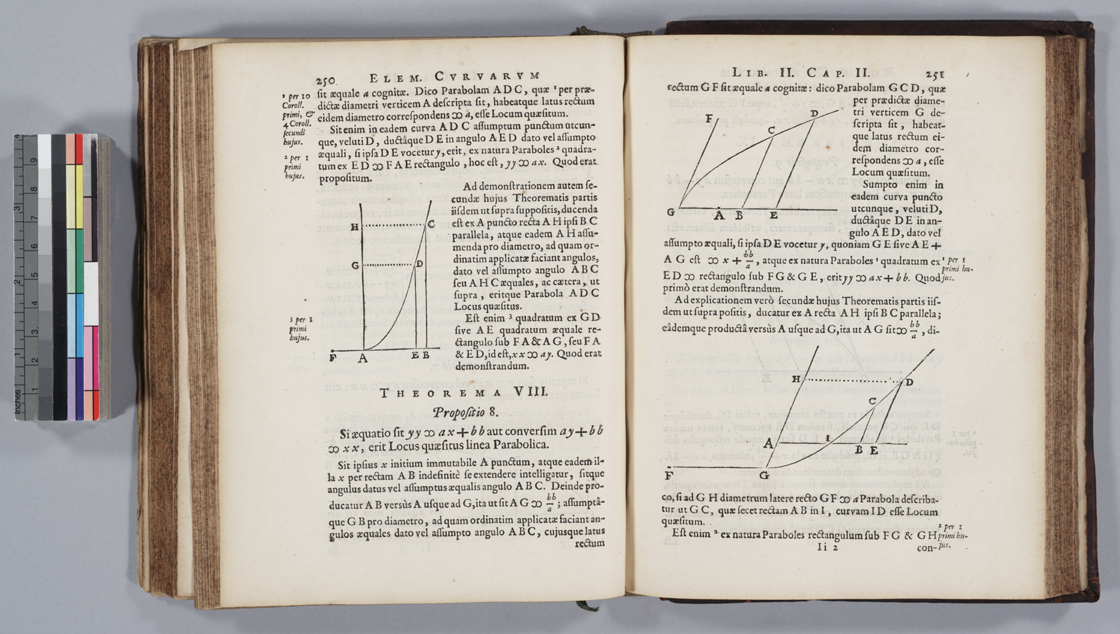
On pages 250-251, de Witt shows that the equations yy = ax + bb and xx = ay + bb determine parabolas. The proof is based on the "nature of a parabola." Note that de Witt still uses Descartes' symbol for "=" as well as his homogeneity rules in making sure that each side of the equation is two-dimensional. Note also that the diagrams show that de Witt did not stick to perpendicular axes and that he only considered what we would call the first quadrant. That is, all of the values displayed were positive.

Here, on p. 263, de Witt shows how to rotate the axes to turn a complicated second degree equation in two variables into the standard one displayed earlier. Unlike in modern treatises, de Witt does not use trigonometry, but gives the equations of the new axes in terms of the old ones. That is, he uses a transformation of coordinates based on the form of the given equation.

On pp. 276-277, de Witt shows that certain equations in two variables determine a hyperbola, in particular, the equation lyy/g = xx - ff and its analog with the variables reversed. Again, his proof requires the "nature of a hyperbola", and, of course, this "nature" comes from de Witt's understanding of the work of Apollonius.

On p. 283, de Witt shows how to make the appropriate transformation of coordinates to change a complicated quadratic function of two variables into the recognizable form of a hyperbola. As before, he does not use trigonometry.