Students often encounter formulas for sums of powers of the first n positive integers as examples of statements that can be proved using the Principle of Mathematical Induction and, perhaps less often nowadays, in Riemann sums during an introduction to definite integration. In either situation, they usually see only the first three such sum formulas,

$$1 + 2 + 3 + \cdots + n = {{n(n + 1)}\over 2}$$

$$1^2 + 2^2 + 3^2 + \cdots + n^2 = {{n(n + 1)(2n + 1)} \over 6}$$

and

$$1^3 + 2^3 + 3^3 + \cdots + n^3 = {{n^2 (n + 1)^2 } \over 4}$$

for any positive integer n.

Formulas for sums of integer powers were first given in generalizable form in the West by Thomas Harriot (c. 1560-1621) of England. At about the same time, Johann Faulhaber (1580-1635) of Germany gave formulas for these sums up to the 17^th power, far higher than anyone before him, but he did not make clear how to generalize them. Pierre de Fermat (1601-1665) often is credited with the discovery of formulas for sums of integer powers, but his fellow French mathematician Blaise Pascal (1623-1662) gave the formulas much more explicitly. The Swiss mathematician Jakob Bernoulli (1654-1705) is perhaps best and most deservedly known for presenting formulas for sums of integer powers to the European mathematical community. His was the most useful and generalizable formulation to date because he gave by far the most explicit and succinct instructions for finding the coefficients of the formulas.

In this article, we first recount some of the early history of formulas for sums of integer powers. We then explore how each of the mathematicians listed above developed, understood, and presented their formulas. Along the way, we shall see that the phrase “general formula” is relative terminology: during the late sixteenth and early seventeenth centuries mathematicians were just beginning to replace verbal descriptions by symbolic representations and we may be surprised to discover that some mathematicians’ “formulas” were given entirely in words and/or were given just for the first few exponents with the remaining cases covered by “et cetera”. At the end of each section, we present exercises and activities designed to help students develop a deeper understanding of the ideas and methods of each of the mathematicians we discuss.

The Greek mathematician, philosopher, and mystic Pythagoras is said to have lived with his followers, the Pythagoreans, at Croton in what is now southern Italy. The Pythagoreans took as their motto “All is Number” and were believed to have experimented with number properties by arranging pebbles on a flat surface. As a result, they saw what we would describe as a sum of successive positive integers as a triangle or triangular number (Fig. 1).

 

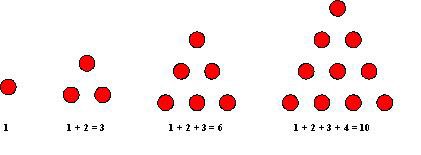
Figure 1. The first four triangular numbers

 

Their pebble experiments led them to see that two copies of the same triangular number could be fitted together to form an oblong number; hence, for example, twice the triangular number 15 = 1 + 2 + 3 + 4 + 5 could be viewed as the oblong number 5 x 6 = 30 (Fig. 2).

 

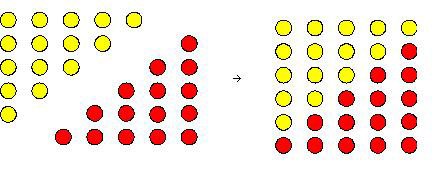
Figure 2. Twice a triangular number is an oblong number, or, in modern notation, \(2(1 + 2 + 3 + \cdots + n) = n(n + 1).\) Here we see that \(2(1 + 2 + 3 + 4 + 5) = 5\cdot 6.\)

 

Equivalently, any triangular number was half an oblong number; for example,

$$1 + 2 + 3 + 4 + 5 = {{5 \cdot 6} \over 2},$$

and, in general,

$$1 + 2 + 3 + \cdots + n = {{n(n + 1)} \over 2}$$

for any positive integer n.

 

Exercise 1: Use pebbles to illustrate that the sum of every two consecutive triangular numbers is a square number. Hint: Examples of pairs of consecutive triangular numbers include 6 and 10, 10 and 15, and 15 and 21.

 

The solution to this exercise is available here.

The Greek mathematician, scientist, and inventor Archimedes spent most of his life in Syracuse in southern Italy. Considered the greatest mathematician of antiquity, he is famous for a number of mathematical and scientific discoveries and also for a number of inventions, many of them machines of war used in his city’s defense against Roman armies. Archimedes knew the Pythagorean “formula” for the sum of the first n positive integers. He almost certainly knew also a “formula” for the sum of the squares of the first n positive integers. His Lemma to Proposition 2 in On Conoids and Spheroids (Heath, p. 57) and his Proposition 10 in On Spirals (Heath, pp. 68-69), translated to our symbols, say that

$$(n + 1)n^2 + (1 + 2 + 3 + \cdots + n) = 3(1^2 + 2^2 + 3^2 + \cdots + n^2 )\quad (*),$$

as illustrated in Figure 3 (see also Nelsen, p. 77, and Stein, pp. 46-49).

 

Figure 3 shows literally that

$$3(1^2 + 2^2 + 3^2 + 4^2 ) = 5 \cdot 4^2 + (1 + 2 + 3 + 4).$$

Using the Pythagorean formula to replace \(1 + 2 + 3 + · · · ­+ n\) by \({{n(n + 1)} \over 2}\) in Archimedes' equation

$$(n + 1)n^2 + (1 + 2 + 3 + \cdots + n) = 3(1^2 + 2^2 + 3^2 + \cdots + n^2 )\quad (*),$$

we have

$$(n + 1)n^2 + {\frac{n(n + 1)}{2}} = 3(1^2 + 2^2 + 3^2 + \cdots + n^2 ).$$

Solving for the sum of squares, we get

$$1^2 + 2^2 + 3^2 + \cdots + n^2 = {\frac{(n + 1)n^2}{3}} + {\frac{n(n + 1)}{6}},$$

or $$1^2 + 2^2 + 3^2 + \cdots + n^2 = {{n(n + 1)(2n + 1)} \over 6}$$

for all positive integers n.

 

Since Archimedes concluded in a Corollary to his Lemma to Proposition 2 (Heath, p. 57) that

$$3(1^2 + 2^2 + 3^2 + \cdots + n^2 ) > n^3 > 3(1^2 + 2^2 + 3^2 + \cdots + (n - 1)^2 ),$$

presumably, he, too, replaced \(1 + 2 + 3 + · · · ­+ n\) by \({{n(n + 1)} \over 2}\) in his equation (*), and deduced that

$$1^2 + 2^2 + 3^2 + \cdots + n^2 = {{n(n + 1)(2n + 1)} \over 6}.$$

Again, Archimedes would have described these equations and inequalities in words rather than symbols.

 

Exercise 2: Use cubes (or squares) to represent the triangular numbers and to illustrate the identity

$$1 + 2 + 3 + \cdots + n = {{n(n + 1)} \over 2}$$

and the identity from Exercise 1.

 

Exercise 3: Use 60 or 120 cubes to illustrate the identity

$$1 + 3 + 6 + \cdots + {{n(n + 1)} \over 2} = {{n(n + 1)(n + 2)} \over 6}$$

for n = 3 or n = 4. Hint: One way to construct a pyramid representing the sum of the first four triangular numbers, 1, 3, 6, and 10, is to place a single cube representing 1 atop a configuration of three cubes, which, in turn, is placed atop a configuration of 6 cubes, as shown in Figure 4. Just one more layer of 10 cubes will result in a pyramid containing 1 + 3 + 6 + 10 cubes. How many such pyramids should you construct in order to form a 4-cube by 5-cube by 6-cube rectangular solid? (Nelsen, p. 95)

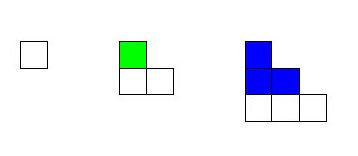
Figure 4. Place the single cube atop the shaded portion of the layer of three cubes. Place the resulting pyramid of 1 + 3 cubes atop the shaded portion of the layer of six cubes. Only tops of cubes are shown.

 

Solutions to these exercises can be found here.

The northern Indian mathematician and astronomer, Aryabhata, born in 476, wrote one of the earliest known Indian mathematics and astronomy books, the Aryabhatiya, in 499 (Katz, p. 212). In Section II, Stanza 22, of the Aryabhatiya, he wrote:

The sixth part of the product of three quantities consisting of the number of terms, the number of terms plus one, and twice the number of terms plus one is the sum of the squares. The square of the sum of the (original) series is the sum of the cubes. (Katz, 217)

The first sentence gives the formula from pages 1 and 3, above, for the sum of the squares; the second says, in our notation, that

$$(1 + 2 + 3 + \cdots + n)^2 = 1^3 + 2^3 + 3^3 + \cdots + n^3.$$

If we replace \(1 + 2 + 3 + · · · ­+ n\) by \({{n(n + 1)} \over 2}\), we obtain

$$1^3 + 2^3 + 3^3 + \cdots + n^3 = \left( {{{n(n + 1)} \over 2}} \right)^2.$$

It seems likely that mathematicians discovered this formula for the sum of the cubes early on by taking note of examples, such as

$$1^3 = 1 = 1^2, $$

$$1^3 + 2^3 = 9 = 3^2 = (1 + 2)^2,$$

$$1^3 + 2^3 + 3^3 = 36 = 6^2 = (1 + 2 + 3)^2, $$ and

$$1^3 + 2^3 + 3^3 + 4^3 = 100 = 10^2 = (1 + 2 + 3 + 4)^2. $$

We would then generalize to

$$1^3 + 2^3 + 3^3 + \cdots + n^3 = (1 + 2 + 3 + \cdots + n)^2 $$

and hence to

$$1^3 + 2^3 + 3^3 + \cdots + n^3 = \left( {{{n(n + 1)} \over 2}} \right)^2.$$

for all positive integers n.

Exercise 4: Use 84 or 180 cubes to demonstrate the identity $$1^2 + 2^2 + 3^2 + \cdots + n^2 = {{n(n + 1)(2n + 1)} \over 6}$$

for n = 3 or n = 4, as described by the Indian mathematician Nilakantha (c. 1445-1545). A member of the famous Kerala school of mathematics and astronomy in southern India, Nilakantha wrote a commentary on the Aryabhatiya in which he gave the following proof of the identity above. He explained that six copies of the sum $$1^2 + 2^2 + 3^2 + \cdots + n^2$$

form an n by (n + 1) by (2n + 1) rectangular solid as follows. Start on the outside with a floor and three walls consisting of 6n² cubes, then work from the outside inwards, lining the inside of the existing shell with a floor and three walls consisting of 6(n – 1)² cubes, then 6(n – 2)² cubes, . . . , then 6 • 2² cubes, and finally 6 • 1² cubes. The outside shell has height n, depth n + 1, and length 2n + 1, with one long side open and the top open. If n = 3, this shell has dimensions 3, 4, and 7, and consists of 6 • 3² = 54 cubes. Construct this shell, then, inside of it, a shell having dimensions 2, 3, and 5 and consisting of 6 • 2² = 24 cubes, and then, inside of the double shell, a 1 x 2 x 3 layer consisting of 6 • 1² = 6 cubes. The result should be a 3 x 4 x 7 rectangular solid. This construction illustrates that

$$6 \cdot 1^2 + 6 \cdot 2^2 + 6 \cdot 3^2 = 3 \cdot 4 \cdot 7 \quad {\rm or} \quad 1^2 + 2^2 + 3^2 = {{3 \cdot 4 \cdot 7} \over 6},$$

or, more generally, $$1^2 + 2^2 + 3^2 + \cdots + n^2 = {{n(n + 1)(2n + 1)} \over 6}$$

for any positive integer n.

That the outside shell contains 6n² cubes can be seen by noting that the shell can be built using an n x 2n slab for the floor, another n x 2n slab for the back wall, and n x (n - 1) and n x (n + 1) slabs for the side walls. Remember that the outside shell has height n, depth n + 1, and length 2n + 1, with one long side open and the top open, and that all inside shells should be constructed with dimensions like those of the outside shell.

(See Katz, Victor, 2009, A History of Mathematics: An Introduction (3^rd ed.), Boston: Addison-Wesley, pp. 251-252, or Katz, Victor (editor), 2007, The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook, Princeton University Press, pp. 493-496.)

Exercise 5: Use 60 or 120 cubes to illustrate the identity $$1 + 3 + 6 + \cdots + {{n(n + 1)} \over 2} = {{n(n + 1)(n + 2)} \over 6}$$

for n = 3 or n = 4, as Nilakantha may have done. Our strategy will be to demonstrate that six copies of the sum $$1 + 3 + 6 + \cdots + {{n(n + 1)} \over 2}$$ form an n by (n + 1) by (n + 2) rectangular solid, as follows. Start on the outside with an (n + 1) by (n + 2) floor and two adjoining walls of height n, consisting of \(6 \cdot \frac{n(n+1)}{2} \) cubes all together, then work from the outside inwards, lining the inside of the existing shell with a floor and two adjoining walls consisting of \(6\cdot \frac{(n-1)n}{2} \) cubes, . . . , 6 • 3 cubes, and finally 6 • 1 cubes. For n = 3, the 3 x 4 x 5 outside shell consists of \(6\cdot \frac{3\cdot4}{2} = 36\) cubes, the 2 x 3 x 4 shell inside of this one \(6 \cdot {\frac{2\cdot3}{2}} = 18\) cubes, and the 1 x 2 x 3 inner shell or layer \(6\cdot \frac{1\cdot2}{2} = 6\) cubes. This construction illustrates that

$$6 (1 + 3 + 6) = {{3\cdot 4\cdot 5}}$$

or

$$1 + 3 + 6 = {{3\cdot 4\cdot 5} \over 6}$$

or, more generally,

$$1 + 3 + 6 + \cdots + {{n(n + 1)} \over 2} = {{n(n + 1)(n + 2)} \over 6}$$

for any integer n.

That the outside shell contains \(6\cdot\frac{n(n+1)}{2}=3n(n+1)\) cubes can be seen by noting that the shell can be built using an n x (n + 1) slab for the floor and two adjoining wall slabs with dimensions n x n and n x (n + 2). This will result in an outside shell with height n, length n + 1, and width n + 2. The inside shells should be constructed with dimensions like those of the outside shell.

(See Joseph, George Gheverghese, 2000, The Crest of the Peacock, Princeton University Press, pp. 295-296, and the references given for Exercise 4.)

Exercise 6: How might early mathematicians have discovered the identity from Exercise 1? Provide at least four examples and write the identity in terms of n, where n is a positive integer.

For solutions to these exercises, click here.

The mathematician Abu Bakr Al-Karaji worked in Baghdad in what is now Iraq for at least part, if not all, of his life. He wrote books on engineering and mathematics, most notably algebra, and died in 1019 (Katz, p. 251).

Al-Karaji stated the result on the sum of the cubes for n = 10 as (using our notation) $$1^3 + 2^3 + 3^3 + \cdots + 10^3 = (1 + 2 + 3 + \cdots + 10)^2, $$

and proved it as follows (Katz, p. 255): If the square shown in Figure 5 has side length 1 + 2 + 3 + · · · + 10, then the square has area (1 + 2 + 3 + · · · + 10)².

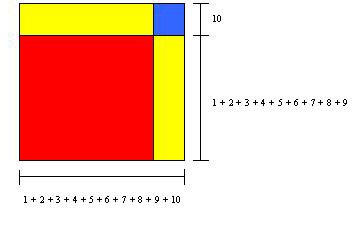
Figure 5. The area of this square can be written in (at least) two different ways.

Likewise, the red square with side length 1 + 2 + 3 + · · · + 9 has area (1 + 2 + 3 + · · · + 9)². Since each yellow rectangle has area 10(1 + 2 + 3 + · · · + 9) and the blue square has area 10², then the gnomon consisting of the two yellow rectangles and the blue square in Figure 5 has area $$2 \cdot 10(1 + 2 + 3 + \cdots + 9) + 10^2 = 2 \cdot 10 \cdot {{9 \cdot 10} \over 2} + 10^2 = 10 \cdot 10^2 = 10^3. $$

This gives us another way to write the area of the larger square; namely, as the sum of the areas of the red square and of the gnomon, or (1 + 2 + 3 + · · · + 9)² + 10³. Equating our two expressions for the area of the larger square, we have

$$(1 + 2 + 3 + \cdots + 9)^2 + 10^3 =(1 + 2 + 3 + \cdots + 10)^2.$$

Repeating the preceding argument for the square with side length 1 + 2 + 3 + · · · + 9 and a smaller square with side length 1 + 2 + 3 + · · · + 8, we have

$$(1 + 2 + 3 + \cdots + 8)^2 + 9^3 =(1 + 2 + 3 + \cdots + 9)^2.$$

Substituting in the preceding equation, we get

$$(1 + 2 + 3 + \cdots + 8)^2 + 9^3 + 10^3 =(1 + 2 + 3 + \cdots + 10)^2.$$

After repeating the argument seven more times, we obtain

$$1^3 + 2^3 + 3^3 + \cdots + 10^3 = (1 + 2 + 3 + \cdots + 10)^2,$$

al-Karaji’s result.

The mathematican, astronomer, and Biblical scholar Levi ben Gerson (1288-1344), who lived in southern France, gave a similar proof that (1 + 2 + 3 + · · · + n)² = 1³ + 2³ + 3³ + · · · + n³, which he stated as Proposition 42 in his Maasei Hoshev (The Art of the Calculator), as follows (Katz, pp. 302-304).

The square of the sum of the natural numbers from 1 up to a given number is equal to the sum of the cubes of the numbers from 1 up to the given number. (Katz, p. 304)

The connection given in this formula between sums of cubes and sums of integers might give us hope that the sum of the fourth powers also could be expressed very simply in terms of the sum of integers and/or the sum of squares. Unfortunately, the pattern is not at all transparent, even after writing the formulas for the three sums we’ve considered so far in polynomial form, as follows:

$$1 + 2 + 3 + \cdots + n = {{n^2 } \over 2} + {n \over 2},$$

$$1^2 + 2^2 + 3^2 + \cdots + n^2 = {{n^3 } \over 3} + {{n^2 } \over 2} + {n \over 6},$$

and

$$1^3 + 2^3 + 3^3 + \cdots + n^3 = {{n^4 } \over 4} + {{n^3 } \over 2} + {{n^2 } \over 4}.$$

We can predict that a polynomial formula for

$$1^k + 2^k + 3^k + \cdots + n^k, $$

for k a positive integer, would begin

$${{n^{k + 1} } \over {k + 1}} + {{n^k } \over 2} + \cdots,$$

and, by substituting n = 1 into each side of the equation, we can see that the sum of the coefficients of the polynomial would be 1.

Exercise 7: For n = 4 (rather than n = 10), work through al-Karaji’s argument that (1 + 2 + 3 + 4)² = 1³ + 2³ + 3³ + 4³ in three steps, illustrating each step using the same large square. The left side of the equation is the height times the width of this large square, hence is its area. Which regions of the large square does the right side of the equation represent? That is, of which region of the large square does each of the four terms in the right side of the equation give the area? Hint: Gnomons!

Exercise 8: According to the last sentence of the section, what are the possible polynomial formulas for the sum of the fourth powers, 1⁴ + 2⁴ + 3⁴ + · · · + n⁴? List three possibilities.

For solutions to these exercises, click here.

The mathematician and scientist Abu Ali al-Hasan ibn al-Hasan ibn al-Haytham (965-1039) was born in Basra in what is now southern Iraq, but spent most of his working life in Egypt.  He is most famous for his book Optics and specifically for the reflection problem named after him, “Alhazen’s Problem” (Katz, p. 256).

For his volume computations, al-Haytham needed formulas for the sums of the first n integer cubes and the first n fourth powers (C.H. Edwards, p. 83).  He may have used a diagram like that in Figure 6 (Baron, p. 70) to describe the relationship \[(4 + 1)\sum_{i = 1}^4 i  = \sum_{i = 1}^4 {i^2 }  + \sum_{p = 1}^4 {\sum_{i = 1}^p i }.\]

 

Figure 6.  The area of this rectangle can be written in (at least) two different ways (after Baron, p. 70).

 

The area of the rectangle in Figure 6 can be written in (at least) two different ways.  Length times width gives area \[(4 + 1)(1 + 2 + 3 + 4),\] whereas adding together the areas of the eight regions gives area \[(1^2 + 2^2 + 3^2 + 4^2) + (1 + (1 + 2) + (1 + 2 + 3) + (1 + 2 + 3 + 4)).\]

Since each of these two expressions equals the area of the same rectangle, the two expressions are equal to one another.  Writing them using summation notation, we obtain the equation \[(4 + 1)\sum_{i = 1}^4 i  = \sum_{i = 1}^4 {i^2 }  + \sum_{p = 1}^4 {\sum_{i = 1}^p i },\]

which can be solved for \[\sum_{i = 1}^4 {i^2 },\]

the sum of the first four squares.  Replacing 4 by n, we have the equation \[(n + 1)\sum_{i = 1}^n i  = \sum_{i = 1}^n {i^2 }  + \sum_{p = 1}^n {\sum_{i = 1}^p i },\]

which can be solved for \[\sum_{i = 1}^n {i^2 },\]

the sum of the first n squares.

The diagram in Figure 7 illustrates the more general relationship \[(n + 1)\sum_{i = 1}^n {i^k  = } \sum_{i = 1}^n {i^{k + 1} }  + \sum_{p = 1}^n {\sum_{i = 1}^p {i^k } },\]

where each side of the equation gives the area of the rectangle (C.H. Edwards, p. 84). 

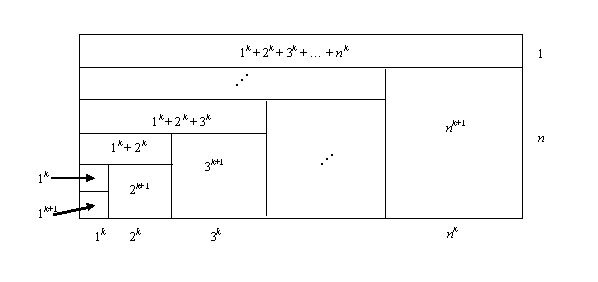
Figure 7.  The area of the rectangle in this figure, a generalization of Figure 6, can be written in (at least) two different ways (after C.H. Edwards, p. 84).

 

If we let k = 1 (see the preceding paragraph and Exercise 10) and use the formula \[1 + 2 + 3 +  \cdots  + n = {{n(n + 1)} \over 2},\]

we obtain \[1^2  + 2^2  + 3^2  +  \cdots  + n^2  = {{n(n + 1)(2n + 1)} \over 6}.\]

If we let k = 2 and substitute, using the formula for the sum of the squares, we obtain \[1^3  + 2^3  + 3^3  +  \cdots  + n^3  = \left( {{{n(n + 1)} \over 2}} \right)^2\]

(see Exercise 11).  If we let k = 3, we obtain \[(n + 1)\sum_{i = 1}^n i^3  =  \sum_{i = 1}^n {i^4 }  + \sum_{p = 1}^n {\sum_{i = 1}^p {i^3 } },\]

or

\(\displaystyle{(n+1)(1^3  + 2^3  + 3^3  +  \cdots  + n^3 ) =}\)

\[(1^4  + 2^4  + 3^4  +  \cdots  + n^4 ) + \sum\limits_{p = 1}^n {(1^3  + 2^3  + 3^3  +  \cdots  + p^3 )};\]

or

\(\displaystyle{1^4  + 2^4  + 3^4  +  \cdots  + n^4  =}\) \[(n + 1)(1^3  + 2^3  + 3^3  +  \cdots  + n^3 ) - \sum_{p = 1}^n {(1^3  + 2^3  + 3^3  +  \cdots  + p^3 )}\]

If we now apply the formula for the sum of the cubes, the equation becomes \[1^4  + 2^4  + 3^4  +  \cdots  + n^4  = (n + 1)\left( {{{n(n + 1)} \over 2}} \right)^2  - \sum_{p = 1}^n {\left( {{{p(p + 1)} \over 2}} \right)^2 }\]

\[ = (n + 1)\left( {{{n^4 } \over 4} + {{n^3 } \over 2} + {{n^2 } \over 4}} \right) - \sum_{p = 1}^n {\left( {{{p^4 } \over 4} + {{p^3 } \over 2} + {{p^2 } \over 4}} \right)} \]

\[ = {{n^5 } \over 4} + {{3n^4 } \over 4} + {{3n^3 } \over 4} + {{n^2 } \over 4} - {1 \over 4}\sum_{p = 1}^n {p^4 }  - {1 \over 2}\sum_{p = 1}^n {p^3 }  - {1 \over 4}\sum_{p = 1}^n {p^2 } \]

\[ = {{n^5 } \over 4} + {{3n^4 } \over 4} + {{3n^3 } \over 4} + {{n^2 } \over 4} - {1 \over 4}\left( {1^4  + 2^4  +  \cdots  + n^4 } \right) - {1 \over 2}\left( {1^3  + 2^3  +  \cdots  + n^3 } \right)\]

\(\displaystyle{{-\frac{1}{4}}\left(1^2 + 2^2  +  \cdots + n^2 \right).}\)

Collecting sums of fourth powers and applying the formulas for sums of cubes and squares, we have

\[{5 \over 4}\left( {1^4  + 2^4  +  \cdots  + n^4 } \right) = {{n^5 } \over 4} + {{3n^4 } \over 4} + {{3n^3 } \over 4} + {{n^2 } \over 4} - {1 \over 2}\left( {{{n^4 } \over 4} + {{n^3 } \over 2} + {{n^2 } \over 4}} \right)\]

\(\displaystyle{{-\frac{1}{4}}\left({\frac{n(n+1)(2n+1)}{6}} \right)}\)

or \[1^4  + 2^4  +  \cdots  + n^4  = {{n^5 } \over 5} + {{n^4 } \over 2} + {{n^3 } \over 3} - {n \over {30}}\]

for all positive integers n.  Al-Haytham actually used n = 4 in his work, then stated the general result in words (Katz, pp. 256-257).  Translating al-Haytham’s words into our symbols, we have (Katz, p. 258) \[1^4  + 2^4  + 3^4  +  \cdots  + n^4  = \left( {{n \over 5} + {1 \over 5}} \right)n\left( {n + {1 \over 2}} \right)\left( {(n + 1)n - {1 \over 3}} \right)\]

for all positive integers n.
 

The righthand side of this equation is a multiple of \[{{n(n + 1)(2n + 1)} \over 6},\]

the sum of the first n positive integer squares, hence also of \[{{n(n + 1)} \over 2},\]

the sum of the first n positive integers.

 

Exercise 9:  Draw a rectangular figure like Figure 6 that illustrates the identity \[(4 + 1)\sum\limits_{i = 1}^4 {i^2 }  = \sum_{i = 1}^4 {i^3 }  + \sum_{p = 1}^4 {\sum_{i = 1}^p {i^2 } }.\]

Your rectangle will have height 5 and width 30.  Your figure need not be drawn to scale!

 

Exercise 10:  Draw a rectangular figure like Figure 6 or 7 that illustrates the identity \[(n + 1)\sum_{i = 1}^n {i = } \sum_{i = 1}^n {i^2 }  + \sum_{p = 1}^n {\sum_{i = 1}^p i }.\]

Provide the details of the computation that shows that letting k = 1 in the equation \[(n + 1)\sum_{i = 1}^n {i^k  = } \sum_{i = 1}^n {i^{k + 1} }  + \sum_{p = 1}^n {\sum_{i = 1}^p {i^k } }\]

leads to the formula \[1^2  + 2^2  + 3^2  +  \cdots  + n^2  = {{n(n + 1)(2n + 1)} \over 6}.\]

 

Exercise 11:  Draw a rectangular figure like Figure 7 that illustrates the identity \[(n + 1)\sum_{i = 1}^n {i^2  = } \sum_{i = 1}^n {i^3 }  + \sum_{p = 1}^n {\sum_{i = 1}^p {i^2 }}.\]

Provide the details of the computation that shows that letting k = 2 in the equation \[(n + 1)\sum_{i = 1}^n {i^k  = } \sum_{i = 1}^n {i^{k + 1} }  + \sum_{p = 1}^n {\sum_{i = 1}^p {i^k }}\]

leads to the formula \[1^3  + 2^3  + 3^3  +  \cdots  + n^3  = \left( {{{n(n + 1)} \over 2}} \right)^2.\]

 

Exercise 12:  Show how to write al-Haytham’s formula \[\left( {{n \over 5} + {1 \over 5}} \right)n\left( {n + {1 \over 2}} \right)\left( {(n + 1)n - {1 \over 3}} \right)\]

for the sum of the first n fourth powers as a rational multiple of \[{{n(n + 1)(2n + 1)} \over 6}.\]

 

Solutions to these exercises can be found by clicking here.

Thomas Harriot was an English mathematician and scientist who lived in London and worked under the patronage of Sir Walter Raleigh and Henry Percy, Earl of Northumberland.  Raleigh sent Harriot on a voyage to the Virginia Colony in 1585-1586, allowing Harriot to put his navigational theory into practice and also to gather extensive notes for his book, A Briefe and True Report of the New Found Land of Virginia, first published in 1588.

Harriot never published any of his mathematical or scientific work, but he left over 5000 manuscript sheets of notes on various topics.  In his notes on mathematics, he made much greater use of symbolic notation than his contemporaries and many of his successors, including Fermat and Pascal (see below).  He also made frequent use of difference tables, employing them to study Pythagorean triples and, as we shall see, sums of powers of positive integers.

Harriot wrote formulas for sums of squares, cubes, and fourth powers on a manuscript sheet headed “Ad aggregata Z. C. ZZ. et c.” (“For sums of squares, cubes, square-squares, etc.”) (Harriot, folio 240).  In this heading, we have substituted Z, C, and ZZ for symbols for squares, cubes, and fourth powers (square-squares) that Harriot probably borrowed from Robert Recorde’s famous algebra book, Whetstone of Witte (1557), and we have substituted “et c.” for the symbol Harriot used for “et cetera”. 

Figure 8.  Robert Recorde's cossist notation for powers can be seen in the list beginning at lower left and ending in the middle of the righthand page, along with simplified versions written in by a reader.  The symbols R for the "roote" (first power), Z for the "square," C for the "cubike" (cube), and ZZ for the "square of squares" (fourth power) are at left.  For additional images from Recorde's algebra book, The Whetstone of Witte, see Robert Recorde's Whetstone of Witte in "Mathematical Treasures." (Reproduced by permission of Columbia University Library)

 

On the preceding manuscript sheet, Harriot wrote three difference tables, one containing a column of squares, another a column of cubes, and a third a column of square-squares (Harriot, f. 239), as shown in Figure 9.

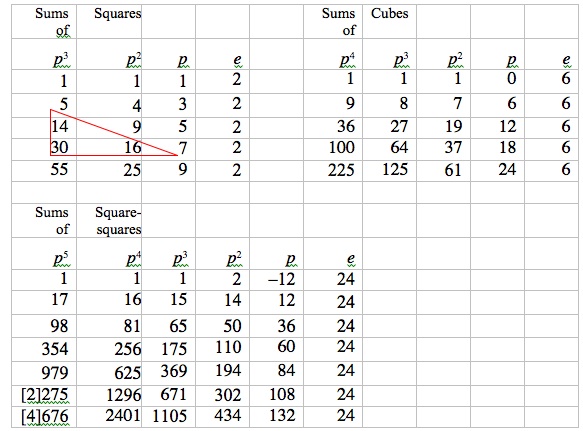
Figure 9. Difference tables for sums of squares, cubes, and square-squares

 

These tables are called “difference” tables because, for instance, in the triangle of numbers

$$\matrix{ 14 & {}\cr 30 & 16\cr}$$

in the upper lefthand table in Figure 9, the difference between 30 and 14 is 16 (30 – 14 = 16).  This difference relationship holds for every such triangle of numbers in the tables in Figure 9 and characterizes these tables as difference tables.  If we apply this difference property repeatedly, we see that entries of any column may be summed to obtain entries of the column just to the left.  For example, in the two leftmost columns of the upper lefthand table in Figure 9, we see that 14 + 16 + 25 = 55, 5 + 9 + 16 + 25 = 55, 1 + 4 + 9 + 16 + 25 = 55, and 1 + 4 + 9 + 16 = 30.  These last two sums are, respectively, the sum of the first five positive integer squares and the sum of the first four positive integer squares, and it follows directly from the definition of difference table and Harriot’s selection of 1 as the first entry of the column labeled p³ and the consecutive positive integer squares as the entries of the column labeled p² that the nth number in the column labeled p³  is the sum of the first n positive integer squares.  (Note that 2 and 3 are superscripts here, rather than exponents.)  Likewise, in Harriot’s remaining two difference tables, since the second columns of the tables contain the cubes and fourth powers of successive positive integers, then the first or leftmost columns contain, respectively, the sums of cubes and the sums of fourth powers of successive positive integers. 

These difference tables are in fact called “constant” difference tables because the differences become constant in the column labeled “e”.  Harriot had general formulas for the entries of constant difference tables and could apply these formulas to the leftmost columns of his tables in Figure 9 to obtain general formulas for sums of squares, cubes, and fourth powers of successive positive integers.  Harriot’s formulas, given in terms of the first row of entries in a constant difference table, were as follows (Harriot, ff. 234, 246).

$$\eqalign{&1 v^1  = en - e  \cr &\quad \quad \quad  + p \cr} $$

$$\eqalign{& 2 v^2 = enn - en \cr & \quad \quad \quad \quad + 2pn - 2p \cr & \quad \quad \quad \quad \quad \quad \; + 2 p^2 \cr}$$

$$\eqalign{  & 6 v^3  = ennn - 0enn - en  \cr   & \quad \quad \quad \quad  + 3pnn - 3pn  \cr   & \quad \quad \quad \quad \quad \quad \quad  + 6 p^2 n - 6 p^2   \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad  + 6 p^3  \cr} $$

$$\eqalign{  & 24 v^4  = ennnn + 2ennn - enn - 2en  \cr   & \quad \quad \quad \quad \quad  + 4pnnn - 0pnn - 4pn  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad  + 12 p^2 nn - 12 p^2 n  \cr  & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad  + 24 p^3 n - 24 p^3   \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \; + 24 p^4  \cr} $$

$$\eqalign{  & 120 v^5  = ennnnn + 5ennnn + 5ennn - 5enn - 6en  \cr   & \quad \quad \quad \quad \quad \quad  + 5pnnnn + 10pnnn - 5pnn - 10pn  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad  + 20 p^2 nnn - 0 p^2 nn - 20 p^2 n  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad  + 60 p^3 nn - 60 p^3 n  \cr  & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \; + 120 p^4 n - 120 p^4   \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \;\quad \quad \quad \quad  + 120 p^5  \cr} $$

Here, v¹ gives the nth entry of the column labeled p, v² the nth entry of the column labeled p² , v³ the nth entry of the column labeled p³ , v⁴ the nth entry of the column labeled p⁴, and v⁵ the nth entry of the column labeled p⁵.  For the upper left table in Figure 9, the formula for v³ with e = 2, p = 1, p² = 1, and p³ = 1 (from the first row of the table) gives

$$\eqalign{  & 6 v^3  = 2nnn - 0 - 2n  \cr   & \quad \quad \quad \quad  + 3nn - 3n  \cr   & \quad \quad \quad \quad \quad \quad \; + 6n - 6  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \; + 6 \cr} $$

or  $$ v^3  = {{2nnn + 3nn + n} \over 6} = {{n(n + 1)(2n + 1)} \over 6},$$

the sum of the squares of the first n positive integers.  The formula for v² with e = 2, p = 1, and p² = 1 gives

$$\eqalign{  & 2 v^2  = 2nn - 2n  \cr   & \quad \quad \quad \quad  + 2n - 2  \cr   & \quad \quad \quad \quad \quad \quad  + 2 \cr} $$

or  v²  = nn = n², as expected, and the formula for v¹ with e = 2 and p = 1 gives

$$\eqalign{  & 1 v^1  = 2n - 2  \cr   & \quad \quad \quad \; + 1 \cr} $$

or  v¹  = 2n – 1.

The table at upper right in Figure 9 contains cubes in its second column and sums of cubes in its first column.  With e = 6, p = 0, p² = 1, p³ = 1, and p⁴ = 1, we have

$$\eqalign{  & 6 v^3  = 6nnn - 0 - 6n  \cr   & \quad \quad \quad \quad \quad \quad  + 6n - 6  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad  + 6 \cr} $$

$$ \Rightarrow \quad  v^3  = nnn = n^3, $$

and, for the sum of cubes,

$$\eqalign{  & 24 v^4  = 6nnnn + 12nnn - 6nn - 12n  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad  + 12nn - 12n  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad  + 24n - 24  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\; + 24 \cr} $$

$$ \Rightarrow \quad  v^4  = {{6nnnn + 12nnn + 6nn} \over {24}} = {{n^2 (n + 1)^2 } \over 4}.$$

At folio 240, Harriot cited page 25 of Francisco Maurolico’s 1575 Arithmeticorum Libri Duo, copying out the following theorem.

The square of every triangular number is equal to the sum of cubes from unity (one) through the cube of the side of the triangle.  (Harriot, f. 240, and Maurolico, p. 25, my translation from Latin to English)

In modern symbols, $$(1 + 2 + 3 +  \cdots  + n)^2  = 1^3  + 2^3  + 3^3  +  \cdots  + n^3,$$

or $$1^3  + 2^3  + 3^3  +  \cdots  + n^3  = \left( {{{n(n + 1)} \over 2}} \right)^2 $$

for every positive integer n. 

The remaining table in Figure 9 contains fourth powers (square-squares) in its second column and sums of fourth powers in its first column.  With e = 24, p = – 12,  p² = 2, p³ = 1, p⁴ = 1, and p⁵ = 1, we have

$$\eqalign{  & 24 v^4  = 24nnnn + 48nnn - 24nn - 48n  \cr   & \quad \quad \quad \quad \quad \quad  - 48nnn - 0 + 48n  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \; + 24nn - 24n  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad  + 24n - 24  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \; + 24 \cr} $$

$$ \Rightarrow \quad  v^4  = nnnn = n^4, $$

and, for the sum of fourth powers, $$\eqalign{  & 120 v^5  = 24nnnnn + 120nnnn + 120nnn - 120nn - 144n  \cr   & \quad \quad \quad \quad \quad \quad \quad  - 60nnnn - 120nnn + 60nn + 120n  \cr  & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad  + 40nnn - 0 - 40n  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad  + 60nn - 60n  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; + 120n - 120  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \;\quad \quad  + 120 \cr} $$

implying that  $$ v^5  = {{24nnnnn + 60nnnn + 40nnn - 4n} \over {120}} = {{n^5 } \over 5} + {{n^4 } \over 2} + {{n^3 } \over 3} - {n \over {30}}.$$

(In all of these computations, the exponents on n are modern.  Harriot always wrote, for instance, nnn where we would write n³.)

When Harriot listed his resulting formulas for sums of units, positive integers, squares, cubes, and square-squares, he replaced v⁰,  v¹, v², v³, and v⁴ with “s” (for sum) followed by, respectively, a dot, line segment, small square, small cube, and his square-square symbol from Recorde.  He recorded his formula for the sum of squares, for instance, as s (square) : 6 = 2nnn + 3nn + 1n.  Although the computations are long, they are easy and Harriot did not show as much work as we do.  He had already done the hard work of deriving the formulas for entries of constant difference tables.  For the sum of cubes, for instance, at folio 239 Harriot wrote only

$$\eqalign{  & 6nnnn + 12nnn - 6nn - 12n  \cr   & \quad \quad \quad \quad \quad \quad  + 12nn - 12n  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad  + 24n \cr} $$

_____________________________________________ 

$$6nnnn + 12nnn + 6nn + 0n$$

and also checked that his formula for v⁴ with e = 6, p = 0, p²= 1, p³ = 1, p⁴ = 1, and n = 5 would give the correct fifth-row value of 225, before recording his final result at folio 240.  

At folio 239, the manuscript sheet on which the difference tables in Figure 9 appear, Harriot cited three pages from Maurolico’s Arithmeticorum Libri Duo, pages 52, 63, and 67.  What these three pages have in common is a list of the first five differences of the fourth powers, 1 (= 1⁴  – 0⁴), 15 (= 2⁴  – 1⁴), 65, 175, and 369 = (5⁴  – 4⁴),  which Harriot copied onto folio 239.  Although Harriot himself noted at folio 154 of the same manuscript volume that differences of squares, cubes, and fourth and higher powers are eventually constant and illustrated this property in Figure 9, his citations at folio 239 indicate that he may have hit upon the insight that a column of squares, cubes, or fourth powers could be extended to a constant difference table while studying Maurolico’s Arithmetic.

The English mathematician Henry Briggs (1561-1631), famous for his co-invention of logarithms with John Napier, lived in London at the same time as Harriot.  Briggs noted in his 1624 Arithmetica Logarithmica that differences of squares, cubes, and fourth and higher powers are eventually constant (Briggs, pp. 29-30, or Hutton, pp. 386-387), but did not extend his observation to formulas for sums of these powers.  We have never found any evidence of contact between Briggs and Harriot.  After Harriot’s death, Briggs notified Johann Kepler in 1625 of the impending publication of some of Harriot’s work (Frisch, pp. 661-662) and later, in 1630 or slightly earlier, praised Harriot’s work on “solid angles” or spherical trigonometry (Hakewill, pp. 263-264), but never referred to any other work of Harriot’s.

 

Exercise 13: Write a constant difference table in which the second column from the left contains fifth powers and the leftmost column contains sums of fifth powers beginning with 1.  Include at least four rows.  (You’ll need at least seven entries in the second column in order to obtain at least two copies of the constant difference, 120, in the rightmost column only by taking differences.)   Use Harriot’s formula for v⁶, the nth entry of your leftmost column (the column labeled p⁶), to obtain a formula for the sum of the first n fifth powers in terms of the positive integer n.

$$\eqalign{ 720 v^6 & = ennnnnn + 9ennnnn + 25ennnn + 15ennn - 26enn - 24en  \cr   & \quad \quad \quad \quad    + 6pnnnnn + 30pnnnn + 30pnnn - 30pnn - 36pn  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \, + 30 p^2 nnnn + 60 p^2 nnn - 30 p^2 nn - 60 p^2 n  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; + 120 p^3 nnn - 0 p^3 nn - 120 p^3 n  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad\quad \; \; + 360 p^4 nn - 360 p^4 n  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \;\quad \quad\quad \quad \;\; + 720 p^5 \,n - 720 p^5   \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; + 720 p^6  \cr}$$

 

Exercise 14: In order to use Harriot’s method to obtain a formula for the sum of the first n sixth powers, we would need both a constant difference table with leftmost column containing the first few sums of sixth powers and a formula for v⁷, the nth entry of the leftmost column of an eight-column constant difference table, in terms of the entries, p⁷, p⁶, p⁵, p⁴, p³, p², p, and e, of the first row of the constant difference table.  Write formulas for v⁵, v⁶, and v⁷ by noting the pattern in the following formulas for v¹, v², v³, and  v⁴: 

$$v^1  = (n - 1)e + p,$$

$$v^2  = {{n(n - 1)} \over 2}e + (n - 1)p +  p^2,$$

$$ v^3  = {{(n + 1)n(n - 1)} \over {3 \cdot 2}}e + {{n(n - 1)} \over 2}p + (n - 1) p^2  +  p^3,$$

and $$ v^4  = {{(n + 2)(n + 1)n(n - 1)} \over {4 \cdot 3 \cdot 2}}e + {{(n + 1)n(n - 1)} \over {3 \cdot 2}}p + {{n(n - 1)} \over 2} p^2  + (n - 1) p^3  +  p^4.$$

 

Solutions to these exercises are available by clicking here.

Johann Faulhaber was an arithmetic teacher (rechenmeister), who spent his entire life in Ulm, Germany. He also was an enthusiastic adherent of the new Protestantism who highlighted the number 666 in all of his books, whether religious or mathematical, and whose numerological predictions put him in constant conflict with religious and civil authorities.

In his 1631 Academia Algebrae, Faulhaber presented formulas for sums of powers of the first n positive integers from the 13^th to the 17^th powers (Faulhaber, folios Bi verso-Cii recto). He had presented formulas for sums of powers up to the seventh power in his 1614 Newer Arithmetischer Wegweyser and up to the 12^th power in his 1617 Continuatio seiner neuen Wunderkunsten (Schneider, p. 138; see also Faulhaber, ff. Aiii verso-Aiv recto). Furthermore, D.E. Knuth has argued that, in Academia Algebrae, Faulhauber actually encoded sums of powers of positive integers up to the 23^rd power (Knuth, pp. 282-283).

Figure 10. Faulhaber’s presentation of his formula for the sum of the 13^th powers in Academia Algebrae, folios Bi verso-Bii recto, is printed across a two-page spread. An electronic copy of Academia Algebrae, including folios Bi verso and Bii recto, is available from the University of Dresden Digital Library. (Reproduced by permission of Columbia University Library. For images of these two pages and the title page with rulers alongside to show size, see "Johann Faulhaber's Academia Algebrae" in "Mathematical Treasures.")

Faulhaber's formulas in his Academia Algebrae are presented both in terms of n and in terms of n(n + 1)/2. Actually, rather than being given in terms of an unknown n or x, they are presented using an early algebraic notation for powers of the unknown called "cossist" notation. Faulhaber's symbols for these powers are close to Recorde's (see Figure 8) and are listed in folio Dii verso of his Academia Algebrae, available electronically from the University of Dresden Digital Library. In his notation, the symbol for the square is a script "z" that stands for zensus (square), and the symbol for the cube a script "c" that stands for cubus (cube). The symbol for the fourth power, actually two script "z"s, stands for zensus de zensus (square of square), and that for the sixth power, "zc," zensicubus (square of cube). The symbol for the fifth power, similar to the German "ss," stands for sursolidum; for the seventh power, this symbol is preceded by a "b", so we get b-sursolidum. Similarly, Faulhaber's symbol for the eleventh power is c-sursolidum, for the 13th power d-sursolidum, and so on for the other prime powers. Continuing in this manner, we see that the 14th power symbol, then, stands for zensus de b-sursolidum (square of seventh power).

We can rewrite Faulhaber's instructions for the sum of the 13th powers (see Figure 10) in modern notation as follows:

Given n, multiply $${{n^2 + n} \over 2}$$

by 2764 to obtain 1382n² + 1382n, then subtract 691 from this expression to obtain 1382n² + 1382n – 691.

Next, subtract $${{n^4 + 2n^3 + n^2 } \over 4} \cdot 4720,$$

or $$1180n^4 + 2360n^3 + 1180n^2;$$

add $${{n^6 + 3n^5 + 3n^4 + n^3 } \over 8} \cdot 4592,$$

or $$574n^6 + 1722n^5 + 1722n^4 + 574n^3;$$

subtract $${{n^8 + 4n^7 + 6n^6 + 4n^5 + n^4 } \over {16}} \cdot 2800,$$

or $$175n^8 + 700n^7 + 1050n^6 + 700n^5 + 175n^4;$$

and add $${{n^{10} + 5n^9 + 10n^8 + 10n^7 + 5n^6 + n^5 } \over {32}} \cdot 960,$$

or $$30n^{10} + 150n^9 + 300n^8 + 300n^7 + 150n^6 + 30n^5,$$

to obtain the expression $$30n^{10} + 150n^9 + 125n^8 - 400n^7 - 326n^6 + 1052n^5 + 367n^4 - 1786n^3 + 202n^2 + 1382n - 691,$$

which we are to divide by 105. Note that $${{n^2 + n} \over 2} = {{n(n + 1)} \over 2}$$

and that the successive quotients whose products by certain numbers are being added and subtracted are $$\left( {{{n(n + 1)} \over 2}} \right)^2, \left( {{{n(n + 1)} \over 2}} \right)^3, \left( {{{n(n + 1)} \over 2}} \right)^4,\ {\rm and} \left( {{{n(n + 1)} \over 2}} \right)^5.$$

The polynomial we have obtained so far cannot be the correct formula for the sum of the 13^th powers because it is of degree 10 rather than degree 14. Faulhaber’s next instruction is to multiply the expression obtained so far by $${n^4 + 2n^3 + n^2 \over 4}\,\,\, {\rm or}\,\,\, \left(n(n + 1)\over 2 \right)^2$$

to obtain the sum of the 13^th powers, $${{30n^{14} + 210n^{13} + 455n^{12} - 1001n^{10} + 2145n^8 - 3003n^6 + 2275n^4 - 691n^2 } \over {420}}.$$

As D.E. Knuth pointed out (Knuth, p. 277), Faulhaber also described in his presentation above the formula $${{960N^7 - 2800N^6 + 4592N^5 - 4720N^4 + 2764N^3 - 691N^2 } \over {105}},$$

where N = n(n + 1)/2, for the sum of the 13^th powers. In Academia Algebrae, Faulhaber presented similar formulas for sums of 14^th through 17^th powers, and gave a formula for the sum of the eighth powers as well (f. Diii).

According to Faulhaber scholar Ivo Schneider, Faulhaber's early training as a weaver helped him see relationships between long columns containing numerical values of powers, sums of powers, and powers and products of sums of powers (see Schneider, pp. 131-139). Indeed, when these columns were arranged side-by-side, they would have resembled somewhat the warp threads – the vertical threads – in a loom, and Faulhaber's alternating pattern of addition and subtraction of terms may have corresponded, for him, to the weaving of weft threads – horizontal threads – over and under the warp threads. Even so, patterns or formulas for writing sums of 18th and higher powers have never been readily apparent to readers of Faulhaber's presentation of his formulas for sums of 13th through 17th powers in Academia Algebrae!

Pierre de Fermat, who lived most of his life in Toulouse, France, was a lawyer who spent his spare time doing mathematics. Like Harriot, he never published any of his work, but he did share hints of it in letters to Marin Mersenne, Gilles Persone de Roberval, and others. Fermat is famous for stating, but not proving, Fermat’s Last Theorem, which finally was proved by Andrew Wiles in 1994.

In letters to Mersenne and Roberval in 1636, Fermat stated the following results about the generalized triangular numbers (Mahoney, pp. 230-231):

The last side multiplied by the next greater makes twice the triangle. The last side multiplied by the triangle of the next greater side makes three times the pyramid. The last side multiplied by the pyramid of the next greater side makes four times the triangulotriangle. And so on by the same progression in infinitum.

We have seen the triangular numbers. The triangular numbers 1, 3, 6, 10, 15, 21, … are sums of successive positive integers; the pyramidal numbers 1, 4, 10, 20, 35, 56, … are sums of successive triangular numbers; the triangulotriangular numbers (as Fermat called them) 1, 5, 15, 35, 70, 126, … are sums of successive pyramidal numbers; and so on. For example, the fourth triangular number, 10, is given by 10 = 1 + 2 + 3 + 4, and the third pyramidal number, 10, is given by 10 = 1 + 3 + 6. If we denote the nth triangular number by \(T_n,\) the nth pyramidal number by \(P_n,\) and the nth triangulotriangular number by \(TT_n,\) then we can translate Fermat’s first three sentences to the following three equations in our notation: $$n(n + 1) = 2T_n,\ nT_{n + 1} = 3P_n, \ {\rm and}\ nP_{n + 1} = 4TT_n.$$

The first equation gives us the formula, $$T_n = {{n(n + 1)} \over 2}$$

for the nth triangular number or, equivalently, the sum of the first n positive integers. This result, substituted into the second equation, then yields $$n\cdot{(n + 1)(n + 2) \over 2} = 3P_n\ {\rm or}\ P_n = {n(n + 1)(n + 2)\over 2 \cdot 3}$$

for the nth pyramidal number. Finally, this last result, substituted into the third equation, gives $$TT_n = {{n(n + 1)(n + 2)(n + 3)} \over {2 \cdot 3 \cdot 4}}$$

for the nth triangulotriangular number.

In the same letters, Fermat gave two hints about sums of powers of integers. First, he wrote the following formula for the sum of the fourth powers of the first n positive integers (Mahoney, p. 231).

If you multiply four times the greatest number increased by two by the square of the triangle of numbers, and from the product you subtract the sum of the squares of the individual numbers, five times the sum of the fourth powers will result.

Translating Fermat’s words into our modern notation, we have

$$(4n + 2)\,T_n ^2 - (1^2 + 2^2 + \cdots + n^2 ) = 5(1^4 + 2^4 + \cdots + n^4 ),$$

or, substituting formulas for \(T_n\) and for $$1^2 + 2^2 + \cdots + n^2,$$

$$(4n + 2)\,\left( {{{n(n + 1)} \over 2}} \right)^2 - {{n(n + 1)(2n + 1)} \over 6} = 5(1^4 + 2^4 + \cdots + n^4 ).$$

Solving for $$1^4 + 2^4 + \cdots + n^4,$$

we get

$$1^4 + 2^4 + \cdots + n^4 = {{n(n + 1)(2n + 1)\left( {2\, \cdot {{n(n + 1)} \over 4} - {1 \over 6}} \right)} \over 5} = {{n(n + 1)(2n + 1)(3n^2 + 3n - 1)} \over {30}}$$

$$ = {{6n^5 + 15n^4 + 10n^3 - n} \over {30}} = {{n^5 } \over 5} + {{n^4 } \over 2} + {{n^3 } \over 3} - {n \over {30}}.$$

It would make sense that Fermat would report his formula for the sum of fourth powers, because it would be the first such formula he thought was unknown (Mahoney, p. 232). In his letter to Roberval, Fermat explained his use for the formulas described above (Mahoney, p. 231).

All these propositions, however pretty in themselves, have aided me in the quadrature that I’m pleased you value.

Fermat’s biographer, Michael Mahoney, has argued that, like Archimedes, Fermat’s results in “quadrature” would have required that he have verbal formulas for sums of powers of integers (Mahoney, pp. 231-233). More specifically, Fermat’s success in computing the definite integral of a function of the form cx^k would have required that he describe a formula for the sum of the kth powers of the first n positive integers. In reality, an inequality like that of Archimedes or a limit involving only terms with exponent k + 1 would have sufficed, so we cannot say with certainty that Fermat had formulas beyond the one he described for the sum of fourth powers.

Based on the evidence above, Mahoney surmised that Fermat used the following method to derive sums of powers (Mahoney, pp. 231-232). We will assume that Fermat already knew or had derived formulas for the sums of the first n positive integers and of their squares and cubes, and now wished to obtain a formula for the sum of the fourth powers of the first n positive integers. The generalized triangular numbers after the triangulotriangular numbers are sometimes called triangulopyramidal numbers. If \(TP_n\) is the nth triangulopyramidal number, then, by definition, \(TP_n\) is the sum of the first n triangulotriangular numbers; that is, $$TP_n = \sum_{k = 1}^n {TT_k }.$$

According to Fermat’s first result above and our reasoning there, $$TP_n = {{n(n + 1)(n + 2)(n + 3)(n + 4)} \over {2 \cdot 3 \cdot 4 \cdot 5}}.$$

Using our formula for \(TT_n,\) the defining equation then becomes $${{n(n + 1)(n + 2)(n + 3)(n + 4)} \over {2 \cdot 3 \cdot 4 \cdot 5}} = \sum_{k = 1}^n {{{k(k + 1)(k + 2)(k + 3)} \over {2 \cdot 3 \cdot 4}}}, $$

or $${{n(n + 1)(n + 2)(n + 3)(n + 4)} \over {2 \cdot 3 \cdot 4 \cdot 5}} = \sum_{k = 1}^n {{{k^4 + 6k^3 + 11k^2 + 6k} \over {24}}}.$$

Solving for the sum of the fourth powers, we obtain $${1 \over {24}}\sum_{k = 1}^n {k^4 } = {{n(n + 1)(n + 2)(n + 3)(n + 4)} \over {120}} - {1 \over 4}\sum_{k = 1}^n {k^3 } - {{11} \over {24}}\sum_{k = 1}^n {k^2 } - {1 \over 4}\sum_{k = 1}^n k .$$

If we now substitute our formulas for the sums of the first n positive integers and of their squares and cubes, multiply both sides of the equation by 24, and simplify, we will obtain one (or all) of the formulas for the sums of fourth powers given above.

Harriot actually wrote symbolic formulas like those labeled \(T_n,\) \(P_n,\) \(TT_n,\) and \(TP_n\) (Harriot, folios 108-109; or Beery and Stedall, pp. 58-61), but, as we have seen, he used another method to derive his formulas for sums of powers of integers. This method, explained in detail above, was described more briefly in the book by Beery and Stedall (pp. 19-20).

Exercise 15: Show how to write Fermat’s formula for the sum of the first n fourth powers as a (rational) multiple of n(n + 1)(2n + 1)/6.

Exercise 16: Write Fermat’s formula for the sixth order triangular numbers, 1, 7, 28, 84, … in words and in symbols, perhaps denoting the nth sixth order triangular number as T_n⁶. Note: The second order triangular numbers are the triangular numbers 1, 3, 6, 10, …; the third order triangular numbers the pyramidal numbers 1, 4, 10, 20, …; the fourth order triangular numbers the triangulotriangular numbers 1, 5, 15, 35, …; and the fifth order triangular numbers the triangulopyramidal numbers 1, 6, 21, 56, ….

Exercise 17: Use your formula for the nth sixth order triangular number T_n⁶ from Exercise 16, along with the formula for the nth triangulopyramidal number TP_n (or T_n⁵) and the four formulas already derived for the sums of the first n positive integers and their squares, cubes, and fourth powers, to derive a formula for the sum of the first n fifth powers.

For solutions to these exercises, click here.

The French mathematician and philosopher, Blaise Pascal, is best known in mathematics for his analysis of Pascal’s triangle (which he called the “arithmetical triangle”), for his pioneering work in what is now known as probability theory, and for inventing a calculating machine. Although Pascal corresponded with Fermat, the two mathematicians probably did not share with one another their work on sums of powers of integers, as Pascal’s approach to describing formulas for these sums was quite different from Fermat’s.

In his famous Traite du Triangle Arithmetique or Treatise on the Arithmetical Triangle, written in 1654 and published in 1665, Pascal described in words a general formula for the sum of powers of the first n terms of an arithmetic progression (Pascal, p. 39 of “X. Potestatum numericarum summa”), of which the sum of powers of the first n positive integers is a special case. What follows is Carl Boyer’s translation of this passage from Latin to English, alternating with our translation of Pascal’s words to modern symbols and to our specific situation of the sum of powers of the first n positive integers.

Given any numbers whatever in arithmetic progression, each being raised to the same (integral) power, to find the sum of these powers. (Boyer, p. 239)

Since our arithmetic progression is 1, 2, 3, 4, … , n, in what follows our first or smallest term is 1, our last term is n, our difference is 1, and our number of terms is n. If our positive integer power is m, then we are to find a formula for the sum $$1^m + 2^m + 3^m + \cdots + n^m \quad {\rm or}\quad \sum_{k = 1}^n{k^m}. $$

Form a binomial having as its first term a literal quantity A and for second term the difference of the given progression. Raise this binomial to a power of which the exponent is one more than the power proposed, noting the coefficients of the successive powers of A in the resulting development. (Boyer, p. 239)

Our instructions are to form the binomial A + 1 and then to expand (A + 1)^m+1. Using what we now call the Binomial Theorem, we have

\(\displaystyle{\left( {A + 1} \right)^{m + 1} =}\)

$$A^{m + 1} + (m + 1)A^m + {m+1\choose 2}A^{m - 1} + {m+1\choose 3}A^{m - 2} + \cdots + (m + 1)A + 1.$$

Raise to the same power as the binomial the number which in the progression follows immediately after the last given term. From the result obtained subtract the following:

1^st. The first term of the progression – that is, the smallest of the given terms, itself raised to this same power (one greater than the degree proposed).

2^nd. The difference of the progression raised to this same power, then multiplied by the number of given terms.

3^rd. The sums of similar powers of degree lower than the degree proposed, multiplied, respectively, by the coefficients of the same powers of A in the development of the above binomial. (Boyer, p. 239)

From (n + 1)^m+1, we are to subtract first 1^m+1, second 1^m+1n = n, and third

$${m+1\choose 2}\sum_{k = 1}^n k^{m - 1} +{m+1\choose 3}\sum_{k = 1}^n k^{m - 2} + \cdots + (m + 1)\sum_{k = 1}^n k,$$

to obtain the expression

$$(n + 1)^{m + 1} - \left(1 + n + {m+1\choose 2}\sum_{k = 1}^n k^{m - 1} +{m+1\choose 3}\sum_{k = 1}^n k^{m - 2}+\cdots + (m + 1)\sum_{k = 1}^n k\right).$$

The remainder found is a multiple of the sum sought, and contains this sum as many times as unity is contained in the coefficient of the power of A of which the exponent is equal to the degree of the power proposed. (Boyer, p. 239)

Since the coefficient of A^m is m + 1, the result (“remainder”) of the previous step is m + 1 times the “sum sought”; that is, $$(n + 1)^{m + 1} - \left(1 + n + {m+1\choose 2}\sum_{k = 1}^n k^{m - 1}+{m+1\choose 3}\sum_{k = 1}^n k^{m - 2}+\cdots + (m + 1)\sum_{k = 1}^n k\right)$$

\( = (m+1)\,\left( 1^m + 2^m + 3^m + \cdots + n^m\right). \)

Dividing both sides of this equation by m + 1 results in a formula for the sum \(1^m + 2^m + 3^m + \cdots + n^m\) in terms of the sums of all smaller powers of the same integers. Thus if we want to use this formula to write a polynomial expression for the sum of the fifth powers, then we must first have computed polynomial expressions for the sums of the integers, the squares, the cubes, and the fourth powers.

Just before stating the general formula or algorithm given above, Pascal illustrated both how and why it worked by using it to compute 5³ + 8³ + 11³ + 14³ (Pascal, pp. 36-38). Note that his arithmetic progression was 5, 8, 11, 14, with first term 5, last term 14, difference 3, and number of terms n = 4, and his exponent was m = 3. His final result was

17⁴

– 5 – 8 – 11 – 14 multiplied by 108

– 5² – 8² – 11² – 14² multiplied by 54

– 81 – 81 – 81 – 81

– 5⁴

equals 5³ + 8³ + 11³ + 14³ multiplied by 12 (Pascal, p. 38),

or, in more modern notation, 17⁴ – 108(5 + 8 + 11 + 14)

– 54(5² + 8² + 11² + 14²)

– 81(4)

– 5⁴

= 12(5³ + 8³ + 11³ + 14³).

The formula in the second-to-last paragraph often is written as $$(n + 1)^{m + 1} - (n + 1) = {m+1\choose 2}\sum_{k = 1}^n k^{m - 1}+{m+1\choose 3}\sum_{k = 1}^n k^{m - 2}+\cdots + (m + 1)\sum_{k = 1}^n k.$$

A.W.F. Edwards outlined Pascal’s justification for the case m = 3 as follows (Edwards, pp. 82-83). Again, in his actual justification, Pascal used the numerical example above with just four terms, but with an arithmetic progression more complicated than 1, 2, 3, 4. From the Binomial Theorem or direct computation, $$(x + 1)^4 - x^4 = 4x^3 + 6x^2 + 4x + 1.$$

Substituting x = 1, 2, 3, …, n gives the list of n equations shown below. Summing these n equations gives the equations shown below the line, which can be solved for the sum of the cubes:

$$\quad 2^4 - 1^4 = 4 \cdot 1^3 + 6 \cdot 1^2 + 4 \cdot 1 + 1$$

$$\quad 3^4 - 2^4 = 4 \cdot 2^3 + 6 \cdot 2^2 + 4 \cdot 2 + 1$$

$$\quad 4^4 - 3^4 = 4 \cdot 3^3 + 6 \cdot 3^2 + 4 \cdot 3 + 1$$

$$\quad \quad \vdots \quad \quad \quad \vdots \quad \quad \quad$$

$$(n + 1)^4 - n^4 = 4 \cdot n^3 + 6 \cdot n^2 + 4 \cdot n + 1$$

___________________________________________________________

$$\quad (n + 1)^4 - 1^4 = 4\sum_{k = 1}^n {k^3} + 6\sum_{k = 1}^n {k^2} + 4\sum_{k = 1}^n k + \sum_{k = 1}^n 1 $$

$${\rm or}\ (n + 1)^4 - (n + 1) = 4\sum_{k = 1}^n {k^3 } + 6\sum_{k = 1}^n {k^2 } + 4\sum_{k =1}^n k \quad $$

This argument can be generalized from m = 3 to any positive integer exponent m greater than or equal to 2.

Exercise 18: Apply Pascal’s written instructions for computing the sum of the powers of the first n terms in an arithmetic progression to the power 3 and the arithmetic progression 5, 8, 11, 14. That is, show how to apply Pascal’s instructions to compute 5³ + 8³ + 11³ + 14³.

Exercise 19: Use Pascal’s formula

$$\left( {n + 1} \right)^{m + 1} - \left( {1 + n + {m+1\choose 2}\sum_{k = 1}^n {k^{m - 1} } + {m+1\choose 3}\sum_{k = 1}^n {k^{m - 2} } + \cdots + (m + 1)\sum_{k = 1}^n k } \right)$$

\( = (m+1)\,\left( 1^m + 2^m + 3^m + \cdots + n^m\right) \)

with m = 5 to derive a formula for the sum of the first n fifth powers, $$\sum_{k = 1}^n {k^5 }.$$

Exercise 20: Give A.W.F. Edwards’ justification for Pascal’s case m = 5. Begin by expanding $$(x + 1)^6 - x^6.$$

Solutions to these exercises can be found by clicking here.

Jakob Bernoulli was born in Basel, Switzerland, to a large family that would become well known for its mathematical talents. He and his younger brother, Johann Bernoulli (1667-1748), the best known mathematicians in the family, had a relationship that was at times collaborative and at times contentious. Both brothers carried on Leibniz’s work in calculus and supported Leibniz in his priority dispute with Newton.

Bernoulli’s book on probability, Ars Conjectandi, was published posthumously in 1713. In it, Bernoulli derived symbolic formulas for the sums of positive integer powers using the method conjectured above for Fermat, then noted a pattern that would make computation of these formulas much simpler (Bernoulli, pp. 95-98, or Smith, pp. 85-90). Bernoulli first showed how to find the sum of the first n positive integers, obtaining $$\int n = {1 \over 2}\,nn + {1 \over 2}\,n$$

(Smith, p. 87). (Note that he used an integral sign, where we use a "sum" sign.) He then derived the sums of the first n squares and cubes, obtaining $$\int nn = {1\over 3}\,n^3 + {1\over 2} \,nn + {1 \over 6}\,n \quad {\rm and} \quad \int n^3 = {1 \over 4}\,n^4 + {1 \over 2}\,n^3 + {1 \over 4}\,nn$$

(Smith, pp. 87-89). To obtain the sum of the first n cubes, Bernoulli noted first that the general term in the fourth column of his “table of combinations” (see Fig. 11) was $${{n - 1.\,n - 2.\,n - 3} \over {1.2.3}} = {{n^3 - 6nn + 11n - 6} \over 6}.$$

1		0		0		0		0		0		0
1		1		0		0		0		0		0
1		2		1		0		0		0		0
1		3		3		1		0		0		0
1		4		6		4		1		0		0
1		5		10		10		5		1		0
1		6		15		20		15		6		1
1		7		21		35		35		21		7

Figure 11. Bernoulli’s “Table of Combinations” (Bernoulli, p. 87, or Smith, pp. 86-87)

We would write the expression on the left side of this equation as $${{(n - 1)(n - 2)(n - 3)} \over {1 \cdot 2 \cdot 3}}\quad {\rm or} \quad {n-1\choose 3}.$$

Bernoulli then noted that the sum of all terms in the fourth column up to this term (equivalently, the next term in the fifth column) was $${{n.\,n - 1.\,n - 2.\,n - 3} \over {1.2.3.4}} = {{n^4 - 6n^3 + 11nn - 6n} \over {24}}.$$

Using his summation (integral) notation, he then had

$$\int {n^3 - 6nn + 11n - 6 \over 6} = {n^4 - 6n^3 + 11nn - 6n \over 24}$$

or $$\int {1 \over 6}\,n^3 = {n^4 - 6n^3 + 11nn - 6n \over 24} + \int nn - \int {11 \over 6}\,n + \int 1.$$

Noting that \(\int 1 = n\) and using the formulas for the sums of the integers and their squares given above and then multiplying by 6, Bernoulli obtained the polynomial formula for the sum of the cubes given above. He then noted, “Thus we can step by step reach higher and higher powers . . ..” (Smith, p. 89), and provided a table of formulas for sums of powers up to

$$\int n^{10} = {1 \over 11}\,n^{11} + {1 \over 2}\,n^{10} + {5 \over 6}\,n^9 - 1\,n^7 + 1\,n^5 - {1 \over 2}\,n^3 + {5 \over 66}\,n.$$

From the formulas given above for the sums of the integers, their squares, cubes, and tenth powers, we might conjecture that a formula for the sum of the cth powers, where c is any positive integer, would have first and second terms $${1 \over {c + 1}}n^{c + 1} + {1 \over 2}n^c.$$

It would be more difficult to see that the remaining powers of n are $$n^{c - 1} ,\;n^{c - 3} ,\;n^{c - 5} ,\; \ldots ,\;n$$

for c even and $$n^{c - 1} ,\;n^{c - 3} ,\;n^{c - 5} ,\; \ldots ,\;nn$$

for c odd, and it would be nearly impossible to see what Bernoulli saw; namely, that the coefficients of these terms involve what soon would become known as Bernoulli numbers. Bernoulli gave the formula

\(\displaystyle\int n^c = {1 \over {c + 1}}n^{c + 1} + {1 \over 2}n^c + {c \over 2}An^{c - 1} + {{c.\,c - 1.\,c - 2} \over {2.3.4}}Bn^{c - 3}\, +\) $${{c.\,c - 1.\,c - 2.\,c - 3.\,c - 4} \over {2.3.4.5.6}}Cn^{c - 5} + {{c.\,c - 1.\,c - 2.\,c - 3.\,c - 4.\,c - 5.\,c - 6} \over {2.3.4.5.6.7.8}}Dn^{c - 7} ... $$

“and so on” (Smith, pp. 88, 90). His instructions for computing the Bernoulli numbers, A, B, C, …, were as follows.

The capital letters A, B, C, D denote in order the coefficients of the last terms in the expressions for $$\int nn\ ,\ \int n^4\ ,\ \int n^6\ ,\ \int n^8\ ,$$

etc., namely, A is equal to 1/6, B is equal to –1/30, C is equal to 1/42, D is equal to –1/30, ...

These coefficients are such that each one completes the others in the same expression to unity. Thus D must have the value –1/30 because

$${1 \over 9} + {1 \over 2} + {2 \over 3} - {7 \over 15} + {2 \over 9} + ( { + D}) - {1 \over 30} = 1.$$

(Smith, p. 90)

Here, Bernoulli used $$A = {1 \over 6}, \ B = - {1 \over {30}}, \ C = {1 \over {42}},$$

and c = 8 in his formula for the sum of the cth powers. We would write the sum of the coefficients as $${1 \over 9} + {1 \over 2} + {2 \over 3} - {7 \over {15}} + {2 \over 9} + D = 1$$

and solve for D, obtaining D = – 1/30. We can see from the formula above for the sum of the 10th powers or by computing directly that the next Bernoulli number, E, has the value E = 5/66.

With values for the Bernoulli numbers A, B, C, D, and E and Bernoulli’s formula for the sum of the cth powers in hand, we can write formulas for the sums of the 10th and 11th powers and we can compute the next Bernoulli number F. This, in turn, would allow us to write formulas for the sums of the 12th and 13th powers and to compute the next Bernoulli number G, and so on. Note that if we wanted a formula for, say, the sum of the 43rd powers, we would not have to compute formulas for all the sums of lower degree powers. However, we would have to compute the first 21 Bernoulli numbers and computing the first 21 Bernoulli numbers involves computing the coefficients in the formulas for the 21 sums of the cth powers with c even and between 2 and 42.

We encourage you to read the passage in which Bernoulli derived formulas for sums of positive integer powers (Smith, pp. 85-90, or Struik, pp. 316-320). The translation from Latin to English in both sources is by Jekuthiel Ginsburg of Yeshiva College (now part of Yeshiva University).

Exercise 21: Use Bernoulli’s formula for

$$\int {n^c } \quad ({\rm or}\quad \sum_{k = 1}^n {k^c })$$

to write formulas for $$\int {n^4 } = \sum_{k = 1}^n k^4 , \int {n^5 }=\sum_{k = 1}^n {k^5 }, \quad {\rm and} \quad \int n^{11} = \sum_{k = 1}^n k^{11}.$$

Exercise 22: Use Bernoulli’s formula for $$\int {n^c }\quad ({\rm or} \quad \sum_{k = 1}^n {k^c })$$

to write a formula for $$\int n^{12} =\sum_{k = 1}^n k^{12}.$$

Note that you will need to compute the Bernoulli number F in order to write this formula.

Solutions to these exercises may be found by clicking here.

Sums of powers of positive integers have been of interest to mathematicians since antiquity. Over the years, mathematicians in various places have given verbal formulas for the sum of the first n positive integers, the sum of the squares of the first n positive integers, the sum of the cubes of the first n positive integers, and so on. Beginning as early as the tenth or eleventh century, general methods existed. However, since each sum depended on the sums of the lower powers and required extensive new calculation, often done entirely verbally, in practice, these general methods did not result in calculation of formulas for sums of very high powers. Thomas Harriot seems to have been the first to derive and write formulas for sums of powers using symbolic notation, but even he calculated only up to the sum of the fourth powers. Johann Faulhaber used some symbolic notation and must have spent months, if not years, calculating formulas for sums of powers up to the 17^th power for his 1631 Academia Algebrae. Jakob Bernoulli also may have spent months or years calculating formulas for sums of powers up to the tenth power, but at some point he hit upon the pattern needed to compute relatively quickly and easily the coefficients of the formula for the sum of the cth powers for any positive integer c. Although his method required one to have computed sums of lower powers, or at least to have recorded the Bernoulli numbers, it was efficient enough that Bernoulli himself accomplished the following amazing feat.

With the help of this table, it took me less than half of a quarter of an hour to find that the tenth powers of the first 1000 numbers being added together will yield the sum 91,409,924,241,424,243,424,241,924,242,500. (Smith, p. 90)

Today we might write Bernoulli’s formula for the sum of the cth powers as $$\sum_{k = 1}^n {k^c } = {1 \over {c + 1}}\sum_{m = 0}^c {c+1\choose m}B_m n^{c + 1 - m} $$

with the Bernoulli numbers B_m defined recursively by $$B_0 = 1;\, B_1 = {1 \over 2};\, {1 \over {m + 1}}\sum_{i = 0}^m {m+1\choose i}B_i = 1$$

for m even and at least 2; and B_m = 0 for m odd and at least 3. Actually, $${1 \over {m + 1}}\sum_{i = 0}^m {m+1\choose i}B_i = 1$$

defines the Bernoulli numbers recursively for every nonnegative integer m. The first several Bernoulli numbers defined by this formula are B₀ = 1, B₁ = 1/2, B₂ = 1/6, B₃ = 0, B₄ = –1/30, B₅ = 0, B₆ = 1/42, B₇ = 0, B₈ = –1/30, B₉ = 0, B₁₀ = 5/66, B₁₁ = 0, …. For more modern formulas for sums of powers and Bernoulli numbers, see the article by Apostol, especially pp. 178-179.

Acknowledgments: We are grateful to Patricia Cornez (instructor) and Michael Camp (student), of the University of Redlands Department of Computer Science, for preparing the animations for this article; to John Navarrette, student of mathematics and of German at the University of Redlands, for his assistance with translation; and to Sandra Richey, of the University of Redlands Library, for obtaining books and journals from libraries near and far. We thank the British Library and Huntington Library for the use of manuscripts and rare books, the University of Dresden Digital Library for the use of a digital copy of Academia Algebrae, and Columbia University for permission to use a digital image from Academia Algebrae. Finally, we thank the editors of Convergence, Victor Katz and Frank Swetz, for their encouragement and assistance.

– Apostol, Tom M., 2008, “A Primer on Bernoulli Numbers and Polynomials,” Mathematics Magazine 81:3, 178-190.

– Baron, Margaret E., 1987, The Origins of the Infinitesimal Calculus, New York: Dover; first published by Pergamon Press, Oxford, 1969.

– Beery, Janet, and Jacqueline Stedall, 2009, Thomas Harriot’s Doctrine of Triangular Numbers: the “Magisteria Magna”, Zurich: European Mathematical Society.

– Bernoulli, Jakob, 1713, Ars Conjectandi, Basel.

– Boyer, Carl B., 1943, “Pascal’s Formula for the Sums of Powers of the Integers,” Scripta Mathematica 9, 237-244.

– Briggs, Henry, 1624, Arithmetica Logarithmica, London.

– Edwards, A.W.F., 1987, Pascal’s Arithmetical Triangle, London: Charles Griffin.

– Edwards, C. H., 1980, The Historical Development of the Calculus, New York: Springer.

– Faulhaber, Johannes, 1631, Academia Algebrae, Augsburg; accessed through University of Dresden Digital Library, http://digital.slub-dresden.de/en/sammlungen/titeldaten/272635758/

– Frisch, Christian (editor), 1858-1872, Joannis Kepleri Astronomi Opera Omnia, Vol. IV, Frankfurt.

– Hakewill, George, 1630, An Apologie of the Power and Providence of God in the Government of the World (2^nd ed.), Oxford.

– Harriot, Thomas, “De Numeris Triangularibus et inde De Progressionibus Arithmeticis,” British Library Additional MS 6782, ff. 107-146v.

– Harriot, Thomas, “Ad aggregata [Squares], [Cubes], [Square-squares], et c. (For Sums of Squares, Cubes, Square-squares, Etc.),” British Library Additional MS 6782, ff. 239-240v.

– Harriot, Thomas, “Ad Progressiones,” British Library Additional MS 6782, ff. 234-236.

– Heath, Thomas L., 1981, A History of Greek Mathematics, Vol. II, New York: Dover; first published by Clarendon Press, Oxford, 1921.

– Hutton, Charles, 1812, Tracts on Mathematical and Philosophical Subjects, Vol. I, London.

– Katz, Victor, 1998, A History of Mathematics: An Introduction (2^nd ed.), Reading, Mass.: Addison-Wesley.

– Knuth, Donald E., 1993, “Johann Faulhaber and Sums of Powers,” Mathematics of Computation 61:203, 277-294.

– Mahoney, Michael, 1994, The Mathematical Career of Pierre de Fermat (2^nd ed.), Princeton University Press.

– Maurolico, Francisco, 1575, Arithmeticorum Libri Duo, Venice.

– Nelsen, Roger B., Proofs Without Words, 1993, Washington, DC: Mathematical Association of America.

– Pascal, Blaise, 1665, Traite du Triangle Arithmetique, Paris.

– Recorde, Robert, 1557, Whetstone of Witte, London; reprinted 1969, New York: Da Capo Press.

– Schneider, Ivo, 1993, Johannes Faulhaber (1580-1635): Rechenmeister in einer Welt des Umbruchs, Basel: Birkhauser.

– Smith, David Eugene (editor), 1964, A Source Book in Mathematics, New York: Dover; first published by McGraw-Hill, 1929.

– Stein, Sherman, 1999, Archimedes: What Did He Do Besides Cry Eureka?, Washington, DC: Mathematical Association of America.

– Struik, D. J. (editor), 1969, A Source Book in Mathematics (1200-1800), Cambridge, Mass.: Harvard University Press.

Exercise 1.

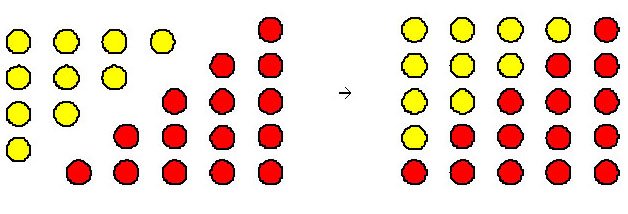
Figure 12. The sum of the 4^th and 5^th triangular numbers is the 5^th square number.

Figure 12 illustrates that the sum of the 4^th and 5^th triangular numbers is the 5^th square number (or the square of side length 5), or that 10 + 15 = 25 = 5². That 6 + 10 = 16 = 4² and 15 + 21 = 36 = 6² can be illustrated in similar fashion. The general relationship can be expressed as T_n + T_n+1 = (n+1)², where T_n is the nth triangular number, or, since T_n = n(n + 1)/2, as $${{n(n + 1)} \over 2} + {{(n + 1)(n + 2)} \over 2} = (n + 1)^2.$$

The latter equation can be checked easily using algebra.

Exercise 2.

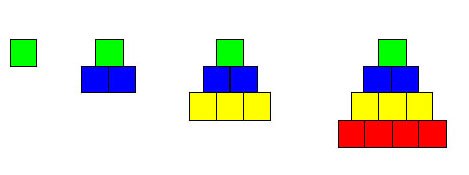
Figure 13. The first four triangular numbers represented using squares

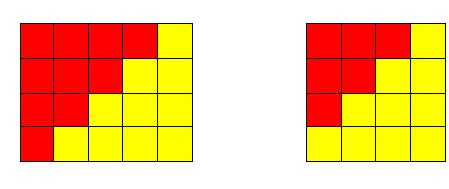
Figure 14. The identity \( 1 + 2 + 3 + ... + n = \frac{n(n + 1)}{2}\) for n = 4 (left),
and the identity from Exercise 1 for n = 3 (right)

Exercise 3. Six pyramids constructed of 1 + 3 + 6 + 10 = 20 cubes each can be fitted together to form a rectangular solid of dimensions 4 x 5 x 6, or 120 cubes in all, as shown in Figure 15. This construction illustrates that 6(1 + 3 + 6 + 10) = 4 x 5 x 6 or that \( 1 + 3 + 6 + 10 = \frac{4\times 5\times 6}{6}.\) In general, we have $$6\left( {1 + 3 + 6 + \cdots + {{n(n + 1)} \over 2}} \right) = n(n + 1)(n + 2)$$ or $$1 + 3 + 6 + \cdots + {{n(n + 1)} \over 2} = {{n(n + 1)(n + 2)} \over 6}.$$

Exercise 4. For n = 3, three shells constructed of 6 • 1² = 6 cubes, 6 • 2² = 24 cubes, and 6 • 3² = 54 cubes fit together to form a 3 x 4 x 7 rectangular solid, as shown in Figure 16A. This construction illustrates that $$6\left(1^2 + 2^2 + 3^2\right) = {3\cdot 4\cdot 7},$$ or $$1^2 + 2^2 + 3^2 = {{3\cdot 4\cdot 7} \over 6},$$ or, more generally, $$1^2 + 2^2 + 3^2 + \cdots + n^2 = {{n(n + 1)(2n + 1)} \over 6}$$ for any positive integer n.

Nilakantha reasoned that the outside shell contained 6 • 3² = 54 cubes as follows (see Figure 16B):

Exercise 5. For n = 3, three shells constructed of 6 • (1 • 2)/2 = 6 cubes, 6 • (2 • 3)/2 = 18 cubes, and 6 • (3 • 4)/2 = 36 cubes fit together to form a 3 x 4 x 5 rectangular solid, as shown in Figure 17A. This construction illustrates that $$6\left(1 + 3 + 6\right) = {3\cdot 4\cdot 5},$$ or $$1 + 3 + 6 = \frac {3\cdot 4\cdot 5}{6},$$ or, more generally, $$1 + 3 + 6 + \cdots + {{n(n + 1)} \over 2} = {{n(n + 1)(n + 2)} \over 6}$$ for any integer n.

Nilakantha may have reasoned that the outside shell contained 6 • (3 • 4)/2 = 36 cubes as follows (see Figure 17B):

Exercise 6. They may have made the following computations.

1 + 3 = 4 = 2²

3 + 6 = 9 = 3²

6 + 10 = 16 = 4²

10 + 15 = 25 = 5²

15 + 21 = 36 = 6²

The general relationship can be expressed as

T_n + T_n+1 = (n+1)²,

where T_n is the nth triangular number, or as

$${{n(n + 1)} \over 2} + {{(n + 1)(n + 2)} \over 2} = (n + 1)^2.$$

The latter equation can be checked easily using algebra.

Exercise 7.

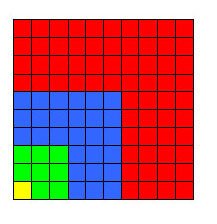
Figure 18. (1 + 2 + 3 + 4)² = 1³ + 2³ + 3³ + 4³

$$(1 + 2 + 3 + 4)^2 = (1 + 2 + 3)^2 + \left( {2 \cdot 4(1 + 2 + 3) + 4^2 } \right) \quad\quad {\rm (Step\ 1)}$$

$$= (1 + 2 + 3)^2 + \left( {2 \cdot 4{{3 \cdot 4} \over 2} + 4^2 } \right)$$

$$= (1 + 2 + 3)^2 + \left( {4^2 (3 + 1)} \right)$$

$$= (1 + 2 + 3)^2 + 4^3$$

$$= (1 + 2)^2 + \left( {2 \cdot 3(1 + 2) + 3^2 } \right) + 4^3 \quad\quad {\rm (Step\ 2)}$$

$$= (1 + 2)^2 + \left( {2 \cdot 3{{2 \cdot 3} \over 2} + 3^2 } \right) + 4^3$$

$$= (1 + 2)^2 + \left( {3^2 (2 + 1)} \right) + 4^3$$

$$= (1 + 2)^2 + 3^3 + 4^3$$

$$= 1 + (2 \cdot 2 \cdot 1 + 2^2 ) + 3^3 + 4^3 \quad\quad\quad {\rm (Step\ 3)}$$

$$= 1 + (2 \cdot 2^2 ) + 3^3 + 4^3$$

$$(1 + 2 + 3 + 4)^2= 1^3 + 2^3 + 3^3 + 4^3$$

Each cubic term represents a gnomon. In particular, 1³, 2³, 3³, and 4³ are, respectively, the areas of the yellow, green, blue, and red gnomons in Figure 18.

Exercise 8. $$1^4 + 2^4 + 3^4 + \cdots + n^4 = {1 \over 5}n^5 + {1 \over 2}n^4 + c_3 n^3 + c_2 n^2 + c_1 n + c_0,$$

where $$c_3 + c_2 + c_1 + c_0 = 1 - \left( {{1 \over 5} + {1 \over 2}} \right) = {3 \over {10}}.$$

Three possible formulas are

$${1 \over 5}n^5 + {1 \over 2}n^4 + {1 \over {10}}n^3 + {1 \over {10}}n^2 + {1 \over {10}}n,$$

$${1 \over 5}n^5 + {1 \over 2}n^4 + {1 \over 5}n^3 + {1 \over {10}}n, \quad {\rm and}$$

$${1 \over 5}n^5 + {1 \over 2}n^4 + {1 \over 5}n^3 + {1 \over {15}}n^2 + {1 \over {30}}n.$$

The correct formula is $$1^4 + 2^4 + 3^4 + \cdots + n^4 = {1 \over 5}n^5 + {1 \over 2}n^4 + {1 \over 3}n^3 - {1 \over {30}}n.$$

Surprised?

Exercise 9.

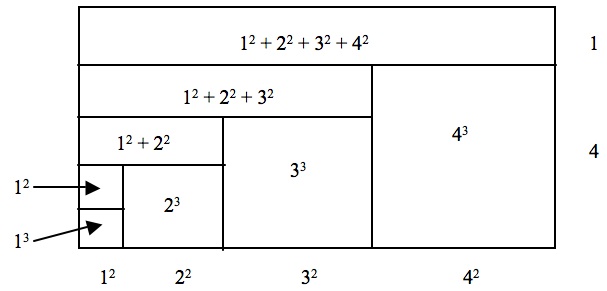
Figure 19. Each side of the equation $$(4 + 1)\sum_{i = 1}^4 {i^2 } = \sum_{i = 1}^4 {i^3 } + \sum_{p = 1}^4 {\sum_{i = 1}^p {i^2 } }$$ is the area of the rectangle.

Exercise 10. Let k = 1 in Figure 7. Then each side of the equation $$(n + 1)\sum_{i = 1}^n i = \sum_{i = 1}^n {i^2 } + \sum_{p = 1}^n {\sum_{i = 1}^p i }$$

is the area of the rectangle. Letting k = 1 in the equation $$(n + 1)\sum_{i = 1}^n {i^k} = \sum_{i = 1}^n {i^{k + 1}} + \sum_{p = 1}^n {\sum_{i = 1}^p {i^k }}$$

gives the equation $$(n + 1)\sum_{i = 1}^n i = \sum_{i = 1}^n {i^2 } + \sum_{p = 1}^n {\sum_{i = 1}^p i }$$ or

\(\displaystyle{(n + 1)(1 + 2 + 3 + \cdots + n) =}\) $$(1^2 + 2^2 + 3^2 + \cdots + n^2 ) + \sum_{p = 1}^n {(1 + 2 + 3 + \cdots + p)}$$ or

\(\displaystyle{1^2 + 2^2 + 3^2 + \cdots + n^2 =}\) $$(n + 1)(1 + 2 + 3 + \cdots + n) - \sum_{p = 1}^n {(1 + 2 + 3 + \cdots + p)}$$ or $$\eqalign{1^2 + 2^2 + 3^2 + \cdots + n^2 & = (n + 1)\left( {{{n(n + 1)} \over 2}} \right) - \sum_{p = 1}^n {{{p(p + 1)} \over 2}}\cr &= (n + 1)\left( {{{n(n + 1)} \over 2}} \right) - {1 \over 2}\sum_{p = 1}^n {p^2 } - {1 \over 2}\sum_{p = 1}^n p \cr &= (n + 1)\left( {{{n(n + 1)} \over 2}} \right) - {1 \over 2}\left( {1^2 + 2^2 + 3^2 + \cdots + n^2 } \right)}$$

\(\displaystyle{- {1 \over 2}\left( {1 + 2 + 3 + \cdots + n} \right)}\)

or $$\eqalign{{3 \over 2}\left( {1^2 + 2^2 + 3^2 + \cdots + n^2 } \right) &= (n + 1)\left( {{{n(n + 1)} \over 2}} \right) - {1 \over 2}{{n(n + 1)} \over 2}\cr &= \left( {n + {1 \over 2}} \right)\left( {{{n(n + 1)} \over 2}} \right)}$$ or $$1^2 + 2^2 + 3^2 + \cdots + n^2 = {{n(n + 1)(2n + 1)} \over 6}.$$

Exercise 11. Let k = 2 in Figure 7. Then each side of the equation $$(n + 1)\sum_{i = 1}^n i^2 = \sum_{i = 1}^n {i^3 } + \sum_{p = 1}^n {\sum_{i = 1}^p i^2}$$

is the area of the rectangle. Letting k = 2 in the equation $$(n + 1)\sum_{i = 1}^n {i^k} = \sum_{i = 1}^n {i^{k + 1}} + \sum_{p = 1}^n {\sum_{i = 1}^p {i^k }}$$

gives the equation $$(n + 1)\sum_{i = 1}^n i^2 = \sum_{i = 1}^n {i^3} + \sum_{p = 1}^n {\sum_{i = 1}^p i^2 }$$ or

\(\displaystyle{(n + 1)(1^2 + 2^2 + 3^2 + \cdots + n^2 ) =}\) $$(1^3 + 2^3 + 3^3 + \cdots + n^3 ) + \sum_{p = 1}^n {(1^2 + 2^2 + 3^2 + \cdots + p^2 )}$$ or

\(\displaystyle{1^3 + 2^3 + 3^3 + \cdots + n^3 =}\) $$(n + 1)(1^2 + 2^2 + 3^2 + \cdots + n^2 ) - \sum_{p = 1}^n {(1^2 + 2^2 + 3^2 + \cdots + p^2 )}.$$

If we now apply the formula for the sum of the squares, the equation becomes

$$1^3 + 2^3 + 3^3 + \cdots + n^3 = (n + 1)\left( {{{n(n + 1)(2n + 1)} \over 6}} \right) - \sum_{p = 1}^n {{{p(p + 1)(2p + 1)} \over 6}}$$ $$= (n + 1)\left( {{{n(n + 1)(2n + 1)} \over 6}} \right) - {1 \over 3}\sum_{p = 1}^n {p^3 } - {1 \over 2}\sum_{p = 1}^n {p^2 } - {1 \over 6}\sum_{p = 1}^n p$$

$$ = (n + 1)\left( {{{n(n + 1)(2n + 1)} \over 6}} \right) - {1 \over 3}\left( {1^3 + 2^3 + 3^3 + \cdots + n^3 } \right)$$

\(\displaystyle{- {1 \over 2}\left( {1^2 + 2^2 + 3^2 + \cdots + n^2 } \right) - {1 \over 6}\left( {1 + 2 + 3 + \cdots + n} \right)}.\)

Collecting sums of cubes and applying the formula for the sum of the squares again, we have

\(\displaystyle{{4 \over 3}\left( 1^3 + 2^3 + 3^3 + \cdots + n^3 \right) =}\) $$(n + 1)\left( {n(n + 1)(2n + 1) \over 6} \right) - {1 \over 2}{{n(n + 1)(2n + 1)} \over 6} - {1 \over 6}{{n(n + 1)} \over 2}$$ or $$\eqalign{1^3 + 2^3 + 3^3 + \cdots + n^3 &= {3 \over 4}\left( {{{n(n + 1)} \over {12}}\left( {2(n + 1)(2n + 1) - (2n + 1) - 1} \right)} \right)\cr &= {1 \over 4}\left( {{{n(n + 1)} \over 4}\left( {(2n + 1)^2 - 1} \right)} \right)\cr &= {1 \over 4}\left( {{{n(n + 1)} \over 4}\left( {4n^2 + 4n} \right)} \right)}$$ or $$1^3 + 2^3 + 3^3 + \cdots + n^3 = \left( n(n + 1) \over 2 \right)^2.$$

Exercise 12.

$$\eqalign{\left({n \over 5} + {1 \over 5} \right)n\left( n + {1 \over 2} \right)\left( (n + 1)n - {1 \over 3} \right) &={1 \over 5}(n + 1)n\left({1 \over 2} \right)(2n + 1)\left((n + 1)n - {1 \over 3} \right)\cr &={n(n + 1)(2n + 1) \over 6}\left({3 \over 5}(n + 1)n - {1 \over 5} \right).}$$

Exercise 13. The constant difference table for sums of fifth powers is in Figure 20. Blue entries are obtained from knowing that the next highest entry in the fifth powers column is 0; that is, from knowing that 0⁵ = 0. Red entries are obtained from knowing the constant difference is 120. Blue entries may be obtained in this way, too.

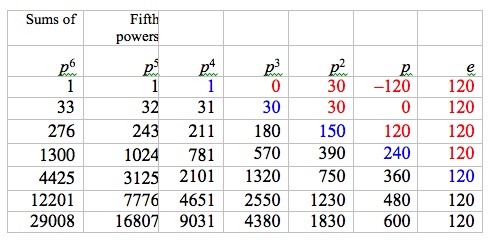
Figure 20. Constant difference table for sums of fifth powers

Substituting the values from the first row of the table in Figure 20 into Harriot’s formula for v⁶, we obtain the following:

$$\eqalign{720 v^6 &= 120nnnnnn + 1080nnnnn + 3000nnnn + 1800nnn - 3120nn - 2880n \cr & \quad \quad \quad \quad \quad \quad \;\;\; - 720nnnnn - 3600nnnn - 3600nnn + 3600nn + 4320n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \;\;\; + 900nnnn + 1800nnn - 900nn - 1800n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; + 0nnn\;\;\; - 0nn\;\;\; - 0n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \quad \quad \quad \quad \quad \; + 360nn - 360n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \;\quad \quad \quad \quad \quad \quad \quad \quad \quad + 720n - 720 \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; + 720\cr & = 120nnnnnn + 360nnnnn + 300nnnn + 0nnn - 60nn + 0n + 0\cr &= 120nnnnnn + 360nnnnn + 300nnnn - 60nn,}$$ or $$v^6 = {1 \over {720}}\left( {120nnnnnn + 360nnnnn + 300nnnn - 60nn} \right)$$ $$= {1 \over 6}nnnnnn + {1 \over 2}nnnnn + {5 \over {12}}nnnn - {1 \over {12}}nn,$$

or, in modern notation,

$$\sum_{k = 1}^n {k^5 } = {1 \over 6}n^6 + {1 \over 2}n^5 + {5 \over {12}}n^4 - {1 \over {12}}n^2.$$

Exercise 14.

We have

$$\eqalign{v^5 = & {{(n + 3)(n + 2)(n + 1)n(n - 1)} \over {5 \cdot 4 \cdot 3 \cdot 2}}e + {{(n + 2)(n + 1)n(n - 1)} \over {4 \cdot 3 \cdot 2}}p\cr & + {{(n + 1)n(n - 1)} \over {3 \cdot 2}} p^2 + {{n(n - 1)} \over {2}} p^3 + (n - 1) p^4 + p^5,}$$

$$\eqalign{v^6 & = {{(n + 4)(n + 3)(n + 2)(n + 1)n(n - 1)} \over {6 \cdot 5 \cdot 4 \cdot 3 \cdot 2}}e + {{(n + 3)(n + 2)(n + 1)n(n - 1)} \over {5 \cdot 4 \cdot 3 \cdot 2}}p\cr &+ {{(n + 2)(n + 1)n(n - 1)} \over {4 \cdot 3 \cdot 2}} p^2 + {{(n + 1)n(n - 1)} \over {3 \cdot 2}} p^3 + {{n(n - 1)} \over 2} p^4 + (n - 1) p^5 + {p^6},}$$ and

$$\eqalign{v^7 & = {{(n + 5)(n + 4)(n + 3)(n + 2)(n + 1)n(n - 1)} \over {7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2}}e\cr & + {{(n + 4)(n + 3)(n + 2)(n + 1)n(n - 1)} \over {6 \cdot 5 \cdot 4 \cdot 3 \cdot 2}}p + {{(n + 3)(n + 2)(n + 1)n(n - 1)} \over {5 \cdot 4 \cdot 3 \cdot 2}} p^2\cr & + {{(n + 2)(n + 1)n(n - 1)} \over {4 \cdot 3 \cdot 2}} p^3 + {{(n + 1)n(n - 1)} \over {3 \cdot 2}} p^4 + {{n(n - 1)} \over 2} p^5 + (n - 1) p^6 + p^7}$$ or $$v^7 = {n+5\choose 7}e + {n+4\choose 6}p + {n+3\choose 5}p^2 + {n+2\choose 4}p^3 + {n+1\choose 3}p^4$$

\(\displaystyle{+ {n \choose 2}p^5 + (n - 1) p^6 + p^7.}\)

Exercise 15. Beginning with our simplification of Fermat’s formula, we have

$${{n(n + 1)(2n + 1)(3n^2 + 3n - 1)} \over {30}} = {{n(n + 1)(2n + 1)} \over 6} \cdot {{(3n^2 + 3n - 1)} \over 5}.$$

Beginning with Fermat’s formula, we have

$$\eqalign{ & {1 \over 5}\left( {(4n + 2)\,\left( {{{n(n + 1)} \over 2}} \right)^2 - {{n(n + 1)(2n + 1)} \over 6}} \right) \cr & = {2 \over 5}(2n + 1)\,\left( {{{n(n + 1)} \over 2}} \right)^2 - {1 \over 5} \cdot {{n(n + 1)(2n + 1)} \over 6}\cr & = {{n(n + 1)(2n + 1)} \over 6}\left( {6 \cdot {2 \over 5} \cdot {{n(n + 1)} \over 4} - {1 \over 5}} \right)\cr & = {{n(n + 1)(2n + 1)} \over 6} \cdot {{(3n^2 + 3n - 1)} \over 5}. \cr}$$

Exercise 16. If T_n⁶ is the nth sixth order triangular number, then, by definition, T_n⁶ is the sum of the first n triangulopyramidal numbers; that is, $$T_n^6 = \sum_{k = 1}^n {TP_k } \quad {\rm or} \quad T_n^6 = \sum_{k = 1}^n {T_k^5 }.$$

Perhaps Fermat would have called T_n⁶ a “pyramidopyramidal number” and written, “The last side multiplied by the triangulopyramidal of the next greater side makes six times the pyramidopyramidal.” This translates to $$nTP_{n + 1} = 6T_n^6 \quad {\rm or} \quad n \cdot {{(n + 1)(n + 2)(n + 3)(n + 4)(n + 5)} \over {2 \cdot 3 \cdot 4 \cdot 5}} = 6T_n^6 \quad {\rm or}$$

$$T_n^6 = {{n(n + 1)(n + 2)(n + 3)(n + 4)(n + 5)} \over {2 \cdot 3 \cdot 4 \cdot 5 \cdot 6}}.$$

Exercise 17. Using our formulas for TP_n and T_n⁶ (from Exercise 16), the equation $$T_n^6 = \sum_{k = 1}^n {TP_k }$$

from Exercise 16 becomes $${{n(n + 1)(n + 2)(n + 3)(n + 4)(n + 5)} \over {2 \cdot 3 \cdot 4 \cdot 5 \cdot 6}} = \sum_{k = 1}^n {{{k(k + 1)(k + 2)(k + 3)(k + 4)} \over {2 \cdot 3 \cdot 4 \cdot 5}}}\quad {\rm or}$$

$${{n(n + 1)(n + 2)(n + 3)(n + 4)(n + 5)} \over {2 \cdot 3 \cdot 4 \cdot 5 \cdot 6}} = \sum_{k = 1}^n {{{k^5 + 10k^4 + 35k^3 + 50k^2 + 24k} \over {120}}}.$$

Solving for the sum of the fifth powers, we obtain

\( \displaystyle{{1 \over {120}}\sum_{k = 1}^n {k^5 } =}\)

$${{n(n + 1)(n + 2)(n + 3)(n + 4)(n + 5)} \over {720}} - {1 \over {12}}\sum_{k = 1}^n {k^4 } - {7 \over {24}}\sum_{k = 1}^n {k^3 } - {5 \over {12}}\sum_{k = 1}^n {k^2 } - {1 \over 5}\sum_{k = 1}^n k.$$

If we now substitute our formulas for the sums of the first n positive integers and of their squares, cubes, and fourth powers, multiply both sides of the equation by 120, and simplify, we will obtain a formula for the sum of the first n fifth powers as follows:

$$\eqalign{\sum_{k = 1}^n {k^5 } & = 120 \cdot {{n^6 + 15n^5 + 85n^4 + 225n^3 + 274n^2 + 120n} \over {720}}\cr & \quad - {{120} \over {12}}\left( {{{n^5 } \over 5} + {{n^4 } \over 2} + {{n^3 } \over 3} - {n \over {30}}} \right) - {{7 \cdot 120} \over {24}}\left( {{{n^4 } \over 4} + {{n^3 } \over 2} + {{n^2 } \over 4}} \right)\cr & \quad - {{5 \cdot 120} \over {12}}\left( {{{n^3 } \over 3} + {{n^2 } \over 2} + {n \over 6}} \right) - {{120} \over 5}\left( {{{n^2 } \over 2} + {n \over 2}} \right) \cr &= {1 \over 6}n^6 + {1 \over 2}n^5 + {5 \over {12}}n^4 + 0n^3 - {1 \over {12}}n^2 + 0n\cr & = {1 \over 6}n^6 + {1 \over 2}n^5 + {5 \over {12}}n^4 - {1 \over {12}}n^2.}$$

Exercise 18. We repeat Carl Boyer’s translation of Pascal’s instructions for finding the sum of powers of an arithmetic progression, so that we may more easily apply them to our arithmetic progression.

Given any numbers whatever in arithmetic progression, each being raised to the same (integral) power, to find the sum of these powers. (Boyer, p. 239)

Since our arithmetic progression is 5, 8, 11, 14, in what follows our first or smallest term is 5, our last term is 14, our difference is 3, and our number of terms is 4. Our positive integer power is 3 and we are to find a formula for the sum 5³ + 8³ + 11³ + 14³.

Form a binomial having as its first term a literal quantity A and for second term the difference of the given progression. Raise this binomial to a power of which the exponent is one more than the power proposed, noting the coefficients of the successive powers of A in the resulting development. (Boyer, p. 239)

Our instructions are to form the binomial A + 3 and then to expand (A + 3)⁴. Using the Binomial Theorem, we have

\(\displaystyle{\left( {A + 3} \right)^4 =}\)

$$A^4 + 4A^3 \cdot 3 + {4\choose 2}A^2 \cdot 3^2 + {4\choose 3}A \cdot 3^3 + 3^4 = A^4 + 12A^3 + 54A^2 + 108A + 81.$$

We are to remember the coefficients 12, 54, and 108.

Raise to the same power as the binomial the number which in the progression follows immediately after the last given term. From the result obtained subtract the following:

1^st. The first term of the progression – that is, the smallest of the given terms, itself raised to this same power (one greater than the degree proposed).

2^nd. The difference of the progression raised to this same power, then multiplied by the number of given terms.

3^rd. The sums of similar powers of degree lower than the degree proposed, multiplied, respectively, by the coefficients of the same powers of A in the development of the above binomial. (Boyer, p. 239)

From 17⁴, we are to subtract first 5⁴, second 3⁴\(\cdot\) 4, and third 54(5² + 8² + 11² + 14²) and 108(5 + 8 + 11 + 14), to obtain the expression

$$17^4 - \left( {5^4 + 3^4\cdot 4 + 54\left( {5^2 + 8^2 + 11^2 + 14^2 } \right) + 108\left( {5 + 8 + 11 + 14} \right)} \right).$$

The remainder found is a multiple of the sum sought, and contains this sum as many times as unity is contained in the coefficient of the power of A of which the exponent is equal to the degree of the power proposed. (Boyer, p. 239)

Since the coefficient of A³ is 12, the result (“remainder”) of the previous step is 12 times the “sum sought”; that is,

$$17^4 - \left( {5^4 + 3^4 \cdot 4 + 54\left( {5^2 + 8^2 + 11^2 + 14^2 } \right) + 108\left( {5 + 8 + 11 + 14} \right)} \right)$$ $$=12\left( {5^3 + 8^3 + 11^3 + 14^3 } \right).$$

Indeed, each side of the equation equals 56544, and 5³ + 8³ + 11³ + 14³ = 56544/12 = 4712.

Exercise 19. Substituting m = 5, we have $$\eqalign{6\sum_{k = 1}^n k^5 &=(n + 1)^6 - \left( 1 + n + 15\sum_{k = 1}^n k^4 + 20\sum_{k = 1}^n k^3 + 15\sum_{k = 1}^n k^2 + 6\sum_{k = 1}^n k \right) \cr &=n^6 + 6n^5 + 15n^4 + 20n^3 + 15n^2 + 6n + 1 - 1 - n\cr & \quad - 15\left({n^5 \over 5} + {n^4 \over 2} + {n^3 \over 3} - {n \over 30} \right) - 20\left({n^4 \over 4} + {n^3 \over 2} + {n^2 \over 4} \right)\cr & \quad - 15\left( {n^3 \over 3} + {n^2 \over 2} + {n \over 6} \right) - 6\left({n^2 \over 2} + {n \over 2} \right)\cr &=n^6 + 3n^5 + {5 \over 2}n^4 - {1 \over 2}n^2.}$$

Therefore, on dividing by m + 1 = 6, we get $$\sum_{k=1}^n k^5 = {1\over 6}n^6+{1\over 2}n^5 +{5\over 12}n^4-{1\over 12}n^2.$$

Exercise 20. From the Binomial Theorem or direct computation, $$(x + 1)^6 - x^6 = 6x^5 + 15x^4 + 20x^3 + 15x^2 + 6x + 1.$$

Substituting x = 1, 2, 3, …, n gives the list of n equations shown below. Summing these n equations gives the equations shown below the line, which can be solved for the sum of the fifth powers.

$$\quad 2^6 - 1^6 = 6 \cdot 1^5 + 15 \cdot 1^4 + 20 \cdot 1^3 + 15 \cdot 1^2 + 6 \cdot 1 + 1$$

$$\quad 3^6 - 2^6 = 6 \cdot 2^5 + 15 \cdot 2^4 + 20 \cdot 2^3 + 15 \cdot 2^2 + 6 \cdot 2 + 1$$

$$\quad 4^6 - 3^6 = 6 \cdot 3^5 + 15 \cdot 3^4 + 20 \cdot 3^3 + 15 \cdot 3^2 + 6 \cdot 3 + 1$$

. . . . . .

$$(n + 1)^6 - n^6 = 6 \cdot n^5 + 15 \cdot n^4 + 20 \cdot n^3 + 15 \cdot n^2 + 6 \cdot n + 1$$

______________________________________________________________________________

$$(n + 1)^6 - 1^6 = 6\sum_{k = 1}^n {k^5 } + 15\sum_{k = 1}^n {k^4 } + 20\sum_{k = 1}^n {k^3 } + 15\sum_{k = 1}^n {k^2 } + 6\sum_{k = 1}^n k + \sum_{k = 1}^n 1$$

$${\rm{or}}\quad (n + 1)^6 - (n + 1) = 6\sum_{k = 1}^n {k^5 } + 15\sum_{k = 1}^n {k^4 } + 20\sum_{k = 1}^n {k^3 } + 15\sum_{k = 1}^n {k^2 } + 6\sum_{k = 1}^n k$$

Exercise 21. According to Bernoulli’s formula,

$$\eqalign{\int n^4 & = {1 \over {4 + 1}}n^{4 + 1} + {1 \over 2}n^4 + {4 \over 2}An^{4 - 1} + {{4 \cdot 3 \cdot 2} \over {2 \cdot 3 \cdot 4}}Bn^{4 - 3} \cr &= {1 \over 5}n^5 + {1 \over 2}n^4 + {4 \over 2} \cdot {1 \over 6}n^3 + \left( { - {1 \over {30}}} \right)n = {1 \over 5}n^5 + {1 \over 2}n^4 + {1 \over 3}n^3 - {1 \over {30}}n}$$

and

$$\eqalign{\int n^5 &= {1 \over {5 + 1}}n^{5 + 1} + {1 \over 2}n^5 + {5 \over 2}An^{5 - 1} + {{5 \cdot 4 \cdot 3} \over {2 \cdot 3 \cdot 4}}Bn^{5 - 3} \cr &= {1 \over 6}n^6 + {1 \over 2}n^5 + {5 \over 2} \cdot {1 \over 6}n^4 + {5 \over 2}\left( { - {1 \over {30}}} \right)n^2 = {1 \over 6}n^6 + {1 \over 2}n^5 + {5 \over {12}}n^4 - {1 \over {12}}n^2.}$$

Students may have noticed already that, since A = 1/6, the coefficient of n^{c – 1} is c/12. According to Bernoulli’s formula,

$${\int n^{11}} = {1\over{11+1}}n^{11+1}+ {1\over 2} n^{11}+ {{11}\over 2} A n^{11 - 1}+ {{11.\,10.\,9} \over {2.3.4}}Bn^{11 - 3}+ {{11.\,10.\,9.\,8.\,7} \over {2.3.4.5.6}}Cn^{11 - 5}$$

$$+ {{11.\,10.\,9.\,8.\,7.\,6.\,5} \over {2.3.4.5.6.7.8}}Dn^{11 - 7}+ {{11.\,10.\,9.\,8.\,7.\,6.\,5.4.3} \over {2.3.4.5.6.7.8.9.10}}En^{11 - 9}$$

$$= {1 \over {12}}n^{12} + {1 \over 2}n^{11} + {{11} \over 2} \cdot {1 \over 6}n^{10} + {{11.\,10.\,9} \over {2.3.4}}\left( { - {1 \over {30}}} \right)n^8 + {{11.\,10.\,9.\,8.\,7} \over {2.3.4.5.6}} \cdot {1 \over {42}}n^6$$

$$+ {{11.\,10.\,9}\over{2.3.4}}\left( {-{1\over{30}}}\right) n^4 + {{11}\over 2} \cdot {5\over {66}}n^2$$

$$= {1 \over {12}}n^{12} + {1 \over 2}n^{11} + {{11} \over {12}}n^{10} - {{11} \over 8}n^8 + {{11} \over 6}n^6 - {{11} \over 8}n^4 + {5 \over {12}}n^2.$$

Exercise 22. According to Bernoulli’s formula,

$${\int n^{12}={1 \over {12 + 1}}n^{12 + 1} + {1 \over 2}n^{12} + {{12} \over 2}An^{12 - 1} + {{12.\,11.\,10} \over {2.3.4}}Bn^{12 - 3} + {{12.\,11.\,10.\,9.\,8} \over {2.3.4.5.6}}Cn^{12 - 5}}$$

$$+ {{12.\,11.\,10.\,9.\,8.\,7.\,6} \over {2.3.4.5.6.7.8}}Dn^{12 - 7}+ {{12.\,11.\,10.\,9.\,8.\,7.\,6.\,5.\,4} \over {2.3.4.5.6.7.8.9.10}}En^{12 - 9}$$

$$+ {{12.\,11.\,10.\,9.\,8.\,7.\,6.\,5.\,4.\,3.\,2} \over {2.3.4.5.6.7.8.9.10.11.12}}Fn^{12 -11}$$

$$= {1 \over {13}}n^{13} + {1 \over 2}n^{12} + {{12} \over 2} \cdot {1 \over 6}n^{11} + {{12.\,11.\,10} \over {2.3.4}}\left( { - {1 \over {30}}} \right)n^9 + {{12.\,11.\,10.\,9.\,8} \over {2.3.4.5.6}} \cdot {1 \over {42}}n^7$$

$$+ {{12.\,11.\,10.\,9} \over {2.3.4.5}}\left( { - {1 \over {30}}} \right)n^5 + {{12.11} \over {2.3}} \cdot {5 \over {66}}n^3 + Fn$$

$$= {1 \over {13}}n^{13} + {1 \over 2}n^{12} + n^{11} - {{11} \over 6}n^9 + {{22} \over 7}n^7 - {{33} \over {10}}n^5 + {5 \over 3}n^3 + Fn,$$

where $${1 \over {13}} + {1 \over 2} + 1 - {{11} \over 6} + {{22} \over 7} - {{33} \over {10}} + {5 \over 3} + F = 1,$$

or

$$F = 1 - {{210 + 1365 + 2730 - 5005 + 8580 - 9009 + 4550} \over {2730}} = {{2730 - 3421} \over {2730}} = - {{691} \over {2730}},$$

whence

$$\int n^{12} = {1 \over {13}}n^{13} + {1 \over 2}n^{12} + n^{11} - {{11} \over 6}n^9 + {{22} \over 7}n^7 - {{33} \over {10}}n^5 + {5 \over 3}n^3 - {{691} \over {2730}}n.$$