Student Module for 'Thinking Outside the Box'
Introduction
Perhaps one of the deepest entrenched calculus problem is the canonical box problem that students encounter when discussing applied extrema problems. In fact, Friedlander and Wilker (1980) commented, ''This question must be answered nearly a million times a year by calculus students from every corner of the globe'' (p. 282). Without a doubt, almost every recently published calculus text contains a problem similar to the following:
A sheet of cardboard is rectangular, 14 inches long and 8.5 inches wide. Congruent squares are to be cut from its four corners. The resulting piece of cardboard is to be folded and its edges taped to form an open-topped box (see figure below). How should this be done to get a box of largest possible volume?

Figure 1: Canonical Box Problem
In particular, this problem (or some derivative of it) occurs in a classic text such as Thomas (1953), Granville and Smith (1911) and Todhunter (1855) as well as modern texts such as Stewart (2008), Larson, Hostetler and Edwards (2007) and Smith and Minton (2007). But, what about this problem makes it so common and prevalent to the calculus experience? This module allows you to take a closer look at this common box problem and then presents a better box problem more consistent with modern box building techniques.
So, if you really enjoy this original box problem, an applet, called OpenBox, has been developed for this problem. For this applet, the yellow points are moveable and control the size of the sheet of cardboard and the position of the cut. A dynamical graphic contained in a grey box shows the graph of the Volume to cut length (x) function. In addition, a dynamical picture of the open box is provided to illustrate how the changes in cut length impacts the configuration of the open box.
Click Here to open the Open Box Problem applet
Warning: The OpenBox applet is best viewed in 1024 x 768 resolution or greater and may take up to a minute to load.
However in the rest of this module, you will focus on a new box problem, tied much closer to reality. In particular, you will be engaged in exploring this improved box problem and its real-world context along with activities that blend hands-on and applet-based investigations with a strong dose of analysis that culminates in other possible extensions and investigations.
The New Box Problem
A sheet of cardboard is rectangular, 14 inches long and 8.5 inches wide. If six congruent cuts (denoted in black) are to be made into the cardboard and five folds (denoted by dotted lines) made to adjoin the cuts so that the resulting piece of cardboard is to be folded to form a closeable rectangular box (see figures below). How should this be done to get a box of largest possible volume?
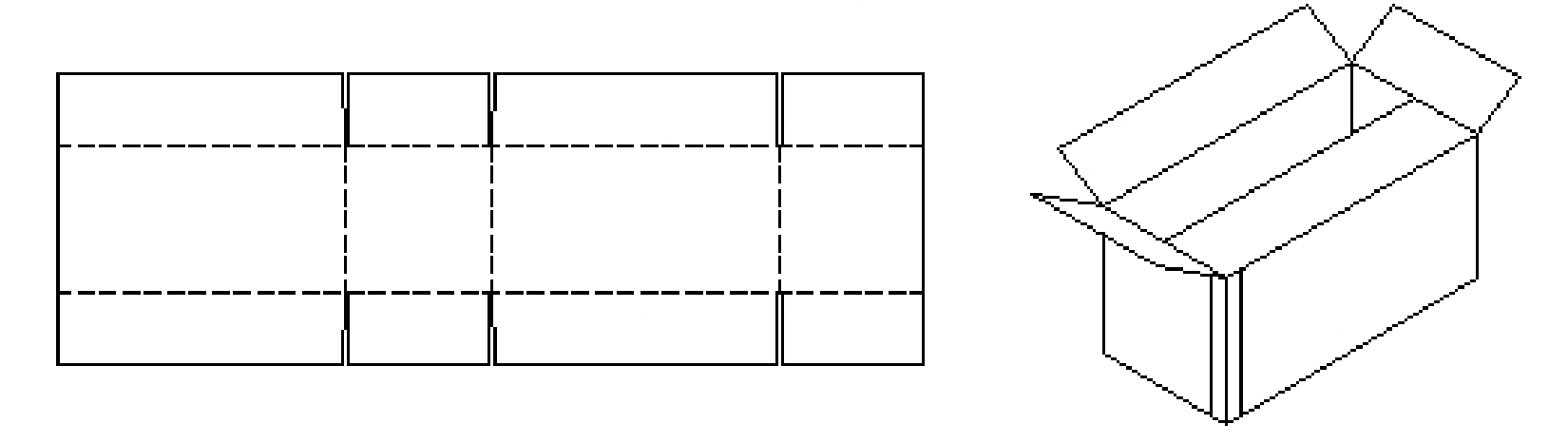
Figure 2: The box problem graphics
Before interacting with the Box problem applets and activities, you should first watch the video of such a box being manufactured and then take a rectangular piece of cardboard and attempt to physically build your own box using scissors and tape or at least find a RSC and dissect it. What did you notice from doing this activity?
Questions to be answered before moving on to the first Box problem applet and activity:
- What does a ''closeable rectangular box'' infer about the characteristics of the box?
- What impact does closeable mean with respect to the length of at least a pair of the flaps?
- Should the flaps overlap? and
- If they do overlap, is that the best use of the cardboard?
Student Module for 'Thinking Outside the Box'
Introduction
Perhaps one of the deepest entrenched calculus problem is the canonical box problem that students encounter when discussing applied extrema problems. In fact, Friedlander and Wilker (1980) commented, ''This question must be answered nearly a million times a year by calculus students from every corner of the globe'' (p. 282). Without a doubt, almost every recently published calculus text contains a problem similar to the following:
A sheet of cardboard is rectangular, 14 inches long and 8.5 inches wide. Congruent squares are to be cut from its four corners. The resulting piece of cardboard is to be folded and its edges taped to form an open-topped box (see figure below). How should this be done to get a box of largest possible volume?

Figure 1: Canonical Box Problem
In particular, this problem (or some derivative of it) occurs in a classic text such as Thomas (1953), Granville and Smith (1911) and Todhunter (1855) as well as modern texts such as Stewart (2008), Larson, Hostetler and Edwards (2007) and Smith and Minton (2007). But, what about this problem makes it so common and prevalent to the calculus experience? This module allows you to take a closer look at this common box problem and then presents a better box problem more consistent with modern box building techniques.
So, if you really enjoy this original box problem, an applet, called OpenBox, has been developed for this problem. For this applet, the yellow points are moveable and control the size of the sheet of cardboard and the position of the cut. A dynamical graphic contained in a grey box shows the graph of the Volume to cut length (x) function. In addition, a dynamical picture of the open box is provided to illustrate how the changes in cut length impacts the configuration of the open box.
Click Here to open the Open Box Problem applet
Warning: The OpenBox applet is best viewed in 1024 x 768 resolution or greater and may take up to a minute to load.
However in the rest of this module, you will focus on a new box problem, tied much closer to reality. In particular, you will be engaged in exploring this improved box problem and its real-world context along with activities that blend hands-on and applet-based investigations with a strong dose of analysis that culminates in other possible extensions and investigations.
The New Box Problem
A sheet of cardboard is rectangular, 14 inches long and 8.5 inches wide. If six congruent cuts (denoted in black) are to be made into the cardboard and five folds (denoted by dotted lines) made to adjoin the cuts so that the resulting piece of cardboard is to be folded to form a closeable rectangular box (see figures below). How should this be done to get a box of largest possible volume?

Figure 2: The box problem graphics
Before interacting with the Box problem applets and activities, you should first watch the video of such a box being manufactured and then take a rectangular piece of cardboard and attempt to physically build your own box using scissors and tape or at least find a RSC and dissect it. What did you notice from doing this activity?
Questions to be answered before moving on to the first Box problem applet and activity:
- What does a ''closeable rectangular box'' infer about the characteristics of the box?
- What impact does closeable mean with respect to the length of at least a pair of the flaps?
- Should the flaps overlap? and
- If they do overlap, is that the best use of the cardboard?
Student Module for 'Thinking Outside the Box'
The first Box Problem applet
One element in the applets that we have designed are the multiple representations and alternative ways of conveying information. For instance, the applet, ClosedBox, allows you to explore various scenarios. You can manipulate the lengths A and B by just pulling on the yellow points A' and B'. The yellow points P and Q also move. In doing so, the other components of the applet change in accordance with these manipulations. The goal here is for you to interact with a wide variety of examples and see if the conjectures they make hold up to empirical investigation. In addition, you can move the corners of the box, in the lower right-hand corner of the applet, and see if the box will actually close or not, an important aspect if you want the box to hold something. The last elements in this applet are the two different graphical indicators of maximal volume. The one graph shows the volume with respect to P or Q while the other is held constant and the bar graph next to it displays the percentage of maximal volume obtained by the current configuration. If the volume is too large, one can resize the vertical unit, a yellow point denoted by U, to get the graphs comfortably into the grey viewing window.
Click Here to open the first Box Problem applet
Warning: The first Box Problem applet page, entitled ClosedBox, is best viewed in 1024 x 768 resolution or greater and may take up to a minute to load.
You should consider the following questions as you are playing with the applet:
- Is there a relationship between the cut length and the position of the cut that maximizes the volume?
- Under what conditions does the volume drop to zero?
- Is there a best way to orient P and Q so that the maximum is achieved?
- How do the two graphics on the bottom left-hand side interact with each other?
- Why, under certain conditions, is the blue graph not connected nicely? Describe those conditions to the best of your ability.
- Why does one of the folds need to occur at the midpoint?
- What happens if the two folds aren't symmetric about the midpoint fold?
The first Box Problem activity
In the following table, carefully record the data from their various trials where the cut position, \( m( \overline {AP}) \) , is set and the cut length, \( m( \overline {BQ}) \) , is changed to maximize the volume for that particular cut position. The last row of each Trial is for you to search for the maximal cut length and the corresponding cut position. The final trial is for an open exploration of a piece of cardboard of the student's choosing.
| \( m( \overline {BQ}) \) | \( m( \overline {AP}) \) | \( m( \overline {PM}) \) | \( m( \overline {QQ'}) \) | \( m( \overline {BB'}) \) | \( m( \overline {AA'}) \) | % of max volume | |
|---|---|---|---|---|---|---|---|
| Trial 1.1 | 1.5 | 3.0 | 4.0 | 5.5 | 8.5 | 14.0 | 97.75% |
| Trial 1.2 | 3.5 | 3.5 | 8.5 | 14.0 | |||
| Trial 1.3 | 4.5 | 2.5 | 8.5 | 14.0 | |||
| Trial 1.4 | 8.5 | 14.0 | |||||
| Trial 2.1 | 2.5 | 2.5 | 10.0 | 10.0 | |||
| Trial 2.2 | 1.5 | 3.5 | 10.0 | 10.0 | |||
| Trial 2.3 | 4.25 | 0.75 | 10.0 | 10.0 | |||
| Trial 2.4 | 10.0 | 10.0 | |||||
| Trial 3.1 | 3.0 | 2.5 | 8.5 | 11.0 | |||
| Trial 3.2 | 2.75 | 2.75 | 8.5 | 11.0 | |||
| Trial 3.3 | 4.0 | 1.5 | 8.5 | 11.0 | |||
| Trial 3.4 | 8.5 | 11.0 | |||||
| Trial 4.1 | |||||||
| Trial 4.2 | |||||||
| Trial 4.3 | |||||||
| Trial 4.4 |
Exploring various positions of a cut, should lead you to a conjecture about the position of a cut and the cut length necessary to obtain the maximum volume.
Answer the following questions:
- For any positioning of the fold, the maximum volume can be best achieved when the cut length is set to?
- If the cut length exceeds the minimum of the length and width of the box, then what happens and why?
- If the cut length is less than half of the minimum of the length and width of the box, then what happens and why?
- Under what conditions is the blue graph connected above the x-axis?
- Under those conditions and for a particular length and width, what are the dimensions of the box with maximum volume?
- Why does the red graph always appear as a slanted portion? What mathematical meaning does this red graph have? Does this slanted portion ever change slope? If so, why and if not, why not?
- Using the results of your investigations and the variable l to correspond to the cut length, determine a functional description of volume taking into account the length and width of the cardboard, A and B respectively, and the variable l. Before answering this question, you might want to consider:
- How does one determine the volume of a rectangular box?
- What would be a description for the length of the box?
- What would be a description for the width of the box?
- What would be a description for the height of the box?
- How can you use these descriptions to build a functional relationship between volume and cut length?
Student Module for 'Thinking Outside the Box'
The second Box Problem applet
At first glance, this applet, ClosedBox2, contains many of the same components as the first Box Problem applet; however, the cut length determines the positioning of the cut so that in each case the box volume is relatively maximized.
Click Here to open the second Box Problem applet
Warning: The second Box Problem applet page, entitled ClosedBox2, is best viewed in 1024 x 768 resolution or greater and may take up to a minute to load.
In this applet there are a variety of elements that can be seen. First, the point P is no longer adjustable but is rather determined by the length of the cut defined by the segment BQ. In addition, the grey box in the lower left-hand of the applet contains a dynamic graphical depiction of the functional relationship between cut length and volume. That is, it contains a graphical depiction of
\[ V(l) = \left( {B - 2l} \right)\left( {{1 \over 2}A - 2l} \right)\left( {2l} \right) \]
where l corresponds to \( m( \overline {BQ} ) \) and when you intially open the applets, B = 8.5 and A = 14.0. The formula above should be equivalent to the formula you found in response to question #18.
The second Box Problem activity
Pick particular values for the length and width of the piece of cardboard, i.e. A and B, and then investigate the graph of the function on a hand-held graphing calculator. After doing so, answer the following questions:
- Why does the graphing calculator seem to show you more of the graph than the ClosedBox2 applet does?
- Why does the applet truncate the graph?
- What conditions should be on the domain of the function and how do they relate to physically constructing a box? Before answering this question, you might want to consider:
- Is the cut length constrained by the width of the piece of cardboard? If so, how and if not, why not?
- Is the cut length constrained by the length of the piece of cardboard? If so, how and if not, why not?
So far, these questions have focused primarily on a static rectangular sheet of cardboard. Now, you really need to think and explore to answer the following questions:
- For different lengths or widths, the applet's graph seems to change shape near the right-hand terminus, what mathematical reason can you provide for this change or provide an argument that it does, in fact, not change?
- Are there two (or more) non-isomorphic sheets of cardboard, so the maximal volume is the same? If so, identify them and if not, explain why not.
- Are there two (or more) non-isomorphic sheets of cardboard, so the placement of the maximal cut is the same? If so, identify them and if not, explain why not.