Logarithms: The Early History of a Familiar Function - John Napier Introduces Logarithms
In such conditions, it is hardly surprising that many mathematicians were acutely aware of the issues of computation and were dedicated to relieving practitioners of the calculation burden. In particular, the Scottish mathematician John Napier was famous for his devices to assist with computation. He invented a well-known mathematical artifact, the ingenious numbering rods more quaintly known as “Napier's bones,” that offered mechanical means for facilitating computation. (For additional information on “Napier's bones,” see the article, “John Napier: His Life, His Logs, and His Bones” (2006).) In addition, Napier recognized the potential of the recent developments in mathematics, particularly those of prosthaphaeresis, decimal fractions, and symbolic index arithmetic, to tackle the issue of reducing computation. He appreciated that, for the most part, practitioners who had laborious computations generally did them in the context of trigonometry. Therefore, as well as developing the logarithmic relation, Napier set it in a trigonometric context so it would be even more relevant.

Figure 1. John Napier (1550-1617)
(from MacTutor History of Mathematics Archive)
Napier first published his work on logarithms in 1614 under the title Mirifici logarithmorum canonis descriptio, which translates literally as A Description of the Wonderful Table of Logarithms. Indeed, the very title Napier selected reveals his high ambitions for this technique---the provision of tables based on a relation that would be nothing short of “wonder-working” for practitioners. As well as providing a short overview of the mathematical details, Napier gave technical expression to his concept. He coined a term from the two ancient Greek terms logos, meaning proportion, and arithmos, meaning number; compounding them to produce the word “logarithm.” Napier used this word as well as the designations “natural” and “artificial” for numbers and their logarithms, respectively, in his text.
Despite the obvious connection with the existing techniques of prosthaphaeresis and sequences, Napier grounded his conception of the logarithm in a kinematic framework. The motivation behind this approach is still not well understood by historians of mathematics. Napier imagined two particles traveling along two parallel lines. The first line was of infinite length and the second of a fixed length (see Figures 2 and 3). Napier imagined the two particles to start from the same (horizontal) position at the same time with the same velocity. The first particle he set in uniform motion on the line of infinite length so that it covered equal distances in equal times. The second particle he set in motion on the finite line segment so that its velocity was proportional to the distance remaining from the particle to the fixed terminal point of the line segment.
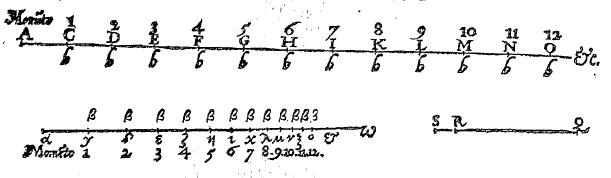
Figure 2. Napier's two parallel lines with moving particles
(Image used courtesy of Landmarks of Science Series, NewsBank-Readex)
More specifically, at any moment the distance not yet covered on the second (finite) line was the sine and the traversed distance on the first (infinite) line was the logarithm of the sine. This had the result that as the sines decreased, Napier's logarithms increased. Furthermore, the sines decreased in geometric proportion, and the logarithms increased in arithmetic proportion. We can summarize Napier's explanation as follows (Descriptio I, 1 (p. 4); see Figure 3): \[AC = \log_{nap}(\gamma\omega)\;\;{\rm where}\;\;\gamma\omega = {\rm Sin}\,\theta_{1}\]
\[AD = \log_{nap}(\delta\omega)\;\;{\rm where}\;\;\delta\omega = {\rm Sin}\,\theta_{2}\]
\[AE = \log_{nap}(\epsilon\omega)\;\;{\rm where}\;\;\epsilon\omega = {\rm Sin}\,\theta_{3}\]
and so on, so that, more generally: \[x={\rm Sin}\,(\theta)\]
\[y={\log_{nap}}(x)\] where \( \log_{nap}\) has been used to distinguish Napier's particular understanding of the logarithm concept from the modern one.
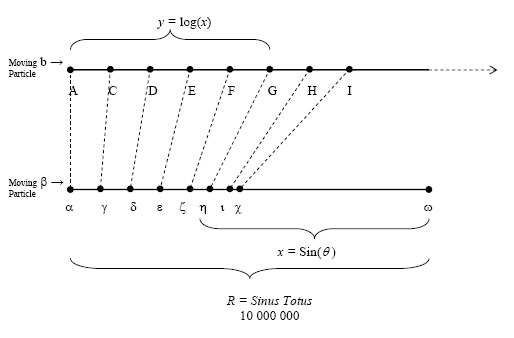
Figure 3. The relation between the two lines and the logs and sines
Napier generated numerical entries for a table embodying this relationship. He arranged his table by taking increments of arc \(\theta\) minute by minute, then listing the sine of each minute of arc, and then its corresponding logarithm. However in terms of the way he actually computed these entries, he would have in fact worked in the opposite manner, generating the logarithms first and then choosing those that corresponded to a sine of an arc, which accordingly formed the argument. For example, he would have computed values that appear in the first column of Table 1 via the relation: \[p_{n+1}=p_n\left(1-{\frac{1}{10^7}}\right)\;\;{\rm where}\;\;{p_0=10^7}.\]
| \(p_{n}\) | \(n=\log_{nap}(p_n)\) | Corresponding angle (\(\theta\)) |
| \({\bf{10000000.0000000}}\) | \(0\) | \(90^{\circ}00^{\prime}\) |
| \({\bf{9999999.0000000}}\) | \(1\) | \(89^{\circ}59^{\prime}\) |
| \({\bf{9999998.0000001}}\) | \(2\) | \(89^{\circ}58^{\prime}\) |
| \(9999997.0000003\) | \(3\) | |
| \({\bf{9999996.0000006}}\) | \(4\) | \(89^{\circ}57^{\prime}\) |
| \(9999995.0000010\) | \(5\) | |
| \(9999994.0000015\) | \(6\) | |
| \({\bf{9999993.0000021}}\) | \(7\) | \(89^{\circ}56^{\prime}\) |
| \(9999992.0000028\) | \(8\) | |
| \(9999991.0000036\) | \(9\) | |
| \(9999990.0000045\) | \(10\) | |
| \({\bf{9999989.0000055}}\) | \(11\) | \(89^{\circ}55^{\prime}\) |
Table 1. Napier's logarithms
The values in the first column (in bold) that corresponded to the Sines of the minutes of arcs (third column) were extracted, along with their accompanying logarithms (column 2) and arranged in the table. The appropriate values from Table 1 can be seen in rows one to six of the last three columns in Figure 4. Napier tabulated his logarithms from \(0^{\circ}\) to \(45^{\circ}\) in minutes of arc, and by symmetry provided values for the entire first quadrant. The excerpt in Figure 4 gives the first half of the first degree and, by symmetry, on the right the last half of the eighty-ninth degree.
To complete the tables, Napier computed almost ten million entries from which he selected the appropriate values. Napier himself reckoned that computing this many entries had taken him twenty years, which would put the beginning of his endeavors as far back as 1594.
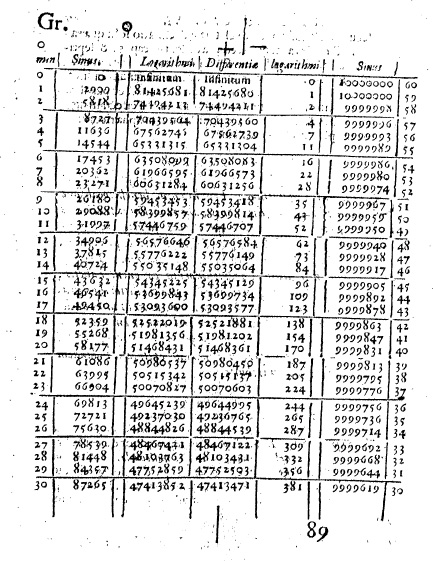
Figure 4. The first page of Napier's tables
(Image used courtesy of Landmarks of Science Series, NewsBank-Readex)
Napier frequently demonstrated the benefits of his method. For example, he worked through a problem involving the computation of mean proportionals, sometimes known as the geometric mean. He reviewed the usual way in which this would have been computed, and pointed out that his technique using logarithms not only finds the answer “earlier” (that is, faster!), but also uses only one addition and one division by two! He stated:
Let the extremes 1000000 and 500000 bee given, and let the meane proportionall be sought: that commonly is found by multiplying the extreames given, one by another, and extracting the square root of the product. But we finde it earlier thus; We adde the Logarithme of the extreames 0 and 693147, the summe whereof is 693147 which we divide by 2 and the quotient 346573 shall be the Logar. of the middle proportionall desired. By which the middle proportionall 707107, and his arch 45 degrees are found as before.... found by addition onely, and division by two. (Book I, 5 (p. 25), as translated by Edward Wright)
In order to find the mean proportional by traditional methods, Napier observed that one has to compute the product and then take the square root; that is: \[\sqrt{1 000 000 \times 500 000} = \sqrt{500 000 000 000} \approx 707106.78\] This method involves the multiplication of two large numbers and a lengthy square-root extraction. As an alternative, Napier proposed (with computations to 6 significant figures): \[\log_{nap}(1 000 000) + \log_{nap}(500 000) = 0 + 693147 = 693147\]
\[693147 \div 2 = 346573\;\;\;{\rm to}\;\;6\;\;{\rm significant}\;\;{\rm figures}\]
\[\Rightarrow {\rm mean}\;\;{\rm proportional} = 707107,\;\;\;{\rm as}\;\;{\rm required,}\] which he rightly deemed was much simpler to compute.