Combining Strands of Many Colors: Episodes from Medieval Islam for the Mathematics Classroom - Adapting Historical and Cross-cultural Examples
Many problems from cross-cultural sources are not as directly suited for classroom use as is the tassel problem discussed above. Teachers can opt to formulate their own examples, but they should also consider recasting the original ones.
Such recasting presented a fun challenge for me in Business Calculus. In my syllabus for that course, I now routinely include “al-Tusi’s Derivative” alongside “Newton’s Derivative.” It is eye-opening to learn that a discovery relevant to calculus was made so long ago as the year 1209, by the Persian-born mathematician Sharaf al-Din al-Tusi in Baghdad. Also surprising is that his work was stimulated by a problem from ancient Greek geometry that Archimedes had studied but had been unable to solve. The problem was how to cut a given line segment of length \(a\) into two pieces such that the square of the first piece of length \(x\), times the second piece of length \(a-x\), equals a given volume \(c\). Al-Tusi’s predecessor Muhammad ibn Isa al-Mahani (Baghdad, c. 850) succeeded in converting this problem into an algebraic equation, \(x^3+c=ax^2\), and in the following century that equation was solved using conic sections. But al-Tusi took things even further, wondering how large the volume \(c\) can be and still admit of a solution; in modern terms, he was trying to maximize the polynomial function \(c=ax^2-x^3\). His search led him to the discovery that the relative maximum of a cubic polynomial can be located by finding the roots of a certain quadratic polynomial associated with it—in modern terms, derived from it (Houzel 1995; Katz 2009: 290-292).
In writing the module, "Using the Derivative to Solve an Optimization Problem," I devised a story that helps make the problem concrete and contemporary (see Figure 2):
Sami is a maintenance worker at a hospital in Baghdad. He has been asked to curtain off the area around a patient bed for privacy. The bed is in a corner of one ward, so the curtain needs to shield only two of its sides: there will be a square drape shielding one long side, and a smaller rectangular drape shielding the foot of the bed. Both lengths of curtain will drape from curtain rods suspended at equal heights from the ceiling of the hospital ward. But this is where Sami faces a problem. Because of war and supply shortages in Baghdad, the only material that he has available for the curtain rods is a 6-meter wooden pole, which he can cut into the two pieces that he needs. Sami is concerned to know how large a rectangular volume he will be able to enclose with these two pieces of curtain rod.
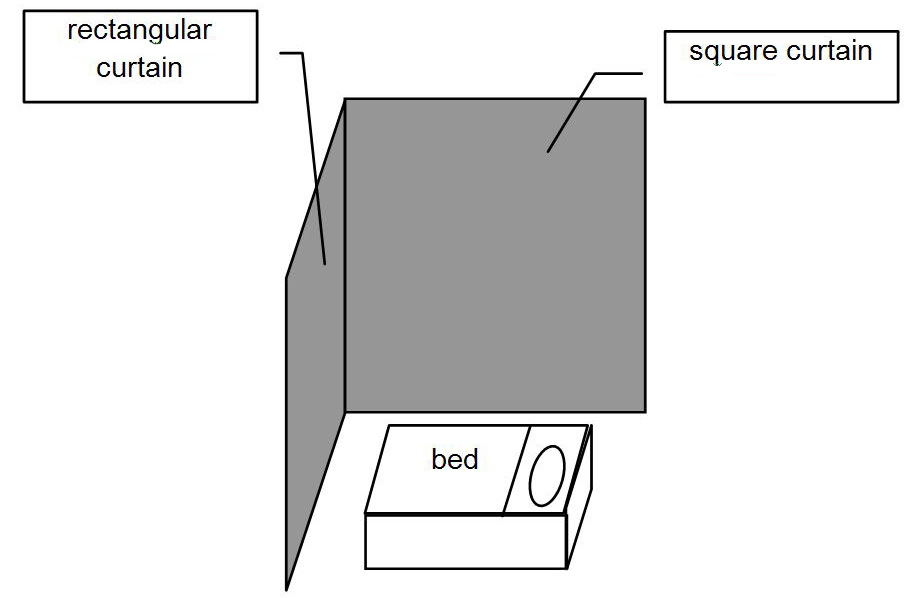

Figure 2. Al-Tusi’s discovery about cubic polynomials can be recast as a problem in optimizing a volume for hospital privacy.
I ask my students to convert this problem into a cubic equation, much as al-Mahani had done, and to examine the polynomial numerically, graphically, and analytically. The module guides them through the steps that al-Tusi is supposed to have taken (Farès 1995: 220-2), which are reminiscent of the development of a difference quotient. Eventually, we find that the maximum volume of privacy is 32 cubic meters, achieved by making the square curtain 4 meters by 4 meters, and the rectangular curtain 2 meters by 4 meters. Al-Tusi’s insight, and its use in resolving Sami’s dilemma, is the first example of optimization that my students encounter in this course.
- Download the module discussed on this page, Using the Derivative to Solve an Optimization Problem (Calculus for Business and Social Sciences).
- Download another module designed for my Calculus for Business and Social Sciences course, The Rule of Double False Position.