CalcPlot3D, an Exploration Environment for Multivariable Calculus - Contour Plots
Certain types of contour plots are not too difficult to create by hand. Many of these have contours that are lines, circles, or ellipses. But there are a lot of interesting functions whose contour plots are much more difficult to create by hand. I still require my students to be able to create contour plots of the first sort by hand, and they can certainly use the applet to visually verify their results. But I like to require them to use the applet to create contour plots for several functions whose contours are more complicated so they can improve their geometric intuition connecting the surface plots of various types of functions with their contour plots.
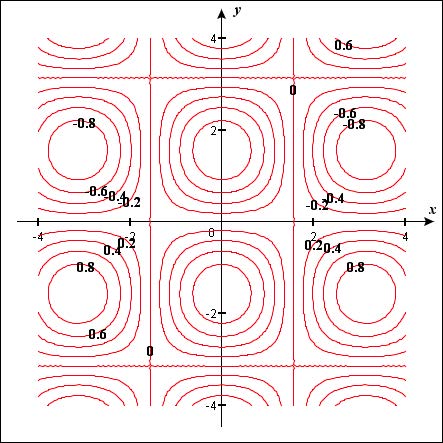
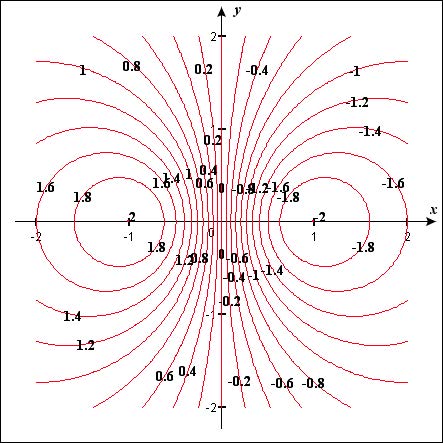
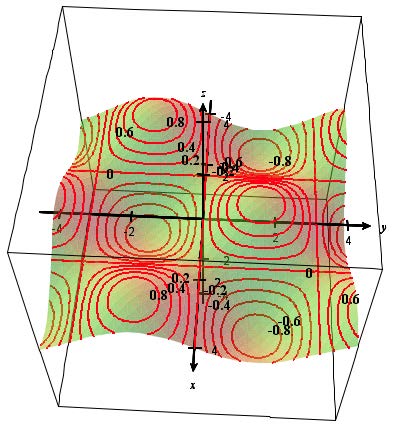
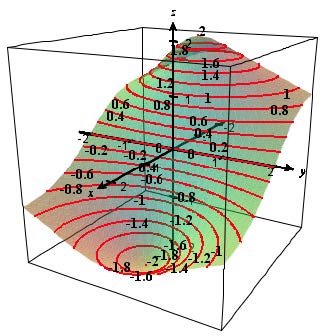
Exercise: Create contour plots for \(z = Cos(x)Sin(y)\) and \(z = -4x/(x^2+y^2+1) \). Print these contour plots and then for each one, click on the contour plot to see the contours as they appear on the surface. For each function, find a viewpoint that shows the surface and contours clearly and print this surface plot as well.
|
|
|
| \(z=Cos(x)Sin(y)\) | \(z=-4x/(x^2+y^2+1)\) |
To create these contour plots, you will start by entering the function in Function 1 and graphing it. Then select the Draw Contour Plot option from the Contour Plot menu. A dialog will appear. Be sure that Function 1 is selected on the left. For the first function, you will then enter -1 for the First Step, 0.2 for the Step Size and 11 for the Number of Contours. Then click on the OK button to see the contour plot appear.
If you click on the contour plot, you will the 3D surface plot of the function will be graphed along with the contours on the surface.
For the second function, you will do the same thing, except you can enter -2 for the First Step, and 21 for the Number of Steps.
 |
 |
Click here to open the CalcPlot3D applet in a new window.
Click here to open a pdf file which contains the instructions for the activity.