CalcPlot3D, an Exploration Environment for Multivariable Calculus - Directional Derivatives
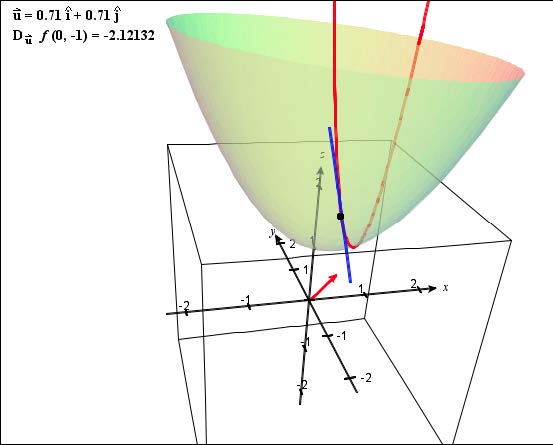 Exercise: Determine the directional derivative function for \( f(x, y) = x^2 + xy + y^2 + 1 \) in the direction of v = i + j. Then determine its value at the point (0, -1).
Exercise: Determine the directional derivative function for \( f(x, y) = x^2 + xy + y^2 + 1 \) in the direction of v = i + j. Then determine its value at the point (0, -1).
Use CalcPlot3D to graph this surface and show the appropriate tangent line on the surface at the point (0, -1) and displaying the unit direction vector and the correct directional derivative value.
To do this, first enter the function in Function 1. Then choose the directional derivative option from the drop-down menu just above the Trace Plot to the left of the 3D plot. You can then use the Trace Plot menu at the top of the applet to enter the point (0, -1) and the direction vector. I recommend hiding the edges (using the E key or the Hide Edges option on the View Settings menu) and also making the surface transparent
(using Ctrl-T or the Make Surfaces Transparent option on the View Settings menu). Rotate the plot until you can clearly see the direction vector, the surface, the tangent line, and the directional derivative value. Be sure it is the approximation of the exact value you obtained in your homework problem.
Click here to open the CalcPlot3D applet in a new window.
Click here to open a pdf file which contains the instructions for the activity.