To construct an Equilateral Triangle upon a given Line. Let AB be the given Line; Take this Line in the Compasses; set one foot in A and draw an Arch above the middle of the Line, and do the same from B … two lines drawn from A, B to the intersection of the Arches in C will be the equilateral Triangle ACB.

These lines come from the geometry copybook of a boy named Thomas Porcher. It’s about 6¹/₂ inches by 9¹/₂; it’s bound in green card. It has more than 200 pages, so it’s quite a chunky volume. Thomas wrote it around 1770.

Figure 1. Thomas Porcher constructs an equilateral triangle.

What was it like to learn geometry in Georgian England? It depended very much on who you were and what you were – and hence on why you were learning it in the first place. In this article we’ll look at two examples which show some of the differences between different approaches. But the two young men concerned had one thing in common, at least: they both prepared geometrical copy-books containing a record of what they learned and how they learned it, enabling us to reconstruct something of their geometrical education.

Thomas Porcher was about 14 at the time he wrote his copy-book; he was born in 1756 (the same year as Mozart). His book is a remarkable feat of penmanship: neat, meticulous, and accurate, it must have taken many long hours to do. Porcher’s was a fairly prosperous family, it seems, in Walworth, near London, England. We don’t know much about them, though one of Thomas’s sons, Samuel, would make good in the New World: by 1811 he owned a plantation in South Carolina, which he named Walworth after his family’s home in England. Porcher Avenue in Eutawville, South Carolina was named after the family.

Thomas was probably learning geometry with a tutor. This tidy book isn’t the kind of product that would normally have been created in a school setting, where a bit more chaos usually seems to have ruled.

Porcher’s book contained a very full course on geometry and measurement. The first half covered drawing lines, constructing plane figures, and inscribing and circumscribing figures around one another. It taught how to construct ‘proportional’ lines and a selection of other geometrical theorems such as this one.

To describe an Undecagon in a given circle.

Draw the semidiameter AB, divide it equally in two at G; from the points A and G with the same space describe the arches [arcs] GDI & AD; from I and the same space ID describe the Arch DO. The length GO will be an exact side of the Undecagon required.

Figure 2. Thomas Porcher constructs an undecagon.

This part culminated with Pythagoras’ theorem, and then the second half of the book turned to the art of measuring: measuring surfaces, measuring solids, and also plane trigonometry (that is, measuring triangles). Most of this was set out with quite abstract axioms, constructions and calculations, but towards the end there were some real-world problems: ‘To measure the Height of an accessible Tower’; ‘To measure the Distance of two places, neither of which is Accessible’; ‘To find the Diameter of the Earth from one observation’. But these, too, were exercises in trigonometry rather than practical surveying: once a few numbers had been put into the problem the rest was just calculation, using the methods set out earlier in the book. Sometimes there were explicit references to Euclidean theorems, which were invoked to justify certain steps in the calculation. The diameter of the earth was typical:

Let there be chosen a high hill AB near the sea shore, and let the observator [be] on the top of it, with in exact Quadrant divided into minutes and seconds by transverse Divisions, and fitted with a Telescope in place of the common sights …

The observer was to measure the angle between the horizon BE and the vertical AB, and the rest was then trigonometry – assuming the height of the hill was known – bringing in two Euclidean theorems concerning similar triangles.

Figure 3. Thomas Porcher’s Earth, with a high hill.

In this case the abstraction of the discussion was emphasised by the fact that no actual numbers were brought in: the outcome of the exercise was a method for finding the diameter of the earth, not the diameter itself. On the other hand, several of the problems did provide actual numbers, and thus helped Thomas Porcher practice not just Euclidean reasoning but also trigonometrical calculation.

To measure the Breadth of a river from one side only without going to the other side.
From A I observe an object at C where I want to measure the Breadth of the River from B. The Distance from B to A is 47.5 feet, and with the Quadrant I take the Angle at A to C and find it to be 36º54'. AB I make the Base, AC will be the Hypothenuse: and CD the perpendicular of a right-angled Triangle, right angled at B.

Simple trigonometry, relying on a printed set of tables, then made the breadth of the river 35.663 feet (with a rounding error in the third decimal place).

Figure 4. Thomas Porcher’s river.

Quite a lot of what was in Thomas Porcher’s book – particularly in its first half – was also to be found in Euclid’s Elements, that famous geometry textbook and one of the foundations of school and university geometry in the eighteenth century. Thomas Porcher’s book contained many propositions in a Euclidean style, and like Euclid’s Elements it began with definitions and axioms, some of them taken quite closely from the Greek master. Some of the propositions were based more or less closely on Euclid, too, like the construction of the equilateral triangle quoted above, or his version of Pythagoras:

In all right angled plain Triangles, the square of the longest side called the Hypothenuse, is equal to the sum of the squares of the 2 short legs.

But the structure of geometry had been completely re-thought compared with Euclid. Where did it come from? Not out of Porcher’s head, and probably not out of his teacher’s either. In places there are notes, now illegible, which might have recorded where the material came from. It’s quite possible that young Thomas copied his book from a teacher’s manuscript, or even from a printed book. But I think it’s more likely that he was drawing on more than one model, putting bits of them together and noting in the margin – sometimes – where the different sections came from.

What was the point of it all? What was the use of the huge labour of copying down two hundred pages of text and diagrams with such care, when there were perfectly good geometry textbooks in print, many of them at very reasonable prices?

You’ll probably know the famous story about the death of Archimedes: Archimedes was,

as fate would have it, intent upon working out some problem by a diagram, and having fixed his mind alike and his eyes upon the subject of his speculation, he never noticed the incursion of the Romans, nor that the city was taken. In this transport of study and contemplation, a soldier, unexpectedly coming up to him, commanded him to follow to Marcellus; which he declining to do before he had worked out his problem to a demonstration, the soldier, enraged, drew his sword and ran him through.

That account tells us, in a way, the same story as Thomas Porcher’s copy-book. Geometry was often thought of, in the ancient and the early modern worlds, as an absorbing discipline, involving both the mind and the hand and enabling the student to be indifferent to all kinds of distractions. It was often held up as a useful and an ennobling study for that very reason: by fixing the mind on higher, immaterial things it trained the student in proper methods of reasoning and taught a virtuous detachment from the distractions of everyday life. It could ‘charm the passions, restrain the impetuosity of imagination, and purge the Mind from error and prejudice’, ‘accustoming it to attention’, and ‘giving it a habit of close and demonstrative reasoning’, according to the Scot John Arbuthnot, whose essay on the ‘Usefulness of Mathematics’ was reprinted several times during the first half of the eighteenth century.

Those were reasons for teaching geometry to well-to-do students, whether in schools or universities (it was often lamented during the eighteenth century that geometry had fallen too much out of the university curriculum). They were reasons for studying geometry in the meticulous, deductive way Thomas Porcher did: if you wanted to beautify your mind and train yourself in proper habits of thought and reasoning.

But this was also the age of Newtonian science, and of rapidly increasing confidence about what mathematics could do in practical life. For an increasing range of trades it was vital to learn some mathematics: for some it had always been vital. Consider surveying, or navigation, the construction of sundials (‘dialling’) or the estimation of liquid volumes in barrels (‘gauging’). They all required a use and perhaps an understanding of geometrical ideas. And they were all rather far removed, both intellectually and socially, from the ideas about mental purity and abstraction we’ve just been talking about. It’s sometimes said that mathematical education split into two halves in Georgian Britain: deductive methods for the sons of gentlemen; practical rules for their social inferiors. Although there were exceptions, that pattern was particularly clear in the case of geometry, where there really were two different ways of learning the subject depending on why you were doing so.

A second example will show what I mean.

Robert Gardner compiled what he called his ‘Book of Accompts’ during the 1780s, in Lancashire. It covered a period in his mathematical education when he was doing some advanced arithmetic and also – despite the title – learning some geometry. It was a larger book than Thomas Porcher’s – nearly a foot tall, giving lots of room on the page for diagrams and illustrations – but a slimmer one: just fifty pages or so.

The geometrical parts were thoroughly practical in character.

To Measure Windows. Multiply the side of a Square by its Self or if a long Square the Length by the Bredth. Note 144 Sq. Inches makes a Square Foot, 9 Square Feet a Square Yard, and 42¹/₄ Square Yards make a Rood Westmoreland Measure.

(We’ll come back to that slightly surprising Westmoreland rood.)

Other topics were measuring pavements, measuring boards and boarded floors, and measuring land. There was a section, for instance, devoted to measuring trapezoidal pieces of land: presumably a response to the shape of local fields.

Suppose a Field in the form of the annexed Trapezea whose Diagonal Line is 468 yards the one perpendicular 110 yards the other Perpendicular 186 Yards. … Note you must multiply ¹/₂ the Diagonal into the sum of the two perpendiculars or ¹/₂ the sum of the two perpendiculars into the whole Diagonal for the Contents.

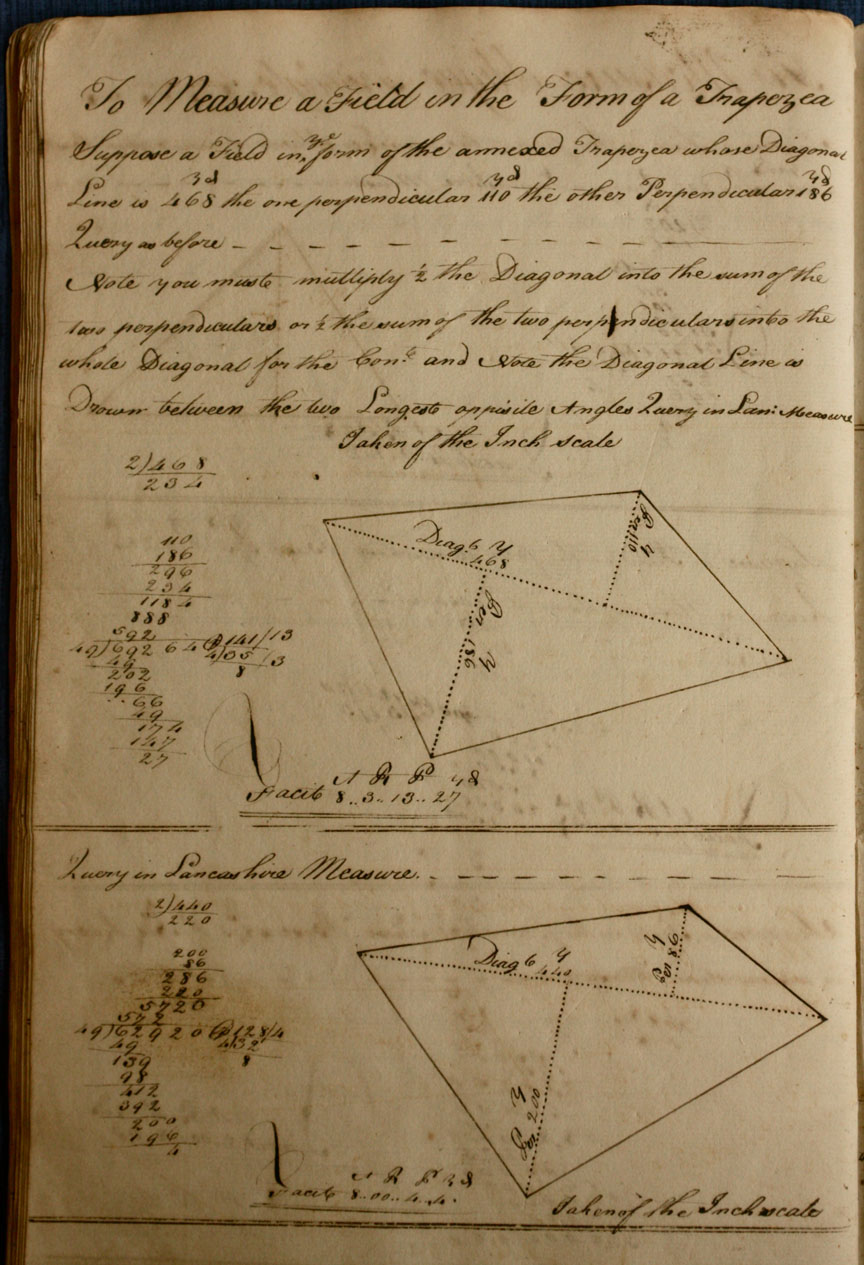
Figure 5. Robert Gardner’s trapezoidal field

In this case the sum of the perpendiculars was 296 yards and half the diagonal was 234; their product was 69,264 square yards. Gardner wrote out the working in full.

The geometric and trigonometrical problems to be solved were not always very far removed from what we saw in Thomas Porcher’s case. But Gardner solved his problems by pre-learned rules, and was unconcerned with such abstractions as theorems and proofs. His questions demanded not elegant methods but practicable answers, and space was given to such minutiae as the different systems of measurement one might come across:

7 Yards Square that is 49 yards make a Perch Lancashire Measure; Other Counties have a Different Number of Yards to their Pearch. As Westmoreland have 6¹/₂ Yards … to their Pearch that is 42¹/₄ or 42.25 Yards to their [square] Pearch. Statute or Yorkshire have 5¹/₂ Yards to their Pearch that is 30¹/₄ or 30.25 Yards to their [square] Pearch.

Figure 6. Robert Gardner measures ceilings and paintwork.

This was also a messy book, as the illustrations above show: one quite clearly aimed at learning practical techniques rather than anything else. Gardner might have been learning this material at a school or as part of a class of students with a tutor. It certainly doesn’t look as if anyone was paying very close attention to the appearance of his work on the page, and indeed the appearance really doesn’t seem to have been the point. If it was less neat and careful in some respects than Thomas Porcher’s book, Gardner’s nevertheless had a concern with correct methods and accurate results: but for very different reasons. Here was no desire to beautify the mind, but a part of a practical education for a tradesman. It’s an utterly different kind of book from Porcher’s: a practical tool rather than the record of a disciplined and beautiful mind.

An inscription in the middle of his book records that Gardner lived at Cockerham in Lancashire in 1787; he was quite probably the Robert Gardner who was baptized in that town in August 1765, making him 21 or 22 when most of the book was written. It looks very much as though he was learning mathematics as part of a practical education to get him into a particular trade: surveying or something closely related. The book itself would have served him as a practical tool, with correctly-worked examples covering a range of different plausible types of situation.

Suppose a Gable end to be measured. Breadth at the Bottom 19 feet 6 inches height to the Square 21 feet 9 inches height above the Square 15 feet 6 inches … NB you must multiply the height to the Square into the Bradth at or below the Square And for that above the Square Multiply the hight into the Breadth at or below the Square or ¹/₂ the Breadth into the height. Then add the Contents togather ….

These two books show how different geometry could appear – in every sense – from different parts of the social spectrum. Gardner would have gone on to one of the trades: quite likely a surveyor or something in the quantity-surveying line, given his book’s emphasis on calculating the sizes not just of fields but of walls, windows, roofs and floors. Porcher more likely lived a gentry life: we’ve no evidence that he was a gentleman of private means, but working in a trade or craft was quite probably not his destination. So one young man would have put his geometry to practical use, while the other used it as the foundation, perhaps, for further polishing of his mental faculties in reasoning and judgement.

Either way, geometry was an important part of an education that would shape the future course of a life, whether in the form of practical skills or mental discipline. And in both cases it left its traces – very different traces – in the form of copy-books laboriously put together over months or years, so that today we can find out, and see, something about what it meant to learn geometry in Georgian England.

Further Reading

For more about everyday mathematics in Georgian England see Benjamin Wardhaugh, Poor Robin’s Prophecies: A curious Almanac, and the everyday mathematics of Georgian Britain (Oxford, 2012). A sister article to this one is about to appear in Plus Magazine; it will discuss how arithmetic was learned in Georgian England. (Editor's note: Learning Arithmetic in Georgian England has since appeared in Plus Magazine, an online publication of Cambridge University devoted to "living mathematics.")

Thomas Porcher’s and Robert Gardner’s copy-books are in a private collection; namely, mine! You may use my photographs of the copy-books in this article in your classroom, but please contact me, Benjamin Wardhaugh, for permission to use them for any other purpose.

The quotes from John Arbuthnot are from his Essay on the Usefulness of Mathematical Learning (Oxford, 1701). There’s a great little book about English mathematical schoolbooks: John Dennis, Figuring it out: children’s arithmetical manuscripts 1680–1880 (Huxley Scientific Press, 2012); and for America there’s also Nerida Ellerton and Ken Clements, Rewriting the history of school mathematics in North America 1607–1861 (Springer, 2012).

About the Author

Benjamin Wardhaugh lives in Oxford, England. He trained in mathematics, music and history, and has taught both science to historians and history to mathematicians. He is a Fellow of Wolfson College, where he studies and writes about history, particularly its mathematical parts.