How to Calculate \(\pi\): Machin's Inverse Tangents, A Mini-Primary Source Project for Calculus 2 Students

 

Almost every mathematical culture through history seems to have proved, trusted, or suspected that the area of a circle is a fixed constant times the square of its radius. It is maybe not surprising, then, that the last two millennia have seen a seemingly endless array of attempts to calculate this constant (today usually called \(\pi\)) with increasing precision. Despite this history, actually calculating \(\pi\) is not a significant part of the standard undergraduate curriculum. (Try asking your senior mathematics majors to calculate \(\pi\) by hand from first principles, even to two decimal places. My own students are not always up to the challenge.)

   Calculation of \(\pi\) – Historical Record Holders. Wikipedia.

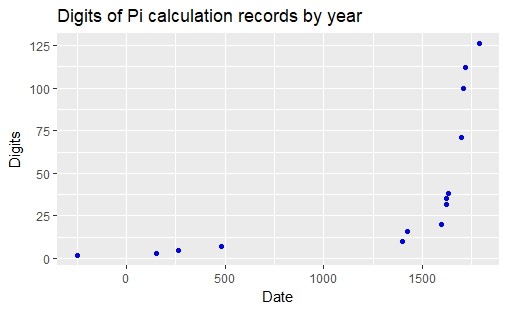
Name	Date	Number of Digits
Archimedes	250 BCE	2
Ptolemy	150	3
Liu Hui	263	5
Zu Chongzhi	480	7
Madhava of Sangamagrama	1400	10
Jamshīd al-Kāshī	1424	16
Ludoplh van Ceulen	1596	20
Ludoplh van Ceulen	1620	32
Willebrord Snell	1621	35
Christoph Grienberger	1630	38
Abraham Sharp	1699	71
John Machin	1706	100
Thomas Fantet de Lagny	1719	112
Jurij Vega	1789	126

A careful consideration of who has held the record for \(\pi\) calculation at any time is well beyond the scope of this introduction. I would like, however, to accept as a reasonable proxy the list of calculation records as it appears on Wikipedia on the day I write this. (The skeptical reader may like to know that the list is largely consistent with the list on MacTutor.)

It seems that people made progress fairly steadily for 2000 years, as incrementally more effort was spent and better notation was developed. Then, around 1700, progress in digit calculation accelerated noticeably.

How can we explain this noticeable increase in humanity’s ability to calculate \(\pi\)? It was not the result of simply spending more time and effort on the problem; rather the improvement was a result of a new technology—an understanding of the infinite series of arctangent! One of the first people to put this technology to work was John Machin (1680–1751), a long-time secretary of the British Royal Society.

Machin’s work is fascinating from a modern point of view, as it serves as a bridge between earlier geometric methods of calculating \(\pi\) and the analytic methods based on infinite series that would dominate in the following centuries.

It seems that no record of this work written by Machin himself has survived, but we do have an account of it written by the English judge Francis Maseres (1731–1824), also a Fellow of the Royal Society (Maseres 1796). As Maseres recounted the method, Machin realized he could use the formula for the tangent (or arctangent) of the difference of two angles to estimate a given fraction of \(\pi\), and thus of \(\pi\) itself. In order to do this, Machin needed to find an angle with two important properties:

• The tangent of the angle is a simple, easy-to-use small fraction; and

• Using the double-angle formula, one can use this angle to find the tangent of an angle very close to \(\pi\)/4.

As a bonus, it would be nice if plugging the fraction into Leibniz's series led to an easy-to-calculate value.

As some readers of Convergence know, Machin succeeded handsomely in this endeavor. Noting the convenient fact that, in Maseres' words, “the tangent of 1/4 of 45° is nearly = 1/5”, Machin not only knew that

\(\pi/4 ≈ 4 * \arctan(1/5)\),

but was able to use the difference-of-angles formula to find

\(\pi/4 = 4 * \arctan(1/5)\, – \arctan(1/239)\).

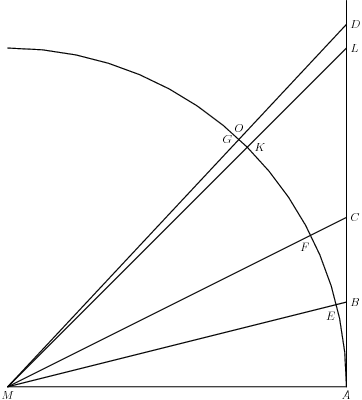
A good picture can reveal an entire argument. Segment AB = arctan(1/5), segment AC = 2arctan(1/5), and segment AD = 4arctan(1/5). Angle AMK = \(\pi\)/4, giving us immediately (if we trust the diagram) that \(\pi/4 ≈ 4 * \arctan(1/5)\).

In this Primary Source Project, students use Machin’s ideas about difference-of-tangent formulas and rapidly-converging series to gain an understanding of how \(\pi\) could be calculated. They also gain an appreciation of the relationship between geometric and analytic trigonometry, and can observe directly and numerically how quickly an infinite series (in this case, the Leibniz series for arctangent) converges.

The complete project How to Calculate π: Machin's Inverse Tangents (pdf file) is ready for student use, and the LaTeX source code is available from the author by request. A set of instructor notes that explain the purpose of the project and guide the instructor through the goals of each of the individual sections is appended at the end of the student project.

This project is the sixth in A Series of Mini-projects from TRIUMPHS: TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources appearing in Convergence, for use in courses ranging from first year calculus to analysis, number theory to topology, and more. Links to other mini-PSPs in the series appear below. An additional three mini-PSPs on methods for calculuating \(\pi\), based on works by Archimedes, Leonhard Euler, and the Compte de Buffon, are also planned for inclusion in the full TRIUMPHS collection. 

Acknowledgments

The development of the student project How to Calculate π: Machin's Inverse Tangents has been partially supported by the TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) project under Grants No. 1523494, 1523561, 1523747, 1523753, 1523898, 1524065, and 1524098. Any opinions, findings, and conclusions or recommendations expressed in this project are those of the author and do not necessarily reflect the views of the National Science Foundation.

References

Chronology of computation of \(\pi\). Wikipedia. Accessed August 3, 2018.

Maseres, Francis. 1796.  A most easy and expeditious method of squaring the circle, invented by the late Mr. John Machin, Professor of Astronomy in Gresham College, London, and Secretary to the Royal Society. Scriptores logarithmici; or a Collection of Several Curious Tracts on the Nature and Construction of Logarithms, Volume III, pp. 155–164. London: J. Davis.