There is some consensus in curricular guidelines, such as the National Council of Teachers of Mathematics (NCTM) Principles and Standards for School Mathematics [10], about the necessity of enhancing the human aspect of mathematics. As a human creation, mathematics is part of our everyday life and culture, and individuals are expected to understand and appreciate it. Better knowledge of how different ideas emerged throughout the history of mathematics, and to which problems or questions these ideas gave a solution, helps to reinforce the role of mathematics in everyday life and in science and other disciplines.

Interest in knowing how history of mathematics can be used to improve the instruction and the learning of mathematics is not new. Mathematics educator Michael Fried [6] gave the following reasons why educators should consider the history of mathematics:

1. History of mathematics humanizes mathematics. It offers an enriching multicultural approach, providing students historical role-models, and linking the study of mathematics with human emotions and motivations.
2. It makes mathematics more interesting, more comprehensible and more attainable, adding more variety to teaching, decreasing students' fear and rejection of mathematics, and reinforcing the role of mathematics in society.
3. History of mathematics gives a new perspective to concepts, problems and their solutions. From the point of view of students, history provides a context for problems and ideas, suggests alternative approaches to problem-solving, and shows the relationships between ideas, definitions, and applications.

With respect to the last item, the gaining of perspective is not limited only to students, since teachers and researchers also benefit from the study of history. The historical study of a particular mathematical concept can determine a method to make an epistemological analysis of it and to identify modern students' possible difficulties. According to Guy Brousseau [2], epistemological obstacles can be detected by comparing the history of mathematical topics and today's students' mistakes in learning them. In other words, mathematics education researchers should identify obstacles encountered during the history of mathematics and compare these historical obstacles with those faced by today's learners in order to determine their epistemological character ([2], p. 42).

There are several ways to incorporate history of mathematics into teaching practice, but they follow two basic strategies. On the one hand, a teacher may introduce historical anecdotes or specific historical problems; and on the other hand, she may use a determined historical development to explain a specific technique or idea and/or to organize subject contents according to a historical scheme [6].

Frank Swetz [13] suggested the importance of allowing students to take an active part in historical discoveries: to experiment with the measurement of \(\pi\), to employ Eratosthenes' technique to measure the circumference of the earth, to use Greek ruler and compass construction, and to experience approximations of the roots of algebraic equations. Reimer and Reimer also recommended that teachers integrate the history of mathematics in different ways [12], to include:

• reading aloud mathematical stories to the class;
• having students write about mathematical history topics;
• having students perform plays, enact stories, or make videos about historical topics;
• providing experiences with manipulatives; and
• providing mathematical experiences through the arts.

Powers and square roots are one of the topics in the arithmetic section in the final level of primary education in the Spanish curriculum. At the end of this educational stage, students must be able:

• to recognize the base and exponent of a power;
• to read, write, and calculate powers of numbers;
• to connect the square and square root of a given number;
• to compute the square roots of small numbers; and
• to solve problems involving squares and square roots.

The square root is defined as the inverse operation of the multiplication of two identical factors, with textbooks for this course usually reading that "the square root of a number is another number whose square is the given number". Students have no problem in determining that the square root of \(36\) is \(6,\) because \(6^2=36,\) or that the square root of \(81\) is \(9,\) since \(9^2=81.\) The square roots of small three-digit numbers, for example \(169,\) are found by looking for the number that was multiplied by itself to get \(169.\) In this way, the student makes successive attempts, \(11^2=121,\) \(12^2=144,\) and \(13^2=169,\) to conclude that the square root of \(169\) is \(13.\)

Teaching squares roots should comprise estimation skills together with certain intuitive and innovative components. As stated in the NCTM Principles and Standards [10],

When students can connect mathematical ideas, their understanding is deeper and more lasting. They can see mathematical connections in the rich interplay among mathematical topics, in contexts that relate mathematics to other subjects, and in their own interests and experience. Through instruction that emphasizes the interrelation of mathematical ideas, students not only learn mathematics, they also learn about the utility of mathematics.

When children build with, interact with, and handle manipulative materials, they can learn mathematical concepts through significant experiences that guarantee a deeper and better internalization of the processes and concepts on which they work. Godino, Batanero, and Font [7] consider as manipulative materials physical objects taken from the environment or specifically built for the purpose, as well as graphics, concrete words, sign systems, etc. acting as expressions, explorations, or a means of calculating in mathematical work. For these authors, manipulative materials bridge the real world with mathematical objects.

The aim of this paper is to describe an educational experience carried out with a group of students in the sixth and final grade of primary education (11-12 years old) and intended to promote the learning of a method for computing square roots. Being aware that the curricular treatment given to square roots in secondary education focuses on the algorithmic aspect, we intended to provide a more meaningful learning experience for these sixth-grade students. To this end, we introduced a historical method for computing square roots, and had students use manipulative tools to facilitate the interaction of geometric and arithmetic procedures required by this method. We believe we were successful in introducing what is a complex subject at this educational stage.

Square root extraction is an important topic treated in many ways throughout the history of mathematics. One of the most important ancient Chinese mathematical books, The Jiuzhang Suanshu (Nine Chapters on the Mathematical Art), compiled by several authors during the Han Dynasty (206 BCE – 220 CE), devotes Chapter 4, Shao guang (Short width), to problems about shortening the length of a field with increasing width but constant area. The method of finding square roots described there, Kai Fang (Method of Opening the Square), determines the square root by an iterative procedure based upon successive approximations by completing squares. Nevertheless, there are few occurrences of instructions describing the method followed to compute the square root of a number. The first detailed description of the procedure, reasoned with geometrical arguments, was given in the commentary on the Nine Chapters by Liu Hui in the third century CE. [3], [9]

Briefly speaking, Liu Hui's method for finding the square root proceeds by determining a whole number \(a\) whose square is less than or equal to the given area \(S\); that is, \(a^2\le S.\) If \(a^2=S,\) then \(a\) is the square root of \(S\), and we have finished. Otherwise, if \(a^2< S,\) then we take \(a\) as the first approximation of the square root of \(S\). Next, we obtain a whole number \(b\) such that \(a^2+2ab+b^2\le S.\) In this way, if \(a^2+2ab+b^2=S\), then \(a+b\) is the square root of \(S\) and the extraction is finished. But if \(a^2+2ab+b^2<S\), then the algorithm continues to find an integer value \(c\) for which \(a^2+2ab+b^2+2ac+2bc+c^2 \le S,\) and so on. If \(S\) is a perfect square, this process will eventually stop! Figure 1 depicts the case in which \(a^2+2ab+b^2+2ac+2bc+c^2 = S\) [3, p. 247]. In this case, the square root of \(S\) is \(\sqrt{S} =a+b+c\) and \(S\) itself is the square \[S={(a+b+c)}^2 = a^2+2ab+b^2+2ac+2bc+c^2.\]

Figure 1. Kai Fang for an integer \(S\) with \(S={(a+b+c)}^2\).

The example discussed by Liu Hui in his Problem 12 of Chapter 4 of the Nine Chapters consists of the calculation of the square root of \(55225\) [3, pp. 247-248]. First, let us think about the number of digits in the length of the side of a square with area \(55225.\) Since \[100^2 = 10000<55225<998001 =999^2,\] then \(55225\) (and every other five-digit whole number that is a perfect square) has as its square root an integer with three digits. For \(55225,\) let's call the square root \(abc\) with polynomial expression \(100a+10b+c.\) (Note that we have altered somewhat the scheme illustrated in Figure 1. Now, the side length of the yellow square is \(100a,\) of the red square is \(10b,\) and of the blue square is \(c,\) with the side length of the entire square \(100a+10b+c,\) or the three-digit integer \(abc.\))

We consider now the following decomposition of \(S=55225\): \[S=50000+5200+25.\] (Here, the number is divided into groups of two significant digits starting on the right.)

We first find the largest integer \(a\) whose square is less than or equal to \(5,\) and thus for which \((100a)^2\) is less than or equal to \(50000.\) If we take \(a=2,\) the area of the square of side \(100a=200\) (the yellow square in Figure 2) leaves as a remainder the area \(55225 - 40000 = 15225\). The latter is the area of the gnomon that remains when the yellow square is removed from Figure 2.

Next, following the geometrical argument by Liu Hui, this gnomon of area \(15225\) can be decomposed into two \(200\times (10b+c)\) rectangles of area \(200(10b+c)\) and a square of side length \(10b+c\) and area \((10b+c)^2\).

Figure 2. The first two (of three) steps in obtaining the square root of \(55225\).

Ignoring for now the value of \((10b+c)^2\), we seek \(b\) such that \[2\cdot 200\,(10b+c)\le 15225.\] Ignoring \(c\), this requires \[400\cdot 10b=4000b\le 15225.\] Since \(4000\cdot 3=12000<15225,\) but \(4000\cdot 4=16000>15225,\) we set \(b=3.\) With \(a=2\) and \(b=3\), the area of the gnomon is: \[2\cdot (100a)(10b+c) + (10b+c)^2 =12000+400c+900+60c+c^2 = 15225,\] so that \(c^2 + 460c = 2325.\) Since \(c=5\) satisfies this equation, we have determined that the square root of \(55225\) consists of digits \(a=2\), \(b=3\), and \(c=5\), and is \(abc=235\) (or \(100\cdot 2 + 10\cdot 3 +5 = 235).\)

Figure 3. The square root of \(55225\) is \(235.\)

In our classroom experience with sixth grade students, described in the next section, we worked with perfect-square three-digit integers, all of which have two-digit square roots. Therefore,  our scheme consisted of just the yellow and red parts of the diagrams above and we sought square roots of the form \(10a+b.\)

We introduced the historical method for computing square roots described in the preceding section, implemented with the help of manipulatives, to children in their last year of primary school during the 2017-2018 academic year. The participants were 67 sixth-grade primary education students (11-12 years old) in a public urban primary school in Granada (Spain). The students were divided into three groups of 22, 23, and 24 children. For each of the three groups, the experiment was held during a one-hour class session as part of the “Sciences Week Project” developed in the school.

The researcher brought to the classroom rectangles and squares of different colors and sizes made of EVA foam. Students would use these rectangles and squares to “open the square” of a given area. Students were provided with several squares of sizes 1x1, 2x2, 3x3, 4x4, ..., 10x10, and 20x20, as well as different rectangles of sizes 1x10, 2x10, 3x10, ..., 7x10, and 1x20, 2x20, 3x20, ..., 7x20 (all measures are in centimeters).

At the beginning of each session (one for each classroom group) the researcher asked the students what they knew about square roots. They recalled that “the square root of a number is the inverse operation of squaring that number” and that “the square root of a number is another number that when multiplied by itself will equal the initial number”.

Figure 4a. Kai Fang in the classroom: A group of students computes the square root of 196.

The researcher used, as a first example of the Kai Fang construction from the Nine Chapters, the computation of the square root of 144; some students knew the value of this square root. To illustrate the example, the researcher represented 144 as the area of a square on the blackboard. Inside this square, and sharing the same lower left vertex, she depicted a new square with sides of length 10. At this point, she explained to the students that the area not covered with this new square should be filled with two rectangles of the same size and a new square. These rectangles were placed, one above the square of area 100 and the other to its right, having a side in common with this square. This left a new square, smaller in size, at the upper right corner of the original square, to be covered. The side length of this new square was determined by the smallest side of the two rectangles; namely, 2. While the whole representation of the decomposition of the bigger square into two squares and two rectangles was performed, the decomposition of 144 as the sum of the corresponding areas was written on the blackboard.

As the researcher worked on the blackboard, the students reproduced the construction with the manipulative materials at their desks. Once the construction was completed, the length of the side of the square of area 144 was determined as the sum of the length of the largest side of the rectangles (and thus of the length of the square of area 100) and of the length of the side of the square with area equal to 4, yielding 10 + 2 = 12. The result was identified with the operations previously performed on the blackboard. When the students used the method and materials to compute the square roots of 169 and 225, they acknowledged the need to start with the largest possible square (the one of size 10 by 10), and then discussed which rectangles and which square they would need to complete their squares.

Next, the students started to work with the manipulative materials in groups of four. At the same time, the researcher reproduced on the blackboard the Kai Fang constructions of the square roots of 169 and 225, considering all the tries performed by some of the groups before getting the solution. As they worked, the students summoned the researcher or one of the two assistant teachers if they had any doubts, or to confirm that their answer was right.

Figure 4b. Kai Fang in the classroom: A group of students computes the square root of 486.

Next, we gave the students a questionnaire that asked them to obtain the square roots of four numbers:

(a) \(\sqrt{196},\)  (b) \(\sqrt{484},\)  (c) \(\sqrt{256},\)  and  (d) \(\sqrt{576}.\)

They were told to use the manipulative materials in order to, for each item, choose from among the different pieces those that they needed to complete the square with area equal to the number for which they must obtain the square root. The students were simultaneously

• completing the tasks with the manipulatives,
• transcribing the operations used for the decomposition, and
• drawing the geometric construction on a grid with numbered axes.

This information was filled in on a form provided for this purpose. We describe the children's results and our conclusions in the next sections of this article.

Operations performed by a student to calculate \(\sqrt{196}\).	Graphical representation of completing the square to get \(\sqrt{196}\).

Figure 5. Details of a student's graphical calculation of \(\sqrt{196}\).

As described in the preceding section, students were to implement a method from ancient China for computing the following square roots of three-digit integers:

(a) \(\sqrt{196},\)  (b) \(\sqrt{484},\)  (c) \(\sqrt{256},\)  and  (d) \(\sqrt{576}.\)

The students were to:

• use manipulatives (squares and rectangles) to construct a square with side length equal to the square root,
• transcribe the operations used for the decomposition, and
• draw the geometric construction on a grid with numbered axes.

Figures 5-7 on this page show samples of students' written work. Figures 4a and 4b on the preceding page show students' constructions with manipulatives. Table 1 summarizes students' performance.

Table 1. Absolute and relative (%) frequencies of students' resolutions (\(n\)=69):

Table 1 shows that, on average over the four examples, more than 92% of the students adequately drew the geometric representation of the construction using the Kai Fang method. However, around 35% of the students had difficulties adequately expressing the decomposition of the radicand as the sum of the areas of the figures used in the construction, item (d) being the one that gave them the greatest difficulty in this sense. For item (d), 40.58% of children did not perform well the decomposition of 576. This may be due to the fact that some students tried to decompose the radicands by means of only their hundreds, tens and units without considering the geometric distribution. Thus, while in sections (a) \(\sqrt{196}\) and (b) \(\sqrt{484}\) the figures of the hundreds, 1 and 4 (100 and 400), corresponded to perfect squares, the same did not happen with (c) \(\sqrt{256}\) and (d) \(\sqrt{576}\), for which 2 and 5 (200 and 500) required “completion”.

More specifically, students should have decomposed the numbers (a) \(196,\)  (b) \(484,\)  (c) \(256,\) and (d) \(576\) as follows:

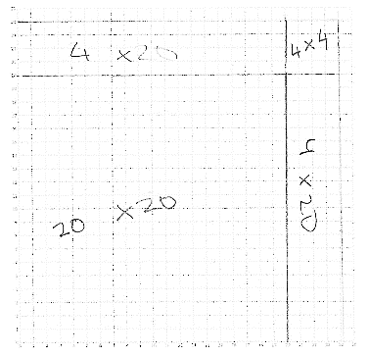
Figures 6 and 7 show student work on the trickier tasks (c) \(\sqrt{256}\) and (d) \(\sqrt{576}\):

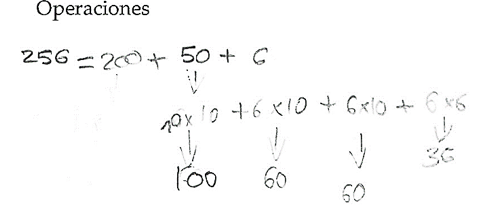Operations made by a student to get \(\sqrt{256}\).	A graphic representation of the completing of the square to get \(\sqrt{256}\).

Figure 6. Details of Kai Fang calculation for \(\sqrt{256}\).

Operations performed by a student to calculate \(\sqrt{576}\).	Graphical representation of completing the square in\(\sqrt{576}\).

Figure 7. Details of Kai Fang calculation of \(\sqrt{576}\).

As reported in Table 1, more than 84% of the students wrote correctly the result for all four of the requested roots. For most of the students who did not express the result of the calculation of the roots, the associated graphical representations were correct and we suspect a lapse in transcription. All 8 of those who did not write the result of \(\sqrt{196}\) performed the graphical representation correctly, and 3 of the 5 who did not write the result of \(\sqrt{484}\) did correctly decompose 484. Four of the 11 students who did not itemize the result for \(\sqrt{256}\) had properly performed the decomposition but made errors in the graphic representation. Finally, only 3 of the 8 students who did not write the result for \(\sqrt{576}\) did the graphic representation wrong.

Therefore, we can conclude that the types of errors detected are the following:

• When students express the result, they identify the decomposition of the radicand with the root, or they do not recognize the radical symbol and write that the root of the number is equal to the number itself.
• Arithmetic or expression errors; equalities are interwoven in the operations carried out to decompose the area.
• The decomposition does not correspond to the sum of the areas of the squares and rectangles.
• The student does not complete the square well.

These errors will be illustrated in the next section of this article.

In this work we have presented a classroom experience that exemplifies a feasible use of mathematics history in primary education. The didactical design introduces the students to the procedure known as Kai Fang for the calculation of the square root and is supported using manipulative materials. The method, used in ancient China, combines arithmetical and geometrical practices in such a way that it provides a wider network of meanings for the mathematical objects put into play than those of the usual algorithm. Therefore, our experience supports the line of thought of other authors [5], who claim that both teachers and students need to learn that mathematics is much more than the isolated knowledge of a series of calculation procedures. Along these lines, the history of mathematics can serve as an instrument to expand this reductionist view and to influence attitudes and beliefs about mathematics.

As noted in the preceding section, the types of student errors we detected are as follows:

• When students express the result, they identify the decomposition of the radicand with the root (see Figure 8a), or they do not recognize the radical symbol and write that the root of the number is equal to the number itself.
• Arithmetic or expression errors; equalities are interwoven in the operations carried out to decompose the area.
• The decomposition does not correspond to the sum of the areas of the squares and rectangles (see Figure 8b).
• The student does not complete the square well (see Figure 9).

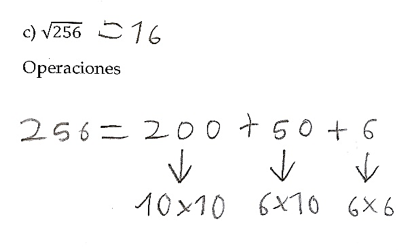a) Mistake when expressing the root of\(\sqrt{196}\).	b) Radicand decomposition does not match the sum of the areas in the calculation of \(\sqrt{256}\).

Figure 8. Arithmetical mistakes.

It is clear from the results that the students use different additive decompositions on their way to finding the perfect square and the requested root. Although it would be necessary to have a larger sample of participants and a greater diversity of numbers on which to calculate their roots to know for sure, the results in Table 1 indicate that, in our case, students had no more difficulties in breaking down the number 576 compared to 196.

The student fails to decompose the square to calculate \(\sqrt{196}\).	The student fails to decompose the square to calculate \(\sqrt{256}\).

Figure 9. Geometrical mistakes.

The time devoted to the activity was short: the explanation, examples and resolution all were done in one hour. Even with this short time, the results were satisfactory from the cognitive and affective points of view and strengthen our interest in tasks of this typology. It would be interesting to be able to devote more sessions to reinforce or remember the Kai Fang technique, even for the computation of non-exact square roots, by means of new rectangles.

It should be noted that the required physical manipulation to graphically represent the arithmetic expressions as areas of flat figures (squares and rectangles in this case) enriches the didactic sequence. Duval [4] points out the need to consider changes of semiotic system in the tasks to be carried out and the knowledge to be developed by the students, because in this process one gains in understanding about the mathematical object in question.

The work developed in the decompositions involves a sequence of contextualized arithmetical expressions, which also allows students to deepen their understanding of the equals sign "as a symbol of mathematical equivalence" [8]. This aspect is often neglected in primary education and therefore it is frequently identified as a source of difficulties when passing from arithmetic thinking to algebraic thinking. In addition, the proposed task previews work with polynomial identities in secondary education, providing a series of physical actions that can later be evoked to facilitate, for example, the identification of the square of a sum.

Furthermore, we consider this task to be amenable to and enhanced by the use of a virtual manipulative, performed, for example, with GeoGebra. The procedures the students used are illustrated by the two applets are provided at the start of this article. We repeat these applets below.

The first applet allows users to compute two-digit integer square roots (from 10 to 99) of integers between 100 and 9801.

The second applet allows users to compute three-digit and some four-digit square roots.

References

[1] Avital, S. History of Mathematics Can Help Improve Instruction and Learning, in F. Swetz, J. Fauvel, O. Bekken, B. Johansson, and V. Katz (eds.), Learn from the Masters, The Mathematical Association of America, Washington, 1995: 3-12.

[2] Brousseau, G. Les obstacles epistemologiques et la didactique des mathematiques, in N. Bednarz and C. Garnier (eds.), Construction des savoirs Obstacles et Conflits, CIRADE Les éditions Agence d'ARC Inc., Quebec, 1989: 41-63.

[3]  Dauben, J. W. Chinese Mathematics, in V. Katz (ed.), The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook, Princeton University Press, 2007: 187-384.

[4] Duval, R. Representation, Vision and Visualization: Cognitive Functions in Mathematical Thinking. Basic Issues for Learning, in Proceedings of the Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, 1999.

[5] Fauvel, J. and van Maanen, J. (eds.) History in Mathematics Education: The ICMI Study, New ICMI Study Series, vol. 6. Kluwer, Dordrecht, 2000.

[6] Fried, M. Can Mathematics Education and History of Mathematics Coexist? Science and Education, 2001; 10: 391-408.

[7] Godino, J. D., Batanero, C., and Font, V. Fundamentos de la enseñanza y el aprendizaje de las matemáticas. In J. D. Godino, Didáctica de las matemáticas para maestros, Granada, 2004.

[8] Knuth, E. J., Stephens, A. C., McNeil, N. M., and Alibali, M. W. Does understanding the equal sign matter? Evidence from solving equations. Journal for Research in Mathematics Education, 2006: 297-312.

[9]  Li Yan and Du Shiran (trans. Crossley, J. N., and Lun, A. W.-C.), Chinese Mathematics: A Concise History, Oxford University Press, 1987.

[10] National Council of Teachers of Mathematics. Principles and Standards for School Mathematics, NCTM, Reston, VA, 2000.

[11] Po-Hung, L. Do teachers need to incorporate the history of mathematics in their teaching? The Mathematics Teacher, 2001; 96(6): 416-421.

[12] Reimer, W. and Reimer, L. Historical connections in mathematics: Resources for using history of mathematics in the classroom, AIMS Education Foundation, Fresno, CA, 1995.

[13] Swetz, F. J. Learning Activities from the History of Mathematics, J. Weston Walch, Portland, ME, 1994.

About the Authors

María Burgos (ResearcherID: L-5265-2014, MR Author ID: 803300) is currently an assistant professor in the Department of Didactics of Mathematics at the University of Granada, Spain. She has a PhD in Mathematics and a Master's degree in Didactics of Mathematics. Her main research areas are functional analysis, mathematics education, instructional design, and teacher training.

Pablo Beltrán-Pellicer (ResearcherID: K-2196-2017) is an assistant professor in the Area of Didactics of Mathematics at the University of Zaragoza, Spain, and a secondary education teacher. He has a PhD in Didactics, and his research interests are analysis and design of educational sequences, use of specific resources (audiovisual, technological, etc.), and theory of mathematics education.

Acknowledgements

The first author is partially supported by FQM126 Research Group (Junta de Andalucía, Spain). The second author is supported by MINECO EDU2016-74848-P and S36-17D Research Group in Mathematics Education (Government of Aragón, European Social Fund). The authors would like to thank the students and teachers who made possible this rewarding experience. They would also like to acknowledge P. A. García-Sánchez and J. D. Godino for their valuable comments and suggestions, and Janet Beery for her support in the reviewing process.