Numbers, magnitudes, and the place of algebra

Arabic arithmeticians (ḥussāb) calculated with any positive quantity that can be obtained from the unit through addition, subtraction, multiplication, division, and root extraction. Although they had no qualms about working with fractions and irrational roots, zero remained merely a placeholder in the base ten system of writing numbers, and we have no evidence that any medieval arithmetician considered the possibility of negative numbers.

Books on calculation (ḥisāb) taught methods of operating on known numbers, and many of them also explained techniques for finding unknown numbers. A typical sample problem for known numbers is this one from Ibn al-Yāsamīn's late twelfth-century Grafting of Opinions of the Work on Dust Figures (see Note 3, below):

If [someone] said to you, divide ten and a fourth by eight and a third. [Ibn al-Yāsamīn 1993, 172.5]

After working it out, the answer is found to be "one and two tenths and three tenths of a tenth". And a simple problem of finding an unknown number, from the same book, is:

If [someone] said to you, a quantity: you added its third and its fourth and got six. How much is the quantity? [Ibn al-Yāsamīn 1993, 195.9]

Here the answer is found to be "ten and two sevenths".

Today algebra is just about the only method taught for finding unknown numbers, but in medieval Islamicate countries several methods were practiced. Ibn al-Yāsamīn, in fact, solves the problem given above by four different methods: single false position, algebra, al-qiyās (see Note 4, below), and double false position. Like the other methods, algebra was a numerical technique, and was regarded as being part of arithmetic. So where I write about "Arabic arithmetic" keep in mind that it includes algebra. I will describe this algebra below, in the section "Arabic algebra".

And as in Greek mathematics, geometry and arithmetic were distinct domains. The objects of geometry were magnitudes: points, line segments, triangles, spheres, etc. Although magnitudes were regarded as being of a fundamentally different nature from numbers and independent of them, people fostered the connection between geometrical and arithmetical calculation by routinely assigning numerical measures to magnitudes.

Geometric vs. arithmetical proofs

People who have had only a little exposure to medieval Arabic algebra will often recall one or two names, usually al-Khwārizmī (ca. 825 CE) and al-Khayyām (Omar Khayyam, ca. 1075). People also tend to recall that these authors gave geometric proofs to the rules for solving simplified equations. Indeed, the proofs in the algebra books of many other authors are also based in geometric diagrams. Abū Kāmil (late 9th c.), Thābit ibn Qurra (late 9th c.), al-Karajī (early 11th c.), al-Samawʾal (12th c.), and Sharaf al-Dīn al-Ṭūsī (d. 1213) are the most well-known. But even the few people who have studied Arabic algebra in some depth can be excused for not knowing that it is just as common for the proofs of these rules to be based in arithmetic. The secondary literature has for the most part neglected the two sets of arithmetical proofs in two works of al-Karajī, as well as the arithmetical proofs in later authors like Ibn al-Yāsamīn (d. 1204), Ibn al-Bannāʾ (late 13th c.), al-Fārisī (late 13th c.), and Ibn al-Hāʾim (1387). (See Note 5, below.)

Al-Karajī had proven the rules for solving three-term quadratic equations via geometric diagrams with the appropriate references to Euclid's propositions II.5 and II.6 in his [Book of] al-Fakhrī on the Art of Algebra (henceforth al-Fakhrī). It was later, in his short treatise Causes of Calculation in Algebra and in his finger-reckoning book The Sufficient [Book] on Arithmetic, that he switched to arithmetical proofs. [See Note 6, below.] The other authors listed above were inspired directly or indirectly by him, though their proofs are by and large very different from each other.

Authors eschewed geometry in favor of arithmetic for different reasons. Al-Fārisī, for his part, held that because algebra belongs to arithmetic, proofs in algebra should properly be conducted arithmetically. This way Aristotle's prohibition of genus-crossing would be observed [Posterior Analytics Book I, part 7]. One should not prove results in the genus of arithmetic, like the rules for solving equations, by arguments in the genus of geometry. Al-Karajī and Ibn al-Hāʾim, on the other hand, both explained that proofs based in Euclid's Elements are simply too difficult for students learning algebra. Al-Karajī wrote in his short treatise Causes of Calculation his reason for moving away from the proofs based in geometry that he had previously given in al-Fakhrī:

… Then I saw that people seeking knowledge of calculation found it difficult to understand the correctness [of the rules] by means of those lines and figures, given their understanding by means of the tongue and hand. I discovered that many people found it very difficult when reading [the proofs] in books. And I decided because of this to make the proofs in this book easier. [Saidan 1986, 354.8]

Thus he switched to proofs based in arithmetic, which "puts an end to the incomprehensibility of the realm of lines and figures".

---

Note 3. The Arabic title of the book Grafting of Opinions of the Work on Dust Figures is Talqīḥ al-afkār fī l-ʿilm bi-rushūm al-ghubār. All translations in this article are by the author.

Note 4. Al-qiyās can be translated as "scaling". It consists of undoing the operations on the unknown, and works only for simple problems.

Note 5. I have recently published a paper outlining their arithmetical proofs, in [Oaks 2018].

Note 6. The Arabic titles of the three books [Book of] al-Fakhrī on the Art of Algebra, Causes of Calculation in Algebra, and The Sufficient [Book] on Arithmetic, are, respectively, al-Fakhrī fī ṣināʿat al-jabr wa-l-muqābala, ʿIlal ḥisāb al-jabr wa-l-muqābala, and al-Kāfī fī l-ḥisāb. These are published in [Saidan 1986, 95-351], [Saidan 1986, 353-369], and [al-Karajī 1986], respectively.

Finger reckoning

Al-Karajī's "people seeking knowledge of calculation" practiced what we call finger-reckoning. In Arabic this method was known by various names, including "hand arithmetic", "open arithmetic", "aerial arithmetic", and "arithmetic of the Romans (i.e. Byzantines) and Arabs". (See Note 7, below.) Calculations were done mentally in base ten, and intermediate results were stored by positioning the fingers in particular ways. For example, Abū l-Wafāʾ (10th c.) explains that to multiply 46 by 28, one first finds 40 by 20 and 40 by 8, which together are 1120. This number is held on the fingers. Then the 6 is multiplied by 20 and by 8 to get 168, which is then added to the held 1120 to get the answer 1288. [Saidan 1971, 142.17] In the scheme described by ʿAlī ibn al-Maghribī in a fifteenth-century poem, units were stored by positioning the last three fingers on the right hand, tens with the right-hand thumb and index finger, hundreds with the left hand thumb and index finger, and thousands with the last three fingers on the left hand [Saidan 1968]. I know of no illustration from an Arabic source showing the positions of the fingers, but Luca Pacioli's famous Summa de Arithmetica has this nice engraving:

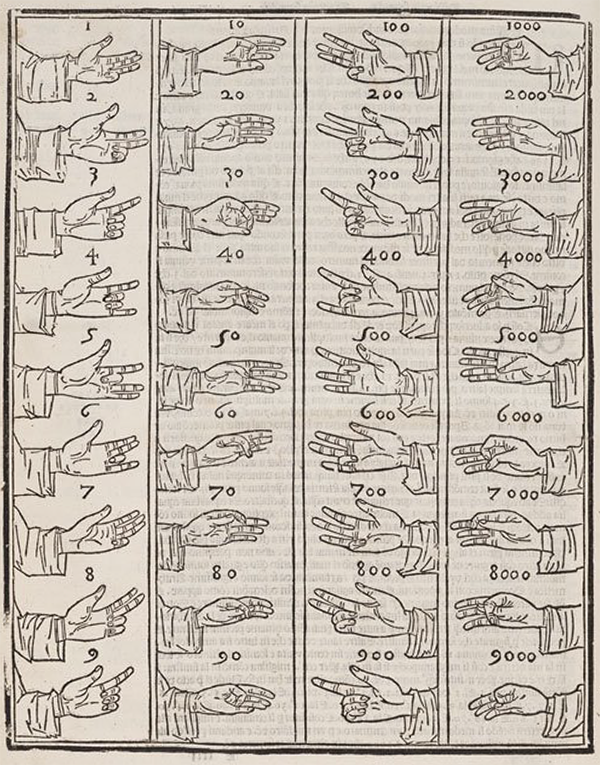
Figure 1. Finger positions in Luca Pacioli's 1494 Summa de Arithmetica. For additional images from Pacioli's Summa, see the Convergence article, "Mathematical Treasures - Pacioli's Summa".

In addition to laying out the steps for operating on whole numbers and fractions, books on finger reckoning present many shortcuts for particular situations. To multiply by 5 it is generally easier to take half and then multiply by 10, and there are similar shortcuts for multiplying or dividing by 25, 33\(1\over 3\), 125, etc. Or to multiply by 37 one can multiply a third of the number by 1, 10, and 100, and then add the results. One particular finger-reckoning rule for multiplying two numbers interests us for the unexpected use Ibn al-Bannāʾ made of it for proofs in algebra. This "squaring" rule is presented in many books, including Ibn al-Bannāʾ's own late thirteenth century Condensed [Book] on the Operations of Arithmetic (henceforth Condensed Book; see Note 8, below):

Another type is known as squaring. You take half of the sum of the two numbers and you square it. You subtract from the result a square of half of the difference between them. The remainder is the result of the multiplication. [Ibn al-Bannāʾ 1969, 51.7].

Ibn al-Bannāʾ gave no example to illustrate the rule, so I translate one from another book, the Completion of Arithmetic of al-Baghdādī (d. 1038):

For example, we want to multiply sixteen by twenty-four. We add them and we take half of the sum, which is twenty. We multiply it by itself, and we hold the outcome [with our fingers], which is four hundred. Then we take the difference between the two numbers to get eight. We multiply its half, which is four, by itself, to get sixteen. We subtract it from the four hundred that we held, leaving three hundred eighty-four, which is the required outcome. [al-Baghdādī 1985, 168.23]

We can express the rule algebraically as \(\left({1\over 2}(p+q)\right)^2-\left({1\over 2}|p-q|\right)^2=pq,\) but the application in finger-reckoning is somehow simpler, especially if the numbers are close together and half of their sum is easy to square. (Here and later I write \(|p-q|\) for the difference between two numbers. There was no concept of absolute value in medieval arithmetic because negative numbers were not acknowledged.)

Finger-reckoning was preferred by various professional groups, including government secretaries, merchants, and surveyors. One advantage of the method is that no writing was required. All calculations were worked out mentally with assistance from the fingers, and the results were expressed verbally. This is what al-Karajī meant by his phrase "by means of tongue and hand". Judging by the contents of books devoted to this kind of reckoning, practitioners would have often learned basic mensuration, but Euclid would have been out of reach.

---

Note 7. In Arabic, the names "hand arithmetic", "open arithmetic", "aerial arithmetic", and "arithmetic of the Romans and Arabs" are, respectively, ḥisāb al-yadd, ḥisāb al-maftūḥ, ḥisāb al-hawāʾī, and ḥisāb al-rūm wa-l-ʿarab.

Note 8. The Arabic title of the Condensed [Book] on the Operations of Arithmetic is Talkhīṣ aʿmāl al-ḥisāb. Incidentally, Ibn al-Bannāʾ copied this and some other rules word-for-word from Ibn al-Yāsamīn's Grafting of Opinions, without citing his source. Although plagiarism was frowned upon in Ibn al-Bannāʾ's time, it was not the crime then that it is now.

Ibn al-Bannāʾ

Abū l-ʿAbbās Aḥmad ibn Muḥammad ibn ʿUthmān al-Azdī al-Marrākushī is better known to us by the moniker Ibn al-Bannāʾ, which means "son of the builder". He lived his entire life in Morocco, from his birth in 1256 to his death in 1321. Ibn al-Bannāʾ was one of those brilliant medieval polymaths who wrote on a wide range of topics. He is known to have authored over a hundred works on mathematics, astronomy, logic, religion, law, language, philosophy, medicine, and the occult sciences. And like any good medieval polymath, Ibn al-Bannāʾ wrote textbooks in addition to more advanced works.

One of Ibn al-Bannāʾ's textbooks is titled Book on the Fundamentals and Preliminaries in Algebra (see Note 9, below). Like al-Karajī's al-Fakhrī, this book was written in the tradition of al-Khwārizmī and Abū Kāmil. But unlike those authors, Ibn al-Bannāʾ proves the rules for solving simplified equations in the setting of arithmetic rather than geometry. His approach was to complete the square in the context of the equation in each case, resting his arguments on the rule for squaring a binomial. For example, for the sample equation \(x^2+10x=39\) he adds 25 (the square of half of the 10) to both sides to get \(x^2+10x+25=64\), and he takes the square root of both sides to get \(x+5=8\), from which the solution falls out immediately. The steps in this process correspond to the steps in the rule, so the rule is proven. As befitting a textbook, these proofs are straightforward and easy to understand, which is why they are not the topic of this article.

Ibn al-Bannāʾ's Condensed Book from which I quoted above is another textbook, and in its time a very popular one. It is organized into two parts. In the first part he explains how to calculate with Indian (i.e. Arabic) numerals, and in the second part he covers the basic rules for solving problems by proportion, double false position, and algebra. He does not teach finger-reckoning in this book, but he does borrow some of the shortcuts from that system that might be useful for Indian calculation, including the "squaring" rule.

The Condensed Book is just too condensed to include proofs. It is so compact that even if Ibn al-Bannāʾ's main goal was to explain how to perform arithmetical operations, he did not include a single numerical example to illustrate the rules! To remedy this, he was the first among many to write a commentary on his little book that elaborates on the rules with examples, philosophical discussions, and proofs.

Ibn al-Bannāʾ completed his commentary in 1301, and gave it the title Lifting the Veil from the Face of the Operations of Arithmetic. (See Note 10, below.) But where the Condensed Book was a textbook on practical arithmetic for students learning to calculate with Indian numerals, many parts of Lifting the Veil were written for a more sophisticated reader. Ibn al-Bannāʾ engaged in philosophical investigations of the nature of number, the unit, and fractions, and many of his proofs were written at a level beyond the reach of arithmetic students.

It is in this book that Ibn al-Bannāʾ gave two more sets of proofs for the rules for solving simplified equations. These two sets are different from the proofs in his algebra book. The first set rests on the "squaring" rule from finger-reckoning, while the second set is based in arithmetical restatements of Euclid's propositions II.5 and II.6. And just as Euclid's propositions are removed from their geometrical context and redressed for a new purpose in algebra, the "squaring" rule is modified from its original form in finger-reckoning in preparation for the same purpose.

Arabic algebra

I cannot proceed any further without actually saying what these simplified equations are, so a brief overview of Arabic algebra is in order. Unlike algebra today, which encompasses any method of finding unknown numbers and even various kinds of formal, abstract reasoning, Arabic algebra (al-jabr wa-l-muqābala) was a specific technique of numerical problem-solving. It was characterized by its own technical vocabulary and procedures, and was practiced alongside other methods like single and double false position. Although algebra in Arabic was initially associated with the professional groups who practiced finger-reckoning, by Ibn al-Bannāʾ's time it had also become integrated into books on calculation with Indian numerals.

The powers of the unknown in Arabic algebra are given individual names. The first power is called a "root" (jidhr) or "thing" (shayʾ), and plays the role of our \(x\). Its square is called a māl, a word meaning "sum of money", "wealth", or "fund", and corresponds to our \(x^2\). Because the word māl was used in algebra in a sense unrelated to its quotidian meaning, and because there is no good English word corresponding to it, I leave it untranslated. I also write its plural with the English suffix: māls. Higher degree terms first appear in Abū Kāmil's Book on Algebra and in Qusṭā ibn Lūqā's translation of the Arithmetica of Diophantus, both from the latter ninth century. The cube of the "thing" is a "cube" (kaʿb), and higher powers were usually expressed as some combination of māl and kaʿb, like kaʿb kaʿb māl for the eighth power. Units were often counted in dirhams, a silver coin, but also frequently as "units" or "in number".

Equations were formed from these names. For example, Abū Kāmil sets up this equation to solve one of his problems:

[F]our ninths of a māl and four dirhams less two things and a third of a thing equal a thing and twenty-four dirhams. [Abū Kāmil 2012, 379.14]

Converting this into modern notation gives \[{4\over 9}x^2+4-2{1\over 3}x=x+24.\] Keep in mind that there is no negative quantity here. The "less" indicates that the positive \(2{1\over 3}x\) has been removed from the greater \({4\over 9}x^2+4\). Also, although books show the calculations in words, they were not worked out rhetorically. Calculations were performed mentally or in notation on some temporary surface like a dust-board. When needed, rhetorical versions were composed to communicate it to others in a book. Books were treated as transcriptions of lectures, and notation plays no role when listening to a teacher's recitation. Thus the lack of notation in books.

One way that equations differ from other forms of equating in Arabic mathematics is that they are stated using only these names. A simple example of an arithmetical equating that was not considered to be an algebraic equation is the enunciation to problem (I.17) in al-Karajī's al-Fakhrī:

Ten: you divided it into two parts, so the difference between them is equal (mithl) to the smaller part. [Saidan 1986, 173.15]

This question is framed in terms of the two unnamed parts of ten, and not with any algebraic name. We can restate it in algebraic terms by calling the parts \(x\) and \(10-x\) and setting up the equation \((10-x)-x=x\), but the enunciation as it stands belongs to arithmetic generally, and can be solved by methods other than algebra.

There is another way that equations are distinguished from other forms of equating. Several different words were used to mean "equal" in Arabic arithmetic, the most common being mithl, sawiya, and the prefix ka-, as well as the implied verb "to be". Algebraic equations, on the other hand, were always stated with the unusual verb ʿadala ("equal", "well-balanced"). This word was rarely used in mathematics outside the context of algebra. Noting which word Ibn al-Bannāʾ chooses to equate numbers and expressions will tell us how he understood his arguments.

---

Note 9. In Arabic, the title of Ibn al-Bannāʾ's Book on the Fundamentals and Preliminaries in Algebra is Kitāb al-uṣūl wa l-muqaddimāt fī l-jabr wa-l-muqābala. It is included in [Saidan 1986, 505-613].

Note 10. In Arabic, the title of Ibn al-Bannāʾ's Lifting the Veil from the Face of the Operations of Arithmetic is Rafʿ al-ḥijāb ʿan wujūh aʿmāl al-ḥisāb. It is available as [Ibn al-Bannāʾ 1994].

Solving the simplified equations

Just as in modern algebra, medieval equations were simplified to standard forms. Where we have one type of simplified quadratic equation, \(ax^2+bx+c=0\), Arabic algebraists classified six types. This is because the rules for solving them call for operations on their "numbers" (coefficients), and only positive numbers were acknowledged in premodern mathematics. So there were three simple, two-term equations which we write as

(1) \(ax^2=bx\),

(2) \(ax^2=c\), and

(3) \(bx=c\),

and three composite, three-term equations corresponding to our

(4) \(ax^2+bx=c\),

(5) \(ax^2+c=bx\), and

(6) \(bx+c=ax^2\)

Abū Kāmil simplifies his equation translated above as

four ninths of a māl and four dirhams less two things and a third of a thing equal a thing and twenty-four dirhams [Abū Kāmil 2012, 379.14]

to

twenty dirhams and three things and a third of a thing equal four ninths of a māl,

which we would write as \[20+3{1\over 3}x={4\over 9}x^2.\] This is a type 6 equation.

Each of the six types was solved by its own rule. Solutions to the simple equations are trivial, requiring at most a single division to find the root or the māl. The rules for the composite equations, however, are more complex. Here are Ibn al-Bannāʾ's solutions to the three composite types from his Condensed Book. First he gives the solutions presuming that the number (coefficient) of the māl is 1, and after that he explains that this number must be set to one before following the procedure:

To work out the fourth type you halve the number of roots and you square the half, and you add it to the number and you take a root of the result and you subtract the half from it, leaving the root.

The sixth type is solved similarly, except that you add the half at the end to a root of the sum to get the root.

For the fifth type, you subtract the number from a square of half of the number of roots, and you take a root of the remainder. If you add it to the half, it gives a root of the greater [māl], and if you subtract it, it gives a root of the smaller māl. Whenever a square of the half is equal to the number, then the half is the root, and the māl is the number.

For each of the three composite types, whenever there is more than one māl, reduce it to one māl, and likewise reduce all the terms in the equation. And for each of them, whenever there is less than one māl, restore it to one māl, and likewise restore all the terms in the equation. [Ibn al-Bannāʾ 1969, 75.1].

If these rhetorical instructions are not clear enough, we can contort them into modern notation. There is always one positive solution to the type 4 equation \(x^2+bx=c\), which is \[x=\sqrt{c+\left({b\over 2}\right)^2}-{b\over 2}.\] The one positive solution to the type 6 equation \(x^2=bx+c\) is \[x=\sqrt{c+\left({b\over 2}\right)^2}+{b\over 2}.\] The type 5 equation \(x^2+c=bx\) might have two, one, or no positive solutions. If \(\left({b\over 2}\right)^2>c\) then the two solutions are \[x={b\over 2}\pm\sqrt{\left({b\over 2}\right)^2-c}.\] If \(\left({b\over 2}\right)^2=c\) then there is only one solution, \(x={b\over 2}\), and \(x^2=c\). Ibn al-Bannāʾ remarks in his algebra book that if the discriminant is negative then there is no solution, but he says nothing about that here. And last, if the number of māls is not one, set it to one. For the type 4 equation \(ax^2+bx=c\), for example, one should work with the normalized version \[x^2+{b\over a}x={c\over a}.\]

Returning to Abū Kāmil's equation \[20+3{1\over 3}x={4\over 9}x^2,\] the \({4\over 9}x^2\) must first be restored to a full \(x^2\). He multiplies all terms by \(2{1\over 4}\) to get

forty-five dirhams and eight things and a fourth of a thing equal a māl' \(\left(45+8{1\over 4}x=x^2\right).\)

If he had bothered to spell out the subsequent steps, he would have shown us that we should take half of the \(8{1\over 4}\) to get \(4{1\over 8}\). Its square is \(17{1\over 64}\), and adding this to 45 gives \(62{1\over 64}\). Its square root is \(7{7\over 8}\), to which we add the \(4{1\over 8}\) to get 12, which is the value of the thing/root. Instead, he simply writes

You work it out the way I described to you to get twelve, which is the [unknown] quantity. [Abū Kāmil 2012, 379.20].

Because it is not apparent that these rules actually give the required values, many authors provided proofs that they work. The proofs in earlier books are based in geometry, while it is common for later proofs to be based in arithmetic.

Figure 2. Folio 51b from the Library of Congress manuscript of Lifting the Veil. The proofs begin on the 14th line, last word on the left. For an image of the title page of this work, see the Convergence article "Mathematical Treasure: Ibn al-Banna's Operations of Calculation".

Ibn al-Banna's proofs based in the 'squaring' rule

In Lifting the Veil, Ibn al-Bannāʾ follows the order of the contents of his Condensed Book. The "squaring" rule is given in the chapter on multiplication, and in his commentary he gives two modifications of this rule, together with a third rule to go with them. These are stated in precisely the forms that will be applied in his proofs later in the book:

The first type of the types of multiplication, known as "squaring", deems it necessary that the surface of two numbers with a square of half of the difference between them be equal (mithl) to a square of half of their sum. And if one of them is multiplied by the other and is subtracted from a square of half of their sum, it leaves a square of half of the difference between them. And a square of half of the difference between them is clearly a square of the difference between one of them and half of their sum. [Ibn al-Bannāʾ 1994, 260.5]

The "surface" (saṭḥ) of two numbers is their product (see Note 11, below). In modern notation, Ibn al-Bannāʾ's rules are:

(1) \(pq+\left({\frac{1}{2}}|p-q|\right)^2 = \left({\frac{1}{2}}(p+q)\right)^2\)

(2) \(\left({\frac{1}{2}}(p+q)\right)^2 - pq = \left({\frac{1}{2}}|p-q|\right)^2\)

(3) \(\left({\frac{1}{2}}|p-q|\right)^2 = {\left|{\frac{1}{2}}s-p\right|}^2,\) where \(s\) is \(p+q\).

The "squaring" rule had already been removed from the context of finger-reckoning in the Condensed Book, and here it is even further alienated from its origin, both because of the ways it is rearranged, and because Lifting the Veil is a book beyond the interests and abilities of the majority of secretaries and merchants learning practical arithmetic.

Rule (1) will be used for the proofs of the type 4 and 6 equations, while rules (2) and (3) will be used for the proof of type 5. Incidentally, rule (3) serves to convert rule (2) into the arithmetical version of Euclid's Elements proposition II.5, though Ibn al-Bannāʾ does not mention the connection with Euclid.

Note that these rules do not belong to algebra, but to arithmetic generally. We should already suspect this because they appear in the chapter on multiplication, before Ibn al-Bannāʾ introduces algebra. But there are other critical indications, the most obvious being that no unknown or undetermined number in these rules is given a name. Numbers are instead referred to by words and phrases like "one of them" and "the difference between them". For my notational versions I took the step of introducing algebra by naming the two numbers \(p\) and \(q\) and then constructing compound expressions from them. There is nothing of that in the Arabic. Additionally, none of these rules is written with the algebraic verb ʿadala ("equal").

Later, in the chapter on algebra, Ibn al-Bannāʾ gives his two sets of proofs. One feature of these proofs that sets them apart from the proofs in other authors is that instead of explaining one path toward obtaining the root or thing, he shows how the rule and the equation give rise to two simple equations, one of them type 1 (\(ax^2=bx\)) and the other type 3 (\(bx = c\)).

Ibn al-Bannāʾ runs through his arguments in general, without reference to particular equations. His directions are terse, so when Ibn al-Hāʾim reproduced them in his 1387 Commentary on the Poem of al-Yāsamīn he also worked them out in terms of sample equations. (See Note 12, below.) I will do the same, and with the same examples. Ibn al-Bannāʾ begins his proofs (see Note 13, below):

You can understand the cause (ʿilla) of the procedures for the composite types from the multiplication by "squares" that we mentioned before. You always make the two multiplied numbers the number and the māl.

Unlike the proofs in his algebra book, the arguments here take place in the context of one of the arithmetical rules. In each of the three proofs the two numbers of the rule (my \(p\) and \(q\)) will be the number (the constant term) and the māl, and the equation serves only to make substitutions. The operations called for in the rules are worked out, and the resulting expressions are then "confronted" to form new equations.

For the type 4 proof, Ibn al-Hāʾim and I follow Ibn al-Bannāʾ's steps for the standard example dating back to al-Khwārizmī: "a māl and ten roots equal thirty-nine", or in modern notation, \(x^2+10x=39\). Unlike the rules, the equation is stated in terms of a named unknown (the "thing") and with the verb ʿadala. Ibn al-Bannāʾ will work in the context of rule (1), and in our example the two numbers are 39 and \(x^2\). It does not matter which is which.

Then the difference between them is the things in the fourth type.

Their difference is \(39-x^2,\) which according our type 4 equation is "ten things", or \(10x\).

You multiply one of them by the other, giving māls \(\left[39x^2\right],\) and you add to them a square of half of their difference, giving māls [adding \(25x^2\) gives \(64x^2\)]. This is a square of half of their sum. You take its root, giving half of their sum, which are things \(\left[8x\right].\) So keep it in mind.

We have now calculated \(pq+\left({\frac{1}{2}}|p-q|\right)^2\) as \(64x^2\), whose square root is \(8x\). By rule (1) this should be equal to \({\frac{1}{2}}(p+q)\), which he now calculates:

Then you direct your attention to half of their sum to get a māl and half of the things which are with it, since the number is equal to the māl and the things. Adding the māl gives two māls and the things, and half of that is a māl and half of the things.

Adding an \(x^2\) to both sides of \(x^2+10x=39\) gives \(2x^2+10x=x^2+39\), which is their sum. So half of the sum is also half of the left side, which is \(x^2+5x\). He has now computed the two parts of the rule as algebraic expressions, and with them he sets up equations:

Confront it with the remembered amount, leaving things equal a māl, which is the first type.

A common way to express the setting-up of an equation from two algebraic expressions was to "confront" (qabila) them. By this act the equation \(x^2+5x=8x\) is established, which simplifies to the type 1 equation \(x^2=3x\). Solutions to simple equations are transparent, so there is no need to explain them.

And if you want, add half of the things to the remembered amount, to get things equal the number, and that is the third type.

Adding \(5x\) to both \(x^2+5x\) and \(8x\) results in \(x^2+10x\) and \(13x\), and from the original equation we know that the first of these is 39. So one confronts them to set up the type 3 equation \(39=13x\).

Ibn al-Bannāʾ next proves the rule for the type 6 equation, also using rule (1). I explain it in terms of Ibn al-Hāʾim's example \(x^2=3x+4\). Here the two numbers of the rule are 4 and \(x^2\). Again, it does not matter which is which.

Work out the sixth type similarly, except that half of their sum is all of the number and half of the things which are with it.

Adding 4 to both sides of the equation gives \(x^2+4=3x+8\), so \({\frac{1}{2}}(x^2+4)\) is \(4+{1\over 2}(3x)\).

This is equal (mithl) to the things resulting from the remembered root.

Since the product of the numbers is \(4x^2\) and the square of half their difference is \(\left({1\over 2}(3x)\right)^2\) or \(2{1\over 4}x^2\), their sum is \(6{1\over 4}x^2\). The "remembered root'' is then \(\sqrt{6{1\over 4}x^2}\), or \(2{1\over 2}x\). So \(4+{1\over 2}(3x)\) is equal to \(2{1\over 2}x\). By the particular word used for "equal" (mithl) we know that this is not intended as an algebraic equation, but is an equality still in the realm of the arithmetical rule.

So if you add half of the things to what you remembered from the things, your result is the first type.

Adding \(1{1\over 2}x\) to both, substituting \(x^2\) for the \(4+3x\), and confronting the two parts gives the type 1 equation \(x^2=4x\).

And if you subtract half of the things from the remembered [root], you get the third type.

Subtracting \(1{1\over 2}x\) from both gives the type 3 equation \(x=4\).

The type 5 equation is solved a little differently. I follow Ibn al-Hāʾim by explaining it in terms of the equation \(x^2+21=10x\). Now the two numbers are 21 and \(x^2\), though this time it will make a difference which is which.

And in the fifth type a square of half of the things is a square of half of the sum of the numbers.

In \(x^2+21=10x\) the square of half of \(10x\) is the square of \({1\over 2}(x^2+21)\). This is \(25x^2\).

You subtract from it the product of one of them by the other \(\left[21x^2\right],\) leaving a square of the difference between one of them and half of their sum.

Subtracting \(21x^2\) from \(25x^2\) leaves \(4x^2\), which by rule (2) is \(\left({1\over 2}|p-q|\right)^2\). But by rule (3) this is equal to \(\left|{1\over 2}s-p\right|^2\). So \(4x^2\) is \(\left|{1\over 2}s-p\right|^2\). Because \(p\) can be either \(x^2\) or 21, \(4x^2\) is either \(|5x-x^2|^2\) or \(|5x-21|^2\). And because we do not know which of \({1\over 2}s\) (\(5x\)) or \(p\) (21 or \(x^2\)) is greater, \(\sqrt{4x^2}\) might be \(x^2-5x\), \(21-5x\), \(5x-x^2\), or \(5x-21\). He considers the four cases in order:

If you take its root to get things \(\left[2x\right],\) and you add it to half of their sum, which is half of the things which are in the equation \(\left[5x\right],\) and you equate that with the māl, it results in the first type \(\left[7x=x^2\right].\) And if you equate it with the number [21] it gives the third type \(\left[7x=21\right].\)

And if you subtract [from the \(5x\)] a root of half of their remembered sum \(\left[2x\right]\) and you equate it with the māl, it likewise results in the first type \(\left[3x=x^2\right].\) And if you equate it with the number it results in the third type \(\left[3x=21\right].\)

In all four cases the word "equate" is conjugated from ʿadala, the particular verb used in algebraic equations. This act sets up the type 1 and 3 equations (written above in square brackets).

One might wonder how it is that these arguments were supposed to prove the rules for solving the three composite equations. The proofs read more like derivations of alternative methods, and no attempt is made by Ibn al-Bannāʾ to link his calculations with the different steps of the rules. We do know that he intended these to be proofs from his use of the word "cause" (ʿilla) in the beginning. This is the same word al-Khwārizmī and others used in their proofs. Based on other proofs in works of Thābit ibn Qurra and al-Karajī, my guess is that our author was just being exceptionally concise. The rules can be derived from these arguments—it just takes some work, just as it is not easy to decipher his line of reasoning without following along with sample equations.

---

Note 11. Use of the term "surface" (saṭḥ) for the product of two numbers is borrowed from Greek number theory, specifically from definition 16 from Book VII of Euclid's Elements. Heath translates the Greek term as "plane".

Note 12. Ibn al-Hāʾim's book is titled Sharḥ al-urjūza al-Yāsmīnīyya, and is published in [Ibn al-Hāʾim 2003]. He explains Ibn al-Bannāʾ's proofs beginning on page 83.

Note 13. Ibn al-Bannāʾ's Arabic text begins at [Ibn al-Bannāʾ 1994, 309.14]. In what follows for types 4 and 5, I copy from [Oaks 2018], with some minor adjustments.

Reading the language more closely

I have already explained two ways that equations in algebra can be differentiated from the equating of numbers in arithmetic. Equations are stated in terms of the names of the powers ("thing"/"root", "māl", "cube", etc.), and the two sides are always equated with the verb ʿadala.

There is another important way that arithmetical problems and rules, like the "squaring" rule, will differ from algebraic equations. I will illustrate this by comparing the finger-reckoning rule with Abū Kāmil's equation. Recall the rule:

You take half of the sum of the two numbers and you square it. You subtract from the result a square of half of the difference between them. The remainder is the result of the multiplication.

The equation is:

twenty dirhams and three things and a third of a thing equal four ninths of a māl.

Recall, also, that I rewrote both with modern algebraic notation, the rule as \(\left({1\over 2}(p+q)\right)^2-\left({1\over 2}|p-q|\right)^2=pq\) and the equation as \(20+3{1\over 3}x={4\over 9}x^2\).

We have already seen that the numbers in the rule are not expressed with algebraic names from which we could build composite expressions through operations. Here the numbers are only referred to as "the two numbers" and "them". I converted the rule into an algebraic identity by naming the numbers \(p\) and \(q\) and forming expressions from them. For instructors of mathematics this act of naming is second nature. To pick a simpler example, we can translate "the sum of two consecutive squares" into \(n^2+(n+1)^2\) with hardly a thought, but to many of our students this is a formidable task.

There is still another, perhaps more critical, difference between the rule and the equation, one that lies at the heart of what differentiates medieval from modern algebra. The rule, you will notice, is presented as a sequence of operations to be performed, with a specified outcome. One is instructed to take half of a sum, to square it, and to subtract another amount also obtained through a halving and a squaring, and the result of these operations is the product of the two numbers. The equation, by contrast, asserts the equivalence of two fixed amounts.

Let's examine the equation more closely. The expression "twenty dirhams and three things and a third of a thing" exhibits no operations at all. It is simply a collection of two kinds of object, \(20\) of one and \(3{\frac{1}{3}}\) of the other. It is like saying "twenty pounds and three and a third ounces". The expression does not call for the operation of addition, but instead indicates the aggregation of the two kinds with the common conjunction "and" (wa). Similarly, the "less" (illā) in expressions like "ten less a thing" (our \(10-x\)) is not the operation of subtraction, but is the negative counterpart to "and". It indicates that the ten is deficient, lacking a "thing".

There is no scalar multiplication in the equation, either. It would be just as silly to say that there is scalar multiplication in "three things and a third of a thing" as it would be to say that there is scalar multiplication in the expression "three and a third ounces". Likewise, the "four ninths of a māl" is spoken much like "four ninths of a kilogram" (to stick with units of weight/mass).

The two sides of an Arabic equation ideally contain no operations at all. (Exceptions were sometimes made for division, but there is no space to go into that here!) One can, of course, perform operations on algebraic expressions. For instance, we can multiply a thing by ten less a thing to get ten things less a māl. It is the individual expressions themselves that lack operations.

It is for this reason that Arabic algebraists insisted on working out all operations prior to setting up their equations. The two sides of the equation should be specified amounts, without any unresolved operations. Where our \[{4\over 9}x^2+4-2{1\over 3}x=x+24\] is built from the operations of addition, subtraction, scalar multiplication, and exponentiation, both sides of its medieval counterpart are aggregations of different kinds of number. Thus modern notation is not only inadequate for expressing medieval arithmetical rules, it also does not reliably express medieval algebraic equations!

I mention all this because it helps us better understand the unfolding of Ibn al-Bannāʾ's proofs. For each proof he has two pieces to work with: the rule and the equation. All the work takes place in the context of the rule, and he uses the equation only to substitute values. For his type 4 proof he cannot start off by stating some rhetorical equivalent of \[39x^2+\left({\frac{1}{2}}(39-x^2)\right)^2 = \left({\frac{1}{2}}(39-x^2)\right)^2\] and then work through the operations. Such a monstrosity could have been formulated, but it violates the idea of a "composite number" (polynomial) in Arabic. Instead, he must perform the operations first, and only when all additions, subtractions, and multiplications have been completed can he confront the two parts to form new, and simple, equations.

Note. For detailed studies on the ideas briefly outlined in this section, see [Oaks 2009] for the "aggregations interpretation" and [Oaks 2010] on the verb ʿadala.

Just who would have read these proofs?

I mentioned above that al-Karajī and Ibn al-Hāʾim both wrote proofs for finger-reckoners, the people al-Karajī described as "understanding by means of the tongue and hand." Ibn al-Bannāʾ's proofs based on completing the square in his algebra book would have been accessible to that crowd, too. Ironically, his proofs based in a rule originating in finger-reckoning were not meant for finger-reckoners. In Ibn al-Bannāʾ's hands the "squaring" rule migrated from a practical way of mentally multiplying numbers to the foundation for novel proofs in algebra. Like the high-level arithmetic books of other authors like Ibn Munʿim (12th-13th c.) and al-Fārisī, Ibn al-Bannāʾ's Lifting the Veil was intended for a more theoretically-minded readership.

In medieval Islam there was recurrent interplay between the different practical and theoretical traditions in mathematics. To pick three examples,

• al-Khayyām adapted practical algebra for use in Greek-style geometrical problem-solving,
• al-Fārisī gave the rules of finger-reckoning, including the "squaring" rule, a foundation in proofs modeled on those in Euclid's Elements Books VII-IX, and
• an anonymous ninth-century text, probably written by al-Māhānī, applied algebra to find numerically the roots of the binomials and apotomes described in Book X of Euclid's Elements.

Ibn al-Bannāʾ's Lifting the Veil is another example of this merging of the mathematics originating in different contexts.

About the Author

Jeffrey Oaks received his Ph.D. in mathematics from the University of Rochester in 1991, and he has taught mathematics at the University of Indianapolis since 1992. He began the study of history of mathematics in 1999, and has since published many studies in history of algebra, particularly in medieval Arabic algebra.

References

Abū Kāmil, 2012. Algèbre et Analyse Diophantienne. Edited and translated by Roshdi Rashed. Berlin: De Gruyter. This book gives the Arabic text with a French translation. There is an English translation of the fifteenth century Hebrew translation of this book in [Levey 1966].

Aristotle, n.d. Posterior Analytics, translated by G. R. G. Mure. Available online: http://classics.mit.edu/Aristotle/posterior.html

al-Baghdādī, 1985. Kitāb al-takmila fīʾl-ḥisāb. Edited by A. S. Saidan. Kuwait: Maʿhad al-Makhṭūṭāt al-ʿArabiyaḥ. Contains the Arabic text.

Ibn al-Bannāʾ, 1969. Talkhīṣ aʿmāl al-ḥisāb. Texte établi, annoté et traduit par Mohamed Souissi. Tunis: Université de Tunis. Contains the Arabic text with a French translation.

Ibn al-Bannāʾ, 1994. Rafʿ al-ḥijāb ʿan wujūh aʿmāl al-ḥisāb. Edited by Muḥammad Aballagh. Fās: Jāmiʿat Sīdī Muḥammad ibn ʿAbd Allāh, 1994. Contains the Arabic text.

Ibn al-Hāʾim, 2003. Sharh al-urjūza al-Yāsmīnīya, de Ibn al-Hāʾim. Edited and translated by Mahdi Abdeljaouad. Tunis: Publication de l'Association Tunisienne des Sciences Mathématiques. Contains the Arabic text and a partial French translation.

Ibn al-Yāsamīn, 1993. Muʾallafāt Ibn al-Yāsamīn al-riyāḍiyya [Mathematical Writings of Ibn al-Yāsamīn]. Edited by T. Zemouli. M.Sc. thesis in History of Mathematics, Algiers, E. N. S.

al-Karajī, 1986. al-Kāfī fī l-ḥisāb. Edited by Sami Chalhoub. Aleppo: Aleppo University. Contains the Arabic text.

Levey, Martin (Ed.), 1966. The Algebra of Abū Kāmil: Kitāb fī al-jābr waʾl-muqābala in a Commentary by Mordecai Finzi. Hebrew text, translation and commentary with special reference to the Arabic text. Madison: University of Wisconsin.

Oaks, Jeffrey A., 2009. "Polynomials and equations in Arabic algebra". Archive for History of Exact Sciences 63, 169-203.

Oaks, Jeffrey A., 2010. "Equations and equating in Arabic mathematics". Archives Internationales d'Histoire des Sciences 60, 265-298.

Oaks, Jeffrey A. 2018, "Arithmetical proofs in Arabic algebra". Pp. 215-238 in: Ezzaim Laabid, ed., Actes du 12^é Colloque Maghrébin sur l'Histoire des Mathématiques Arabes: Marrakech 26 au 28 mai 2016. Marrakech: École Normale Supérieure. Also available at the author's website: https://www.uindy.edu/cas/mathematics/oaks/files/oaksmarrakech.pdf

Saidan, A. S. 1968, "Finger reckoning in an Arabic poem". The Mathematics Teacher 61, 707-708.

Saidan, A. S, 1971. Tārīkh ʿilm al-ḥisāb al-ʿArabī. ʿAmman: Jamʿiyat ʿUmāl al-Maṭābiʿ al-Taʿāwinīa. Contains the Arabic text of Abūl-Wafāʾ's Kitāb Fīmā yaḥtāju ilayhi al-kuttāb wa-l-ʿummāl wa ghayruhum min ʿilm al-ḥisāb (Book of What is Necessary for Scribes, Dealers, and Others from the Science of Arithmetic).

Saidan, A. S, 1986. Tārīkh ʿilm al-jabr fī l-ʿālam al-ʿArabī. Kuwait: al-Majlis al-Waṭanī lil-Thaqāfah waʿl-Funūn wa-l-Ādāb, Qism al-Turāth al-ʿArabī. Contains the Arabic text of three works on algebra:

• al-Karajī's al-Fakhrī fī ṣināʿat al-jabr wa-l-muqābala ([Book of] al-Fakhrī on the Art of Algebra),
• Ibn Badr's Kitāb fīhi ikhtiṣār al-jabr wa-l-muqābala (Brief Book on Algebra), and
• Ibn al-Bannāʾ's Kitāb al-uṣūl wa-l-muqaddimāt fī l-jabr wa-l-muqābala (Book on the Fundamentals and Preliminaries in Algebra).