John Napier's Binary Chessboard Calculator - Division
How to divide one positive integer (the dividend) by another, smaller positive integer (the divisor), obtaining a non-negative integer quotient and a non-negative integer remainder:
Step 1. Represent the dividend in the horizontal margin and the divisor in the vertical margin.
Step 2. Place a counter on the largest number in the first column (farthest column to the right) that when multiplied by the divisor is less than or equal to the dividend.
Step 3. Multiply that number by the divisor and subtract the product from the dividend. Replace the dividend (in the horizontal margin) with this result, which will become the current dividend.
Step 4. Repeat steps 2 and 3 with the current dividend until you can no longer do so.
Step 5. The sum of the chips in the first column is the quotient. The current dividend is the remainder.
Example: That \(100\) divided by \(7\) results in a quotient of \(14\) and a remainder of \(2\) is illustrated below.
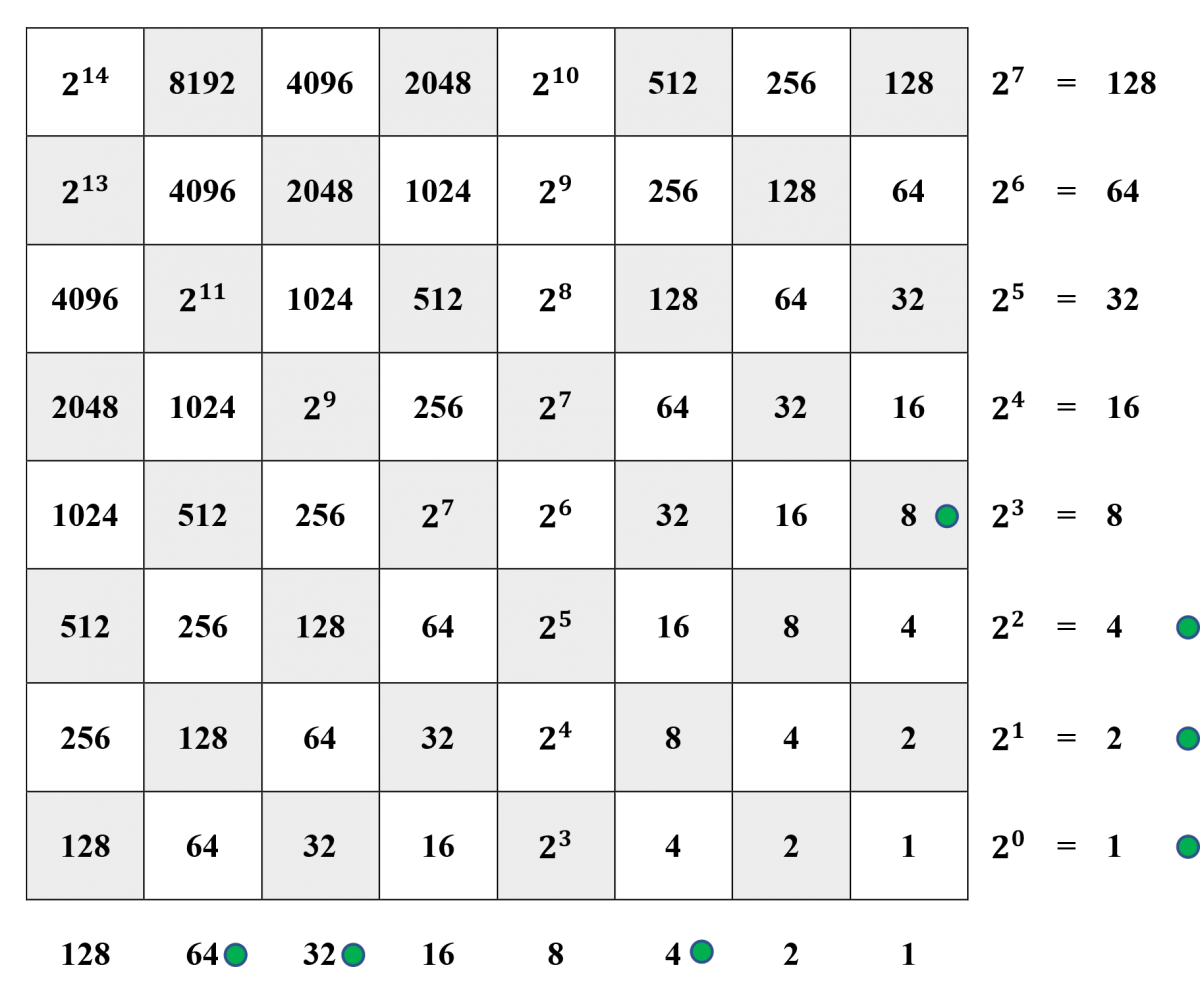
Steps 1 and 2. The dividend \(100\) is represented in the horizontal margin and the divisor \(7\) in the vertical margin. Since \(7\cdot 16 > 100,\) but \(7\cdot 8 \le 100,\) a counter has been placed on the 8-square in the right-hand column.
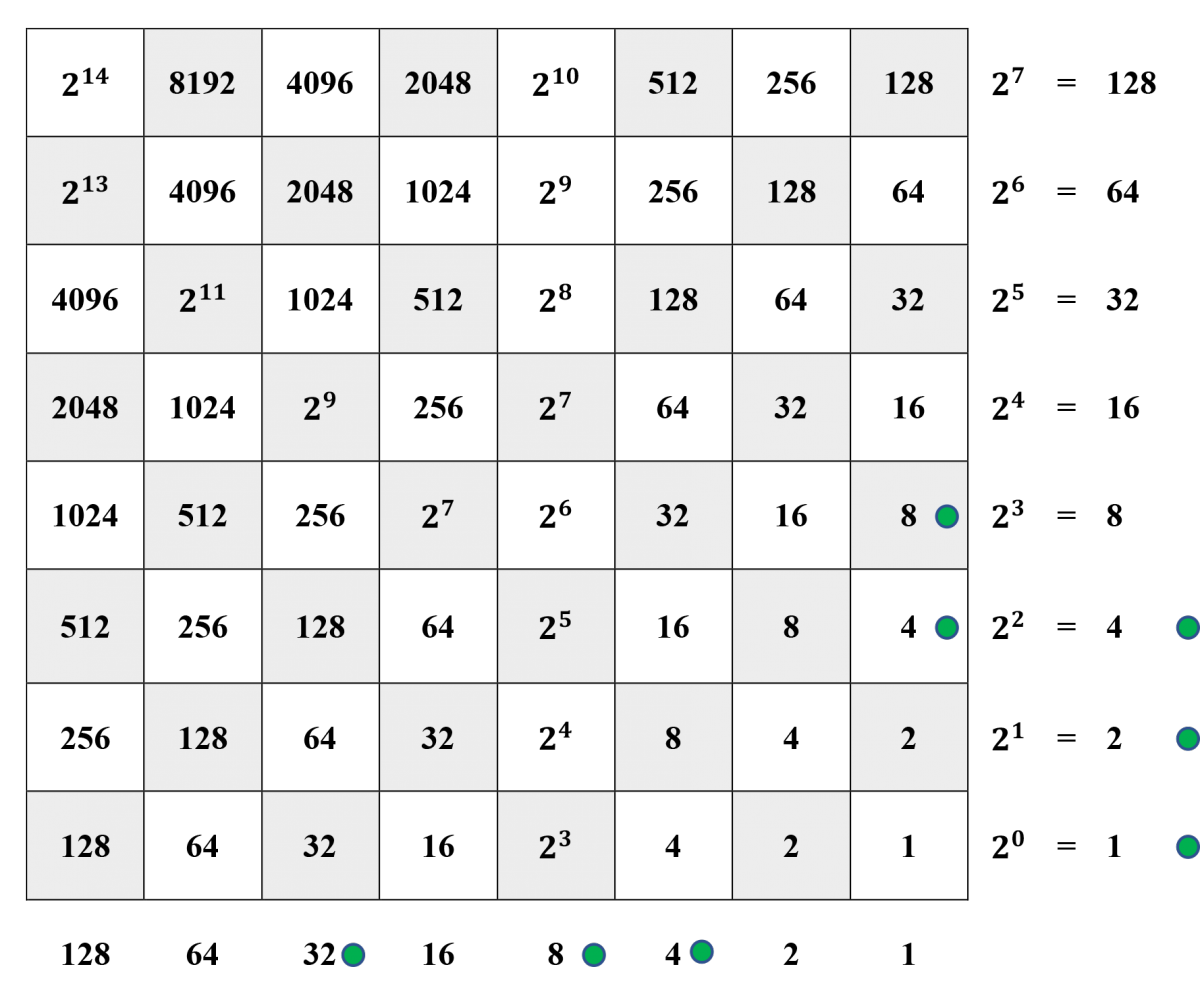
Steps 3 and 4. Since \(7\cdot 8 = 56,\) the current dividend is \(100-56 = 44,\) as represented in the horizontal margin. Furthermore, since \(7\cdot 8 > 44,\) but \(7\cdot 4 \le 44,\) a counter has been placed on the 4-square in the right-hand column.
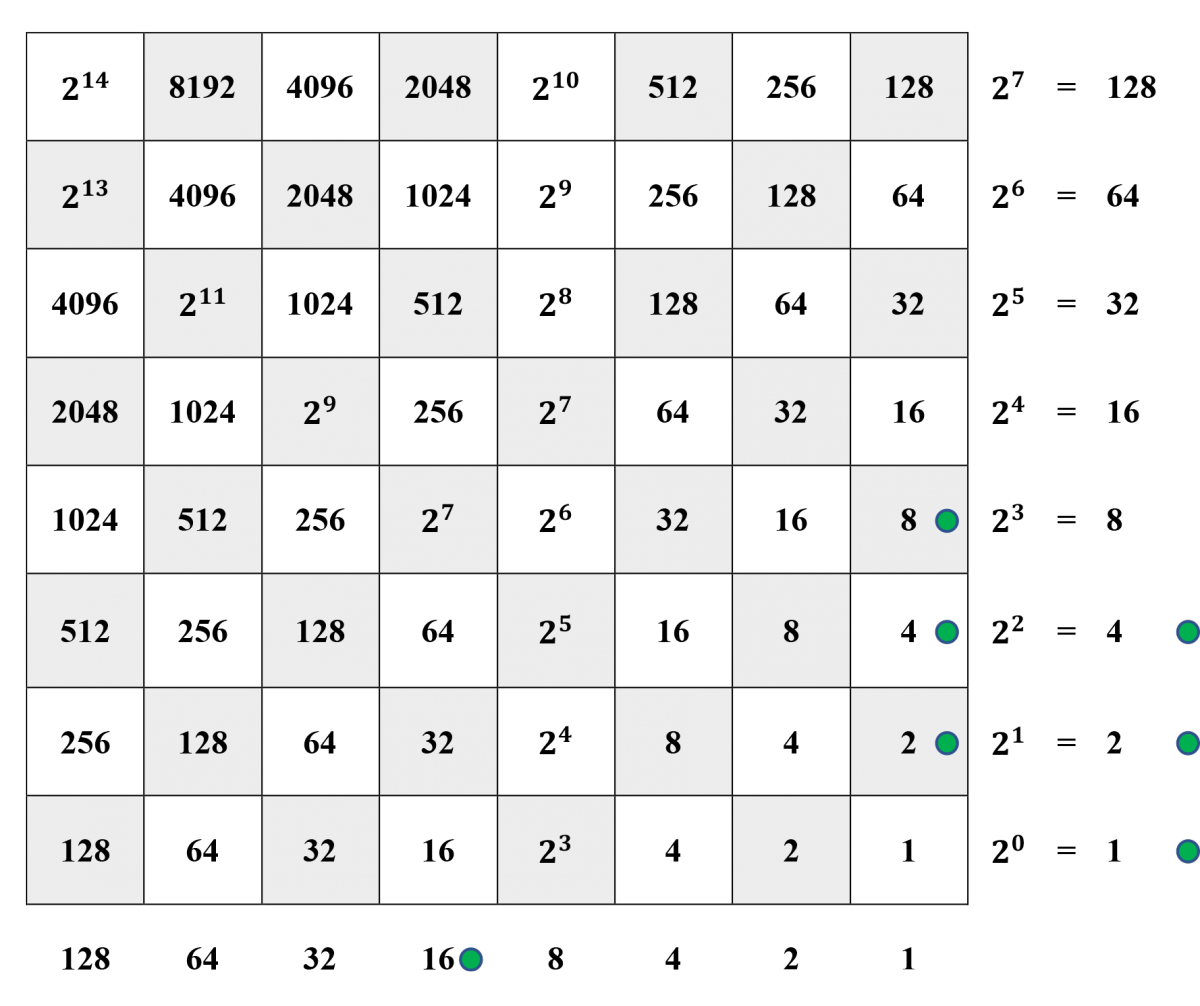
Step 4. Since \(7\cdot 4 = 28,\) the current dividend is \(44-28 = 16,\) as represented in the horizontal margin. Furthermore, since \(7\cdot 4 > 16,\) but \(7\cdot 2 \le 16,\) a counter has been placed on the 2-square in the right-hand column.
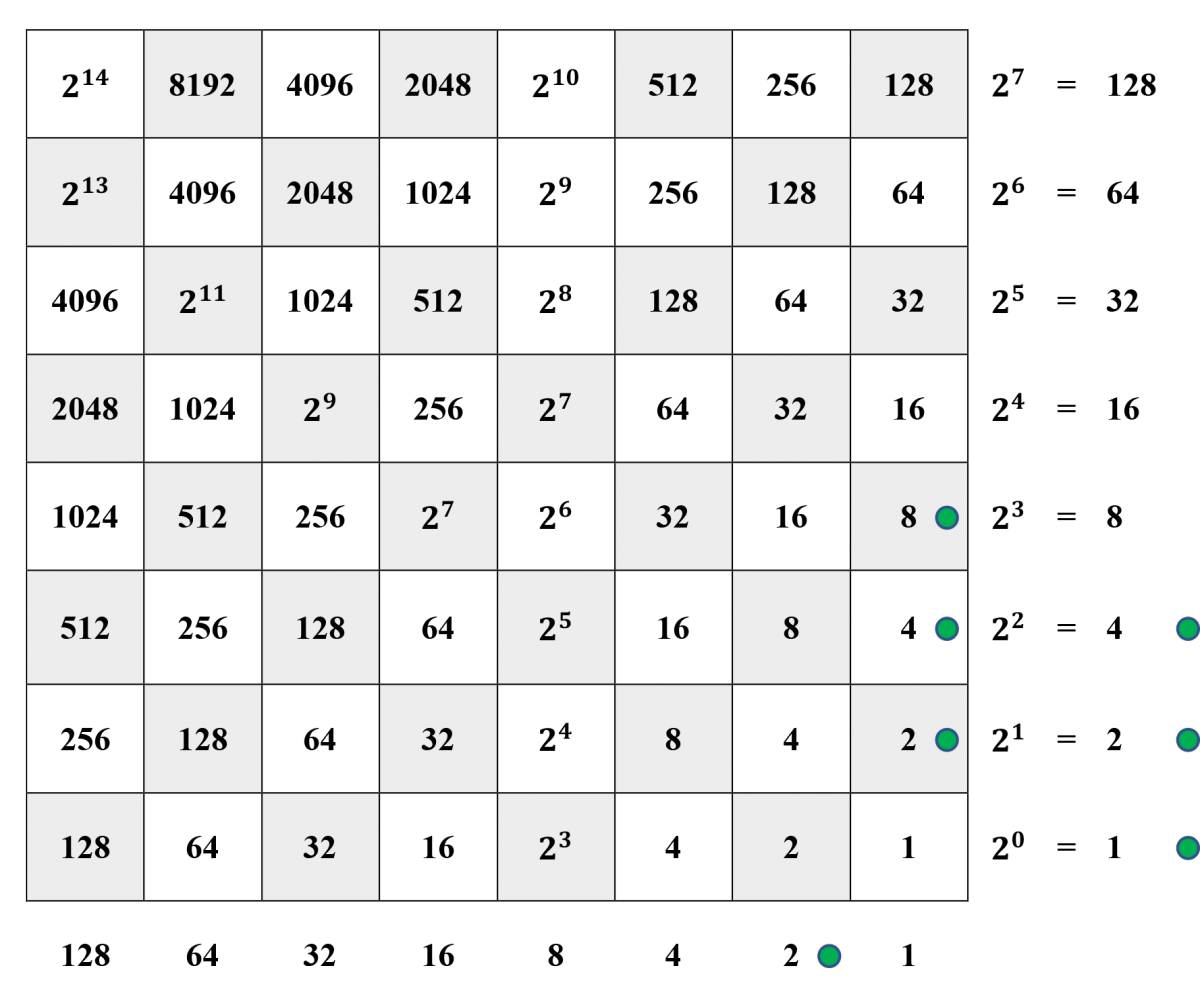
Step 4, continued. Since \(7\cdot 2 = 14,\) the current dividend is \(16-14 = 2,\) as represented in the horizontal margin. Since \(7\cdot 1 > 2,\) we cannot continue.
Step 5. We conclude that dividing \(100\) by \(7\) results in a quotient of \(8 + 4 + 2 = 14\) and a remainder of \(2.\)
Next: Extracting square roots on the chessboard calculator