A Classic from China: The Nine Chapters - Matrices
The Chinese counting board, with its grid of square cells, was also useful for storing and manipulating rows and columns of numbers, rather than rows and columns of single digits. Such a numerical grid was called a fangcheng, literally “divided rectangle”. Much later in the West, this would be called a matrix.
The Chinese were many centuries in advance of the rest of the world in using matrices to solve systems of linear equations. The coefficients of each equation were stored in one column, and the columns were filled from right to left. The numbers were then manipulated using the same types of operations described above for problems of excess and deficit: multiplying or dividing a column by a given number, adding or subtracting two columns, etc. To solve a system of linear equations, the rectangle of coefficients was reduced to triangular and then diagonal form, in a process identical to what Europeans would later call Gaussian Elimination.
The first problem in Chapter 8 involves the harvest of three different grades of rice:
Problem 7. Now given 3 bundles of top grade paddy, 2 bundles of medium grade paddy, [and] 1 bundle of low grade paddy. Yield: 39 dou of grain. 2 bundles of top grade paddy, 3 bundles of medium grade paddy, [and] 1 bundle of low grade paddy, yield 34 dou. 1 bundle of top grade paddy, 2 bundles of medium grade paddy, [and] 3 bundles of low grade paddy, yield 26 dou. Tell: how much [dou] does one bundle of each grade yield? (Shen et al., p. 399)
The following illustration shows how the above problem would be solved on a traditional Chinese counting board. Chapter 8 includes other problems with as many as six equations and six unknowns.
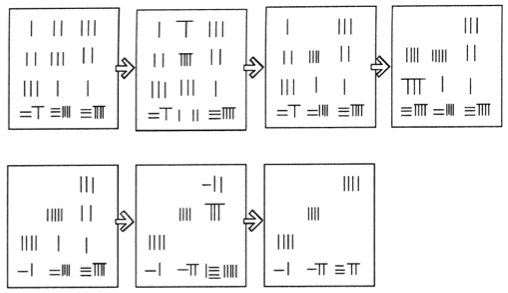
Illustration adapted from an article by Horng Wann-Sheng in HPM Newsletter 4:2b (Taiwan edition of the newsletter of the International Study Group on the History and Pedagogy of Mathematics)
Download solutions to Problems here: Students Explore the Nine Chapters from China.