In the spring of 1998, I volunteered to teach our History of Mathematics course, which, although it had a senior level number, had no prerequisite, and had only been taught on and off over the years whenever a faculty member showed interest at that moment. Often students with little or no background in mathematics enrolled. So, I decided immediately that a mathematics prerequisite was needed, that it should be taught as what our campus called a “writing intensive” course, and that it should be offered once a year, every year.

Writing intensive (WI) courses at UMKC now include the following relevant goals, which I helped compose. At the end of the course students should be able to:

• Demonstrate their ability through writing to read closely and analyze critically the texts of their disciplines.

• Produce writing through the recursive process of brainstorming, research, drafting, peer review, and revising.

• Use research methods and documentation that meet the standards of the discipline.

• Articulate and discuss their work with peers or the instructor.

WI course construction requirements include:

• The course design emphasizes and teaches writing as a recursive process.
  (The recursive process is defined as submission of one or more preliminary drafts for instructor response; peer review; revision of content, form, mechanics, and style, leading to a final draft.)

• Writing assignments are distributed throughout the semester and differ in length and purpose.

• The course requires a total of 5,000–10,000 words of revised, final-draft quality writing.

• Writing assignments account for at least 40 percent of the course grade.

In spring 2000, the course became designated Math 464 WI, History of Mathematics, writing intensive. [For more details see the Math 464 WI - Writing Intensive Chart (pdf)]. Since a writing intensive course is required for graduation at UMKC, all undergraduate students have completed a couple of basic writing courses by the time they are juniors to prepare them for such a course. So, I would not have to teach basic writing skills. Soon after Math 464 WI became writing intensive, I added the prerequisite of our On Solid Ground: Sets and Proof course, which itself has a prerequisite of Calculus II. Following these changes, I had classes of junior or senior mathematics majors or minors trained to write reasonably well, as well as read and understand proofs. The course quickly evolved into an introduction to the history of mathematics through the study of about forty proofs. The required texts have always included A History of Mathematics: An Introduction by Victor J. Katz, second or third edition; Journey Through Genius: The Great Theorems of Mathematics by William Dunham; and others as I found them useful. For example, I now also require How to Read Historical Mathematics by Benjamin Wardhaugh. Except for one year when it was cancelled, we have offered and I have taught Math 464 WI once a year each spring since 2000.

Students write two 4,000–5,000 word papers for my course, and the first and most time-intensive task for them is to choose a topic for each paper. This is never simple. Their incoming knowledge of the history of mathematics is shallow at best. So, to complement the resources within the Katz textbook (his References, Exercises, and Notes), I provide a list of print and internet sources for them to survey. (See Appendix 2.) I also bring in a subject expert librarian for one class who teaches them how to navigate library resources. In addition to our UMKC library, we are lucky to have located in the center of our campus the well-known private Linda Hall Library of Science, Engineering, and Technology, containing not only a huge collection of books in the history of mathematics, and subscriptions to journals like Historia Mathematica, but a well-stocked rare book room that houses dozens of historical mathematics books. (See the Convergence article: Mathematical Treasures at the Linda Hall Library, by Cynthia J. Huffman.)

For the first paper, I allow my students at least three to four weeks to trap a topic, with my help and their extensive searches. (Yes, it often seems like netting a darting butterfly.) I tell them a topic must have original documents (in translation) available, and those must include enough argumentation or proof for a healthy and required explication. (It is always dangerous to choose a mathematician who writes too well. In that case there may be little for a student to add. Example: Euler.) Below, I will only concentrate on the unique and most mathematical part of these papers.

At the beginning of the course, for practice students complete a couple of stand-alone explications of documents provided by me. Then, once they begin work on their papers, similar but different explicated documents that they discover become the core of those papers. In concentrating on explication, I am tapping into our mathematics students’ aptitude and interest in precise, technical work, the nuts-and-bolts of mathematical tasks. As well, I am tapping into their problem-solving inclinations and imagination in the form of detective work to discover what the author wrote. I tell them they have both the advantage and disadvantage of hundreds and in some cases thousands of years of mathematical progress and training in their background beyond that of the author they are reading. The advantage is that they can often “see through” what the arguments are leading to, as they jot notes in the margins using modern symbolism and graphs, and so on. The disadvantage is that by engaging that modern perspective they entirely miss the cultural context of the time, and in fact fail to “see” what the writer has written. Their modern understanding eclipses their attention to the details of what is on the page. We work on stripping back their “overview” to discern what is said and what is not said, what is assumed in that time period and what is anachronistic and ahistorical.

Explications must be “just in time.” It is annoying and loses the reader’s attention to read a long passage which makes little sense to them, only to be followed by a long explication. Such an explication is too late, and often hard to precisely align with the points in the passage where it is meant to apply. It also tempts the reader to ignore the original passage and just read the explication, which denies them the true understanding of the context as well as the substance of the arguments. I will tell students “The author is the focus, not you. With the assistance of your gentle guidance, your light touch, we want to be able to read the author’s work without pause.” I share with my students what the Oxford English Dictionary writes:

Explicate, verb:

1. a. To unfold, unroll; to smooth out (wrinkles); to open out (what is wrapped up): to expand ... 
   c. To spread out to view, display.
2. a. To disentangle, unravel.
3.     To develop, bring out what is implicitly contained in (a notion, principle, proposition).
4.     To unfold in words; to give a detailed account of … .
5.     To make clear the meaning of (anything); to remove difficulties or obscurities from; to clear up, explain.

To explicate is to cleverly, subtly answer questions before they are asked, so the reader, when he or she raises these questions, realizes the answer has already been handily provided. Thus, apprehension of the material and moments of clarity arrive more quickly because the reader’s intellectual struggle has been diminished by the explicator's apt remarks. An explication is not provided in order to train readers; it is instead to ease their path to understanding what the author wrote. Examples of helpful insertions include:

• A single word, or short phrase.
• An intermediary calculation.
• A contextual remark.
• A longer, separated discourse on its own line, where needed.
• Added diagrams or pictures, often in the form of a film strip of images leading to the desired configuration. This is helpful in geometry papers where only a single picture might be included in the original document that is better understood in fact as a sequence of pictures.
• Domains of variables.
• How extreme cases are handled, omitted, or overlooked.
• Adding enough links in the chain of reasoning that the mathematically knowledgeable reader is willing to trust any few pedestrian operations omitted.

            In the beginning, students are not sensitive to where these additions may be needed. For instance, they often include long explanations of parts well-written by the author (as an unconscious act, I think, to prove to themselves that they understand), and neglect spots of confusion that they “saw through” but which desperately require explanation. My job is to generously red ink their early attempts and point out where there is real need for explanatory assistance. I remind them, “It is harder to be clear than you think!”

            Here’s the sheet of advice I give my students for those short practice explications in advance of and separate from writing their papers, although of course the advice is universally useful. As I mentioned above, papers will then center on similar explications, but not consist solely of them. Note that their first task is to accurately type up the original source document, which seems easy, but often reveals a novice inattention to details like unusual or archaic spelling and capitalizations, grammatical oddities, and so on. This too turns out to be good practice for them.

Historical “Proof” Explication

• Read the given argument, proof, or theorem and proof combination. I have photocopied them from an original historical document, or faithful English translation. The assignment is designed to be more-or-less self-contained.
• Explicate this result, that is, write an expository version. Your version will usually therefore be longer than the original. Remember that a “proof” is a narrative, telling the story of (proving) why the theorem is true. Your job is to make that story transparent.
• Stay as close as possible to the style and form of the argument, preserving the historical flavor and ideas of the author. Do not substitute a faster, modern statement and proof.
• You will be graded on the clarity of your exposition.
• You will also be graded on how critically you have read the result, whether you found all the confusions, omitted or overlooked arguments, and so on, even if you were not able to settle all puzzles to your satisfaction.
• Your work may require any or all of the following:
  • Clarify words, definitions, and statements. For instance, "line" may be used where "line segment" is meant, "equation" confused with "expression", or "equal" with "congruent" or "equivalent"; the same letters or words may be used for several different objects; out-of-date terminology and phrasing may need to be updated, or just made more precise.
  • Is the result properly stated as a Theorem, Proposition, Lemma, Corollary, etc.? Is the Proof so named, and clearly delineated?
  • Add as many pictures as you like to clarify the argument. These include "idea" pictures, as well as the usual graphs, diagrams, constructions, etc. A detailed “movie” or “film strip” of images is often needed.
  • Include omitted arguments, or other details. Some arguments may be long enough to be stated (by you) separately as a Lemma. Do so, if you like. Other arguments may be knowledge assumed common by the author, but not clear to you or your modern readers. Tell us. This is vital to good exposition.
  • Correct any mathematical errors or omissions you may find. For example, if a variable suddenly appears in a denominator, did the author consider the case when that variable might be zero? Are there other omissions of cases we would today include? Are there typographic errors? Are the calculations really correct? Take nothing for granted.
  • Modernize the mathematical notation in your notes if needed, but again, stay close to the history.

When you read my Explications (and when you review your own)

• What changes did I make? Mark or circle them.
• Why do you think I made them?
• Was I reasonably faithful to the author's ideas?
• Are the pictures sufficient?
• Is the explication clearer than the original?
• Would you do anything differently or better? What exactly would you do?
• What did you learn about the author's strategy, ideas, methods, understanding?

I think it wise to provide examples to my students of what sort of explication product I expect. As I explain, I don’t require them to produce as complete a document as mine, but in reading my sample they should see what is possible with a little care and enough time on task. Every document requires multiple passes and close reading at both the level of fine detail and the level of structure and argumentation to reveal what explication is needed. A cursory glance (meaning just one quick draft) will inevitably miss important features, as I have found to my chagrin often enough in my own work. Here’s one of my samples. The original author’s document can be found here: Fibonacci On Two Birds Source (pdf). A second example document and my corresponding explication can be found in the following two documents: Alkhwarizmi Quadratic Equation Source (pdf) and Alkhwarizmi Quadratic Equation Explication (pdf).

 

One Explication SAMPLE provided to students

Math 464 WI                          History of Mathematics                                  R. Delaware

A Transcription and Explication using Modern English and Notation

From: Leonardo Pisano (Fibonacci), c.1170–c.1240, born in Pisa, in (what is now) Italy, from Liber Abaci (Book of Calculation), 1202, Chapter 13, Part One, as translated by L. E. Sigler in Fibonacci's Liber Abaci: A Translation into Modern English of Leonardo Pisano’s Book of Calculation, Sources and Studies in the History of Mathematics and Physical Sciences, New York: Springer, 2002, pp. 462–463.

Notes: All comments in [square brackets] and illustrations are mine.

 

On Two Birds

Two birds were above the height of two towers; one tower was 40 paces in height and the other 30, and they [the towers] were 50 paces apart; at an instant the pair of birds descended [from the tops of the towers] flying to the center [some point between the towers, not necessarily the exact center] where there was a fountain, and they arrived at the same moment at the fountain which was between both towers. From the moment they left until the moment they arrived they flew in straight lines from the tops of the towers to the center of the fountain; the flights were of equal lengths [distances];

[The unstated question is: Where is the center of the fountain located? Now, we start on a solution.]

in geometry it is clearly demonstrated that the height of either tower multiplied by itself added to the distance from the tower to the center of the fountain multiplied by itself is the same as the straight line from the center of the fountain to the top of the tower multiplied by itself [This is a statement of the Pythagorean Theorem, Euclid I.47.];

this therefore known, you put it that the distance from the center of the fountain to the higher tower is any number of paces, we say 10,

[a first “false position” guess. Here he begins an application of the so-called “Method of Double False Position” (which my students have already studied; see the Note following this explication). We’ll discuss below whether this is appropriate.]

and you multiply the 10 by itself; there will be 100 that you add to the height of the higher tower multiplied by itself, namely to 1600; there will be 1700 that you keep [the result of his first application of the Pythagorean Theorem to the “higher tower” right triangle], and you multiply by itself the remaining distance, namely the 40 which is the distance from the center [of the fountain] to the lower tower; there will be 1600 which you add to the height of the lower tower multiplied by itself, namely 900; this makes 2500 [the result of his second application of the Pythagorean Theorem to the “lower tower” right triangle] that should be 1700 [because the bird flights (hypotenuses) were of “equal lengths”] as was the sum of the other two products; therefore [the value of] this position is long of the true value by 800, namely the difference between 1700 and 2500

[The value of “this position” is really the difference “lower tower sum of squares – higher tower sum of squares”, a function of the “position”, which here is 10 paces. But, since the bird flights (each a hypotenuse) were of “equal lengths”, the squares of those lengths are then also equal, so by the Pythagorean Theorem the “true value” of “lower tower sum of squares – higher tower sum of squares” must therefore be zero!];

therefore you lengthen the distance from the center of the fountain to the higher tower; indeed it is lengthened 5 paces from the first position, namely 15 paces [the second “false position” guess] from the center [of the fountain] to the higher tower, and you multiply the 15 by itself; there will be 225 which you add to height of the higher tower multiplied by itself, namely 1600; there will be 1825. Similarly you multiply by itself the 35 which is the distance from the center of the fountain to the lower tower making 1225 [corrected from typographic error “12225”]; this added to the 900, namely the height of the higher [should be “lower”] tower multiplied by itself, makes 2125 that should be 1825 by the abovewritten [sic] rule [again, because the bird flights (hypotenuses) were of “equal lengths”]. Therefore the value of the second position is an amount long of the true value by 300

[Once again, the “value of the second position” is really “lower tower sum of squares – higher tower sum of squares”, a function of the “second position”, here 15 paces. So, the “true value” is again zero.];

the first value was long indeed by 800; therefore you say:

for the five paces which we lengthened the distance from the center of the fountain to the higher tower we approximated more closely to the true value by 500 [800 – 300 = 500]; how much indeed shall we lengthen the distance from the center of the fountain to the same higher tower in order to improve the approximation by [an additional] 300?

You multiply the 5 by the 300, and you divide by 500; the quotient will be 3 paces [written within a small “answer” box below]

[The idea is that when \(\frac{5}{500}=\frac{\Delta}{300}\), it follows that \(\frac{5\cdot300}{500}= \Delta=3\). The large box above is meant to suggest, reading horizontally, that since a change of 500 was caused by an increase of 5 paces, then a change of 300 will be caused by an increase of 3 paces. The two *s on the main diagonal indicate the multiplication of “5 by the 300”.]

which added to the 15 paces yields 18 paces, and this will be the distance from the [center of the] fountain to the higher tower. Truly the remaining distance, namely the 32 [which is 50 – 18], is the distance to the lower tower.

[Finally, he checks the solution.]

For example, the product of the 18 by itself added to the product of the 40 by itself makes as much as the product of the 32 by itself added to the product of the 30 by itself, as had to be. [18² + 40² = 32² + 30² (= 1924).]

 

A Modern Direct Solution

Let                \(x\)    =    the distance from the higher tower to the center of the fountain, so that

            \(50 - x\)   =    the distance from the lower tower to the center of the fountain.

By the Pythagorean Theorem, since the bird flight lengths (each a hypotenuse) are equal, and hence the squares of those lengths are equal, the problem requires that

                                    [Higher tower sum of squares] = [Lower tower sum of squares]:

\[\begin{array}{ccc} x^2 + 40^2 &=& (50-x)^2+30^2\\x^2 + 40^2 &=& 50^2 - 100x +x^2+30^2 \\ 100x + 40^2 -50^2 -30^2 &=&0 \\100x - 2\cdot 30^2 &=&0\\100(x-18)&=&0\\x&=&18\end{array} \]

 

So \(x= 18\) paces is the solution. Notice that it becomes clear at the third equation that in fact this is a linear equation (the “squared” powers add to zero) of the form \(ax = b\), justifying the use of the Method of Double False Position, which only applies to such linear relationships (functions).

 

Note: The Method of Double False Position

(called by Leonardo Pisano “elchataym”, an Arabic word)

[Based on comments by the translator L. E. Sigler of Leonardo Pisano’s Liber Abaci (Book of Calculation), 1202, translation published 2002, p. 628.]

Using modern notation, the idea is that to solve a linear equation \(ax+b=c\) for \(x\), pick two arbitrary values for \(x\), say \(x_1\) and \(x_2\) each of which is unlikely to be the correct value for \(x\), hence are in general called “false position” values. Substitute them into \(ax+b=c\)  to obtain \(ax_1+b=c_1\)  and \(ax_2+b=c_2\). From these two equations solve for both \(a\) and \(b\), then substitute those results back into \(ax+b=c\) , and finally solve for  \(x\) to get:

\[ x=x_2+\frac{(c_1-c_2)(x_2-x_1)}{c_2-c_1}.\]

In “On Two Birds,” \(x_1 = 10\), \(x_2=15\), \(c_1=800\), \(c_2=300\), and \(c=0\), the “true value,” yielding the quotient

\[\Delta =  \frac{(c_1-c_2)(x_2-x_1)}{c_2-c_1} = \frac{(0-300)(15-10)}{300-800}=\frac{-300(5)}{-500} = 3 ,\]

so that \(x = 15+3 = 18\), as desired. Also, in this modern notation, the proportion visualized in the “On Two Birds” box

\( \displaystyle{\frac{5}{300} = \frac{\Delta}{300}} \)    is     \( \displaystyle{\frac{x_2-x_1}{c_1-c_2} = \frac{\Delta}{c_2-c_1}} \)     

matching exactly the calculation of \(\Delta\) above (and avoiding the appearance of any negative numbers, which Leonardo would not have used).

 

A Modern Interpretation of the Leonardo Pisano Solution

Using \(x\) and \( 50 – x\) as above, he examines the function of  \(x\) (“the value of the position”) given by

                                   \[  f(x) = \mbox{ [Lower tower sum of squares] -[Higher tower sum of squares]} \] meaning    \[ f(x) = \left [ (50-x)^2 + 30^2 \right ] - \left [ x^2 + 40^2\right ] \]

which he desires to equal zero (the “true value”), that is, \(f(x) = 0\).

Using the Method of Double False Position (which does apply here since the function is actually linear), he first calculates

\( f(10) = 800      \)            then            \(      f(10 + 5) = 300 = 800 – 500  \) ,

determining the points (10, 800) and (15, 300) lying on the desired line, and he finds the solution by extending that line until it meets the horizontal axis. That is, he concludes that if an increase (from 10 paces) of  \(x\) by 5 paces yields a decrease of \( f(x) \)  by 500, then a further increase of  \(x\) by 3 paces will yield an additional decrease of \( f(x) \)  by 300, meaning a decrease to zero. Thus \( x = 15 + 3 = 18\)  paces is the solution.

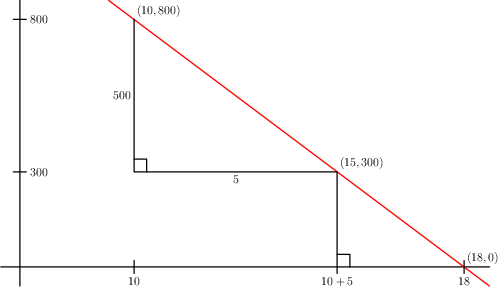
By the way, the equation of that line is \( y = 1800 - 100 x = 100 (18-x) \).

Here’s the handout I provide students about paper construction. (Additional technical details are in Appendix 1.) Of course, it is in the many conversations we have throughout the semester and multiple revisions that all these points begin to make sense to them.

Notes on the Writing of Expository Mathematics Papers

• Your paper is a narrative. It should tell a story, whether of a particular problem, result, or theory. So, include some history, tell us who did what when, share why your topic is important or interesting, and give us a beginning, a middle [where the proof(s) go], and an end!
• The proofs you will find in your research will be correct (usually!) but not necessarily as clearly explicated as an expository paper for your peer group (or me) requires. It is your job to provide written or mathematical clarifications, simplifications, added pictures, and other commentary to make the argument as clear as possible. One goal should not be the short, elegant, yet unenlightening proof, but rather a (possibly) longer, lucid, and revealing proof.
• You may likely find that figures, diagrams, graphs, and visual explanations of most kinds are sorely lacking in your sources. Or worse, in geometry sources you will often find a single massive detailed and frankly almost unreadable picture associated with a theorem or proof. In your explication of the proof expand the number of such figures, letting them evolve from the simple to the complex. As the proof proceeds, delete auxiliary aspects of figures once they have served their purpose, repeat pictures as needed so that your reader does not have to turn back several pages to follow your visual argument, and end with the completed result as your dramatic finish.
• Pictures should be near what they illustrate and should only be numbered if you plan to refer to them from some other page. If not, phrases like “see above” or “see below” suffice. Keep it simple.
• Use the terminology and conventions of modern mathematics (in English) correctly. For instance, the words “expression” and “equation” are not equivalent, “definitions” are not “assumptions”, “equal” is not “congruent”, and so on. Also, explain terms or abbreviations new to the reader, who, remember, has only been with you since your first page.
• Your paper should be as self-contained as possible. If you omit arguments and linkages, or “wave your hands” too much, your reader will justifiably abandon any attempt to follow your argument.
• Use standard conclusory terms with variety. For instance, choose from words or phrases such as thus, so, therefore, hence, whence, then, it follows that, we see that, we have, etc., when stating the many conclusions that appear in a mathematical argument. Otherwise, you risk putting your reader to sleep with repetition.
• If you draw from different sources, as you probably will, you often must unify the notation, sketches, and even the style. The reader should not have to switch for no reason from one set of variables or expressions to another set which symbolize the same ideas. This is sloppy writing, and only obscures your mathematical argument. Translate sources into a single language, unless of course it is those very differences that are the subject of your paper.
• Theorems, Definitions, Lemmas, Proofs, Constructions, Claims, Proofs of Claims, etc. should be indented and set off from the rest of your writing.
• I know that mathematical typography can be tedious on standard word processors, so do the best you can. Microsoft Equation Editor is often enough, but if you know other software feel free to use it. Just let me know. End your proofs with some sort of symbol, such as the black box █.
• Work with original sources (in translation) as much as possible. You’ll find original mathematical authors and other scholars are often not difficult to read, and even when challenging, well worth the effort.
• Consider written Internet sources suspect. Such work has usually not passed through the referee, review, and editorial scrutiny that all scholarly articles and books must. However, Internet sources can provide useful lists of references, and often enlightening illustrations or visualizations. I will be happy to look over anything you find on such sites.
• A paper should usually have at least three references, among them original sources in some form. Quoting actual documents for illustration or flavor is a good idea.
• Do not be too broad. For example, you might restrict to a few well-chosen and thoroughly explicated theorems as the core of your paper. The analysis of mathematics should be the core of your paper. A biographical, historical lead-in and a conclusion are just the frame.
• The level of discourse in your paper should be at least that of a student at this senior undergraduate level of mathematics.
•  A few ideas (not complete!) for types of papers:
  • Start with a modern statement of a theorem or problem and its proof. Research its history: various early proofs, counterexamples, errors, people and dates, variations, context … .
  • Start with a theory, or collection of ideas, and choose representative historical theorems to explicate.
  • Start with a person and choose his or her specific important theorems to explicate.

I also include “Advice from Writing Experts” (see Appendix 1).

Because the contest spring submission deadline is mid-semester, of the two papers written for my course only students’ first papers are ready on that date. However, as the rules allow, occasionally we have submitted second papers from the previous spring class. In all fourteen wins, eight were first papers, and six were second papers; eight authors were male, six female. Six of the topics were chosen by students, each a welcome surprise for me, and eight were topics resulting from my guidance. The papers we submit to the contest are a subset of those submitted for the course assignment that earn positive reviews from me. Nevertheless, my personal contest win prediction record is poor! I’m never certain that my evaluation criteria for the course will produce a win—another healthy way the contest encourages better writing, as I learn from which papers win how to (perhaps) improve my teaching next time. We just submit three to six such papers each year and trust to the judges.

Finally, I always look for other outlets for well-written undergraduate expository papers. Thankfully, some of the submitted  HOM SIGMAA contest papers and others written for the course have found print publication. [For a summary of my students' successes to date, see the table in UMKC-OtherPublications (pdf).]

At UMKC our English Department publishes annually The Sosland Journal, edited by English graduate students, that features essays by student winners of the Ilus W. Davis Writing Competition and other high quality papers: “The journal exhibits exemplary writing from both composition courses and university-wide writing intensive courses to be published and distributed to a larger audience, including UMKC students who use the journal as a textbook in select writing courses and the Kansas City community at large.” Since 2002, my students have been published there thirteen times and won eight awards.

In 2005, our UMKC Honors Program, now the Honors College, launched a journal called Lucerna, which is “interdisciplinary … and UMKC’s only journal … to cultivate and showcase original research and scholarship from the entire UMKC undergraduate community… peer-reviewed by a volunteer staff of student readers from the Honors College as well as faculty and staff from the Honors College.” My students have been published there eleven times since 2007.

In 2015, as I was looking for another publication opportunity for a couple of second student papers on more advanced topics, I discovered the Rose-Hulman Institute of Technology Undergraduate Mathematics Journal. Its description seemed promising, including (italics mine!): “devoted entirely to papers written by undergraduates on topics related to the mathematical sciences … each paper must be sponsored by a mathematician familiar with the student's work and … will be refereed. … Although the paper need not contain original research in mathematics, it must be interesting, well written, and at a level that is clearly beyond a typical homework assignment. Readers of the journal should expect to see new results, new and interesting proofs of old results, historical developments of a theorem or area of mathematics, or interesting applications of mathematics.” Two of my students’ papers survived the gauntlet of referees and were published there in 2016.

Finally now, the Honor Roll of UMKC  HOM SIGMAA winners is…

• 2004, Heath Yates, First Place co-winner: An Emanji Temple Geometry Tablet

• 2005, Newlyn Walkup, First Place winner: Eratosthenes and the Mystery of the Stades

• 2006, Samantha Reynolds, First Place co-winner: Maria Gaetana Agnesi: Female Mathematician and Brilliant Expositor of the 18^th Century

• 2010, Jennifer Nielsen, First Place co-winner: The Heart is a Dust Board: Abu’l Wafa Al-Buzjani, Dissection, Construction, and the Dialog Between Art and Mathematics in Medieval Islamic Culture

• 2011, Paul Stahl, Winner: Kepler’s Development of Mathematical Astronomy

• 2011, Rick Hill, Runner Up: Thomas Harriot’s Artis Analyticae Praxis and the Roots of Modern Algebra

• 2012, Jesse Hamer, Winner: Indivisibles and the Cycloid in the Early 17^th Century

• 2014, Anna Riffe, First Place co-winner: The Impossible Proof: An Analysis of Adrien-Marie Legendre’s Attempts to Prove Euclid’s Fifth Postulate

• 2014, Jenna Miller, First Place co-winner: Casting Light on the Statistical Life of Florence Nightingale

• 2014, Paul Ayers, Second Place co-winner: Gabriel Cramer: Over 260 Years of Crushing the Unknowns

• 2015, Samuel Patterson, First Place co-winner: Bernard Bolzano, a Genius Unnoticed in his Time

• 2017, Nathan Otten, First Place co-winner: Huygens and The Value of All Chances in Games of Fortune

• 2018, Callie Lane, First Place winner: Race to Refraction: The Repeated Discovery of Snell’s Law

• 2018, Rachel Talmadge, Second Place co-winner: François Viète Uses Geometry to Solve Three Problems
• 2019, Amanda Nethington, First Place winner: Omar Khayyam's Successful Replacement of Euclid's Parallel Postulate

 

[Editors' Note:  All winning papers in the HOM SIGMAA Student Contest are published in Convergence; most are also available through the HOM SIGMAA archives at http://historyofmathematics.org/archive/.]

About the Author

Richard Delaware has a Mathematics Ph.D. and is a Teaching Professor in the Department of Mathematics and Statistics at the University of Missouri – Kansas City (UMKC). In 2017, he won the UMKC Award for Excellence in Mentoring Undergraduate Researchers, Scholars, and Artists, in 2013 a small but meaningful Sosland Celebration Certificate of Achievement (for teaching writing) from the UMKC English Department, and in 2011 both the MAA Missouri Section Award for Distinguished College or University Teaching of Mathematics as well as the UMKC Provost’s Award for Excellence in Teaching. In 2018 he enjoyed the happy convergence of his background in theatre and his knowledge of the history of mathematics by creating copy for the mathematics posters used in the Kansas City Repertory Theatre’s production of “The Curious Incident of the Dog in the Night-time.”

Acknowledgements

The author thanks both editors and the three referees for sharp observations that substantially improved this article.

 

This appendix includes course requirements and advice on writing mathematics that I share with students in my course.

Basic Technical Paper Requirements in my Course

• Your paper must be typed.
• 12 point size font, Times New Roman preferred
• Double spaced for main text
• Single spaced for document or separate line quotations
• One inch margins
• Page numbers
• Word count at top right of first page
• 4,000–5,000 words usually, not including title page and works cited pages
• Later: A title page with working title, your name, the course, the date, draft number
• Later: Works cited page, numbered sequentially, listed alphabetically by first author, following MAA rules
• Your comments within a document text must be in [square brackets].
• Adding line breaks to the document text to break it into coherent parts is OK.
• Practice use of MS Equation editor, or other mathematical symbolic software
• Practice how to draw and include sketches or images; hand drawn figures are OK during draft stages

 

Advice from Writing Experts

From Strunk and White, The Elements of Style, 1972 edition:

• II-10:   Use the active voice.
• II-11:   Put statements in positive form.
• II-12:   Use definite, specific, concrete language: “deal in particulars and report the details that matter.”
• II-13:   Omit needless words.
• II-15:   Express co-ordinate ideas in similar form. [Extremely important in mathematics.]
• II-16:   Keep related words together. [Also, keep related pictures together with related words.]
• V-5:     Revise and rewrite.
• V-6:     Do not overwrite.
• V-7:     Do not overstate.
• V-16:   Be clear.

The references below, such as [6, p. 10], are to the list of publications about writing mathematics that follow these bullet points:

• From [6, p. 10]: “All the best writers whom I know read their work aloud to themselves. Reading your words aloud forces you to make sense of what you have written, and to deliver it as a coherent whole. If you have never tried this technique, then your first experience with it will be a revelation.”

• From [6, p. 92]: “Envision your reader sitting on a park bench reading your expository [paper], or putting his feet up and drinking a cup of coffee while reading. Do not imagine your reader with a pencil gripped in his fist, slaving away over each detail of your paper.”

• From [2, p. 8]: “Keep the reader informed of what you are doing and of how things stand. I have always enjoyed reading Sierpinski: first he tells you what he is going to do, then he does it, then he tells you he did it. … If you use a key term or symbol after a long spell without it, recall its definition or refer to where it was introduced. Your readers will be grateful.”

• From [2, p. 20]: “Write simple unaffected prose. Writing is harder than speaking because your tone of voice isn’t available to help make your point clear. Keep sentences crisp—think of what you want to say and say it. Mathematics is hard enough to read without convoluted writing that makes it harder.”

• From [5, p. 94]: “All writing benefits from revision. Your first attempt can always be made clearer, more concise, more forceful. Effective revision is a skill that is acquired through practice. … Put a draft aside for a few days, so that you can examine it with a fresh mind. Then analyze the draft in different ways. Read it aloud and listen to the rhythm. Read it at high speed. Does the text flow? Are the sentences of varying length? Read at the page level, focusing on the shape and the density of ink on the page. … Is there a good balance between equations and text? Does the paper look inviting? Do the key ideas stand out?”

• From [7, p. 90]: “There is a place for rigor in every kind of learning. All of us need to sharpen our thinking, and when we are challenged we should have to become more precise about what it is we are saying, how we are saying it, whether we are marshalling good arguments, and the like.”

• From [8, p. 11]: “Experienced writers know that they have to get something down on paper (or up on the screen) as fast as they can, just to have a draft that they can revise into a better one. … When you revise your early confusion into something clearer you better understand your own ideas. And when you understand your ideas better, you express them more clearly, and when you express them more clearly, you understand them even better … and so it goes.”

• From [9, p. 31]: “Care lavished on expression is not some optional embellishment bestowed upon your work; it is the means through which your work begins to exist. Your research turns up raw materials—very raw. Writing and rewriting make them into finished, usable products. Until brought out in full view by the best possible arrangement of words, your results remain incomplete, doubtful, hidden from every mind but your own. And your own, as your first draft shows, is none too clear.”

• From [9, p. 228]: “Rewriting is nothing but able tinkering. … Only an apprenticeship under a vigilant critic will gradually teach a would-be writer how to find and correct all the blunders and obscurities that bespangle every first draft.”

• From [9, p. 230]: “You discover what you really think by hacking away at your first spontaneous utterance.”

 

References on Writing Mathematics

1. How to Write Mathematics, Norman Steenrod, Paul Halmos, Menahem Schiffer, Jean Dieudonne, American Mathematical Society, 1973, 1981, 64 pages
2. Writing Mathematics Well: A Manual for Authors, Leonard Gillman, Mathematical Association of America, 1987, 49 pages
3. Mathematical Writing, Donald Knuth, Tracy Larrabee, Paul Roberts, MAA Notes, Number 14, Mathematical Association of America, 1989, 115 pages
4. Using Writing to Teach Mathematics, Edited by Andrew Sterrett, MAA Notes, Number 16, Mathematical Association of America, 1990, 139 pages
5. Handbook of Writing for the Mathematical Sciences, Nicholas Higham, Society for Industrial and Applied Mathematics, 1993, 241 pages
6. A Primer of Mathematical Writing, Steven Krantz, American Mathematical Society, 1997, 223 pages
7. Writing in the Teaching and Learning of Mathematics, John Meier, Thomas Rishel, MAA Notes, Number 48, Mathematical Association of America, 1998, 100 pages
8. Style: Ten Lessons in Clarity and Grace, 6^th Edition, Joseph M. Williams, Addison Wesley Longman, 2000, 309 pages
9. The Modern Researcher, 3^rd Edition, Jacques Barzun, Henry F. Graff, Harcourt Brace Jovanovich, 1977, 378 pages

This Appendix includes information on researching the History of Mathematics which I share with  students in my course.

Print Sources

Sources of Original Mathematical Documents in Translation

• A Source Book in Mathematics, David Eugene Smith, Dover, 1959.
• A Source Book in Mathematics, 1200-1800, ed. Dirk J. Struik, Harvard University Press, 1969.
• Classics of Mathematics, ed. Ronald Calinger, Prentice Hall, 1995.
• The History of Mathematics: A Reader, ed. John Fauvel & Jeremy Gray, Open University, MacMillan Press, 1987.
• Pi: A Source Book, J. L. Berggren, Jonathan Borwein, & Peter Borwein, Springer Verlag, 1997.
• A Source Book in Medieval Science, ed. Edward Grant, Harvard University Press, 1974.
• From Kant to Hilbert: A Source Book in the Foundations of Mathematics, Vols 1 & 2, William B. Ewald, Oxford University Press, 1996.
• A Source Book in Classical Analysis, Garrett Birkhoff, Harvard University Press, 1973.
• Euclid, the Thirteen Books of the Elements, vols 1,2,3, trans. by Thomas L. Heath, Dover, 1956.
• Contributions to the Founding of the Theory of Transfinite Numbers, Georg Cantor (1915), Dover, 1955.
• The Early Theory of Equations: On Their Nature and Constitution, Golden Hind Press, 1986, contains translations of (pp.1–104) On the Recognition of Equations, by François Viète, 1615; (pp. 105–148) A New Discovery in Algebra, by Albert Girard, 1629; (pp. 149–218) On the Nature and Constitution of Equations, by Florimond de Beaume, 1657.
• The Mathematics of Egypt, Mesopotamia, China, India, and Islam, A Sourcebook, ed. Victor J. Katz et al., Princeton University Press, 2007.
• Sources in the Development of Mathematics – Series and Products from the 15th to the 21st century, Ranjan Roy, Cambridge University Press, 2011.
• Mathematics Emerging: A Sourcebook 1540-1900, Jacqueline Stedall, Oxford, 2008.
• Sourcebook in the Mathematics of Medieval Europe and North Africa, ed. Victor J. Katz et al., Princeton, 2016.

General Histories of Mathematics and References

• A History of Greek Mathematics, vols 1,2, Thomas L. Heath, Dover, 1981 (1921).
• Mathematical Thought from Ancient to Modern Times, Morris Kline, vols 1,2,3, Oxford Univ. Press, 1972.
• Great Moments in Mathematics (Before 1650), Howard Eves, Dolciani Mathematical Expositions, Mathematical Association of America (MAA), 1983.
• Great Moments in Mathematics (After 1650), Howard Eves, Dolciani Mathematical Expositions, MAA, 1983.
• Math through the Ages: A Gentle History for Teachers and Others, William P. Berlinghoff and Fernando Q. Gouvêa, expanded second edition, MAA 2015.
• Non-Euclidean Geometry, Roberto Bonola, Dover, 1955. [Includes translations of Bolyai and Lobachevsky papers.]
• A History of Numerical Analysis from the 16th through the 19th Century, Herman H. Goldstine, Springer, 1977.
• The Mathematics of the Heavens and the Earth: The Early History of Trigonometry, Glen Van Brummelen, Princeton, 2009.
• A History of Algorithms, From the Pebble to the Microchip, Jean-Luc Chabert et al., Springer, 1999.

Specific Problems or Theorems

• The Trisection Problem, Robert C. Yates, National Council of Teachers of Mathematics (NCTM) Classics in Mathematics Education, 1971.
• The Pythagorean Proposition, Elisha Scott Loomis, NCTM Classics in Mathematics Education, 1972.
• 100 Great Problems of Elementary Mathematics, Their History and Solution, Heinrich Dorrie, trans. by David Antin, Dover, 1965.
• A Mathematical History of the Golden Number, Roger Herz-Fischler, Dover, 1987.

Individual Mathematicians

• Archimedes, E. J. Dijksterhuis, Princeton Univ. Press, 1987.
• Archimedes: What Did He Do Besides Cry Eureka?, Sherman Stein, Mathematical Association of America, 1999.
• The Works of Archimedes, with the Method … , Thomas L. Heath, Dover, 1897.
• Archimedes in the Middle Ages, 10 vol., Marshall Clagett, University of Wisconsin, 1964.
• Aristarchus of Samos, The Ancient Copernicus, Thomas L. Heath (1913), Dover, 1981.
• Diophantus of Alexandria, A Study in the History of Greek Algebra, Thomas L. Heath, Dover, 1885.
• Leonardo Pisano (Fibonacci): Liber Abaci (Book of Calculation, 1202), trans. L.E. Sigler, Springer Verlag, 2002.
• Leonardo Pisano (Fibonacci): Liber Quadratorum (Book of Squares, 1225), trans. L.E. Sigler, Springer Verlag, 1987.
• Nicolas Chuquet, Renaissance Mathematician, ed. Graham Flegg et al., Springer, 1985, translation of parts of Triparty, 1494.
• Cardano, the Gambling Scholar, Oystein Ore (1953), Dover, 1965.
• Galileo Galilei: Two New Sciences, etc., trans. Stillman Drake, Univ. of Wisconsin Press, 1974.
• The Analytic Art, Francois Viete, trans. by T. Richard Witmer, Kent State University Press, 1983.
• Nicole Oresme and the Medieval Geometry of Qualities, ed. Marshall Clagett, Wisconsin, 1968.
• John Wallis, The Arithmetic of Infinitesimals, 1656, trans. by Jacqueline Stedall, Springer, 2004.
• Euler, The Master of Us All, William Dunham, Dolciani Mathematical Expositions, MAA, 1999.
• The Mathematical Career of Pierre de Fermat 1601-1665, Michael Sean Mahoney, Princeton Univ. Press, 1973 (2nd Edition, 1994).
• Kepler's Physical Astronomy, Bruce Stephenson, Springer-Verlag, 1987.
• The Mathematical Works of Bernard Bolzano, Steve Russ, Oxford, 2005.
• Cauchy’s Cours D’Analyse, annotated translation by Rob Bradley and Ed Sandifer, Springer, 2009.
• Georg Cantor: His Mathematics and Philosophy of the Infinite, Joseph Dauben, Harvard University Press, 1990.

Chinese and Japanese Mathematics History

• Chinese Mathematics in the Thirteenth Century, Ulrich Libbrecht, Dover, 1973.
• Fleeting Footsteps: Tracing the Conception of Arithmetic and Algebra in Ancient China, Lam Lay Yong and Ang Tian Se, World Scientific, 1992.
• A History of Japanese Mathematics, David Eugene Smith and Yoshio Mikami, Dover, 1914.

Islamic Mathematics

• Episodes in the Mathematics of Medieval Islam, J. L. Berggren, Springer Verlag, 1986.

Probability, Statistics, Graph Theory, Number Theory

• Games, God, and Gambling: The Origins and History of Probability and Statistical Ideas from the Earliest Times to the Newtonian Era, F. N. David, Hafner Publishing,1962.
• A History of Probability and Statistics and Their Applications Before 1750, Anders Hald, Wiley, 1990.
• The Doctrine of Chances, 3rd edition, A. De Moivre, 1756. Available through the American Mathematical Society (AMS).
• The Logic of Chance, John Venn, 3rd edition, 1888, Dover, 2006.
• The History of Statistics, The Measurement of Uncertainty before 1900, Stephen M. Stigler, Belknap Press, 1986.
• Graph Theory 1736–1936, Norman L. Biggs, E. Keith Lloyd, and Robin J. Wilson, Oxford, 1976.
• History of the Theory of Numbers, vols. 1-3, L. E. Dickson, Chelsea, 1919, Dover, 2005.
• Number Theory and Its History, Orestein Ore, McGraw-Hill, 1948.
• Combinatorics, Ancient and Modern, eds. Robin Wilson and John Watkins, Oxford, 2015.

High Quality Internet Resources

Many of these resources have links to other sites of interest. Be critical of the information you find!

• MacTutor History of Mathematics Archive (Highly recommended!)
• The Math Forum @ Drexel: Math Topics: History/Biography
• History of Mathematics (University of Tennessee at Knoxville)
• The History of Mathematics (Trinity College, Dublin)
• Historia Mathematica (Journal of the History of Mathematics)
• The Visual Elements of Euclid (Books 1-6, each proposition broken down into a series of colored graphics)
• Archimedes Home Page
• The Euler Archive
• The Analyst of George Berkeley (Entire Text)
• History of Statistics
• Convergence
• Biographies of Women Mathematicians