What a strange question to ask, especially on an MAA website. I hope it has attracted the reader’s attention and curiosity. The words of the title, in themselves, pose an important and controversial question, but the statement is not complete. The whole question is: "Do we teach too much mathematics but not enough about it?" In my experience, I have taught mathematics for over fifty years, covering a broad spectrum of people and situations: from pre-school to graduate classes and from intercity America to the rural compounds of lesser-developed countries. Always, I have been plagued by the students’ recurring questions—“What is this stuff good for?” “When will I ever use this?”—and still further perplexed by an adult’s apologetic confession that he or she “never liked mathematics and was confused by it.” Elementary school teachers, if given a choice, will opt out of teaching mathematics in favor of other subjects. Mathematics has a bad reputation! This negative situation seems universal.

In attempts to isolate and remedy these situations of frustration, I have come to believe that the fault most often can be found in the ways we teach mathematics. Too often instruction consists mainly of sequences: concept, exercises, repeat; or definitions, algorithms, practice, test. Teach the mechanics—impart the skills. I know, I’ve been there, we must get through the syllabus! But mathematics has a story to tell; it has a structure, a history and a purpose. All these factors, if recognized and acted upon, do in fact lead to better appreciation and understanding of the subject and eventually to an improved student performance. However, most often, they are neglected or minimized. Better teaching would stress the affective aspects of mathematics teaching and learning—what we might call ‘humanizing mathematics’, that is, better exposing and building upon its historical, societal and cultural connections. We might also think of this as ‘doing a better job of selling the subject', thus responding to the complaint: "What is this stuff good for?”

One of the earliest extant mathematical texts on problem solving is prefaced with the inducement that accurate reckoning as explained in the book will provide the user with: “The entrance into the knowledge of all existing things and all obscure secrets.” The text is the Egyptian Rhind Mathematical Papyrus, composed about 1650 BCE (Chace 1979, p. 27). What reader could resist the power promised by learning numbers and how to compute with them? Over two thousand years later, we find the Chinese master scholar Sun Zi exhorting the readers of his arithmetic book, Sun Zi suanjing with similar claims:

Mathematics [governs] the length and breadth of the heavens; [it affects] the lives of all creatures. ... [Mathematics] has prevailed for thousands of years and has been used extensively without limitations. If one neglects its study, one will not be able to achieve excellence and thoroughness (Lam and Ang 1992, pp. 151–152).

The scope and comprehensiveness of Zi’s claim impacted the Mandarins or court officials on whose knowledge the existence and harmony of their Celestial Empire depended.

In 1543, Robert Recorde, an English physician, wrote one of the first English-language mathematics texts for the common folk of his country: The Ground of Artes, Teachyng the Worke and Practice of Arithmetk. As a motivation, he noted: “yf nombre be lackynge, it maketh men dumme, so that to most questions, they must answer mum” (Wilde 2014). The readable, nonacademic Ground of Artes became so popular that it went through 47 printings by 1699. Its text, written as a dialogue between a teacher and his pupil, devoted much of its effort to promoting the value and usefulness of mathematics.

In a somewhat similar manner, it was a common practice for 19th-century mathematics textbooks in the United States to carry an endorsement by some prominent citizens as to the value and worth of the material about to be studied. Additionally, many arithmetic texts of this period, both in Europe and North America, bore the word “commercial” in their titles. Even those not so named emphasized business applications in their word problems. There was little confusion about where and how the mathematics would be employed. (See Figure 1.) Thus, from ancient times up to the 20th century, the learning of mathematics was highly motivated and directed. Its contemporary relevance and usefulness was stressed. Mathematics was a powerful tool, whether in the pursuit of magical ponderings, bureaucratic administration, or the earning of a living. It had an important, recognizable, and appreciated human value.

Figure 1. Text written by Jonas Moore for his students at the Royal School of Mathematics, London, 1681. This was one of the first British institutions devoted to the teaching of mathematics to the common working-class man. The applications of mathematics are clearly stated on the title page and developed within.

In our modern period, education has been homogenized in the service of making it more accessible. It may be questionable whether a particular status can or should be ascribed to any particular subject in the common curriculum by authorities. However, at the discretion of the individual classroom teacher, and as needed by the students, a promotional effort could be applied to certain subjects. Due to its continuing stigma, I believe strongly that mathematics is one of these teaching areas that requires still better answers to the questions “What?” “How?” and “Why?”

Starting with the “What?” It's mathematics! "Well, then what is mathematics?" This is a question every teacher of mathematics should confront. In high school, we usually teach algebra before geometry. Both are mathematics; how are they the same? What is the common thread? The (hidden) connection perplexed me as a student. I’ll supply an answer but readers should also seek their own. Mathematics is a study of relationships and implications. It has a structure and is a deductive science. A learner identifies quantity by examining sets of different sizes and arriving at an ordering cognitively and then, perhaps, physically—thus symbols such as >, <, = and ≠. Differences are then distinguished by use of a measure and numbers. With the addition of operations, a working structure for arithmetic is established. Patterns appear. A process of repeated addition leads to the operation of multiplication and in a similar manner, the recognition of multiplication and division as inverse operations provides methods for computational checks involving these operations. In geometry, the perpendicularity of two lines implies the existence of right angles. In the study of calculus, a definite integral —> a derivative —> mathematical change. And so it goes on: one concept leading to another. A good textbook, or scope and sequence, would be mindful of such a progression of implications. It is an understanding of this network of connections that we want to impart to students. But in appreciating this “What?” the humanity of mathematics—the peoples, cultures, times and places—should also be mentioned.

Confronted with such an idea, often a teacher will respond; “I teach mathematics and have no time for history!” An understandable response, but I would counter that the teaching of a subject also involves the teaching about a subject. No extensive diatribe is required—just a word or comment, an analogy, or pointed reference to a visual illustration. [1] For example, in a lesson involving the operation of division, a teacher might interject “that during the Middle Ages, performing division was considered very hard, it was called the Iron Operation and there were several algorithms for attempting the task." (See Figure 2.) Noting that Italian merchants (such Marco Polo, Luca Pacioli, and Fibonacci) were the group of people who really developed our arithmetic relates people with mathematics. In a similar manner, algebra should be associated with the Arab word “al-jabr”; the name “Euclid of Alexandria” mentioned in geometry lessons; the Newton-Leibniz controversy cited to add intrigue and relevant questions to the understanding of calculus. Often the historical sequence in the development of a concept suggests the pedagogical approach used in the classroom.

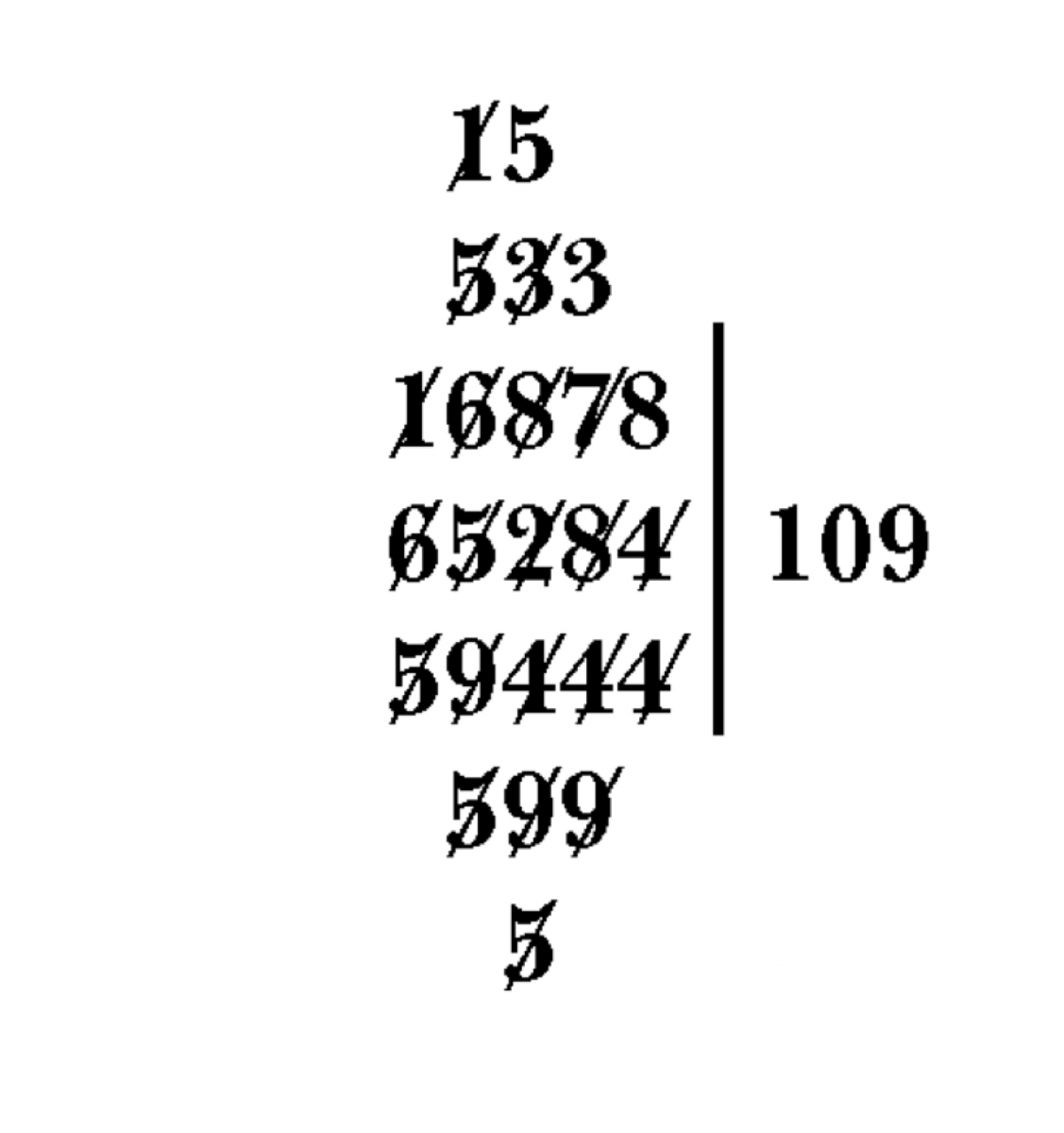
Figure 2. “Galley Division” was the most popular European form of division. Each algorithm bore a distinctive name to assist in its memorization. “Galley” refers to a ship’s sails. At left above, the quotient of 65284 divided by 594 is found to be 109 538/594. While this technique was considered fairly easy to use, printers did not like it and it fell out of fashion. The figure at right above, from Hodder's Arithmetic (9th ed., 1671, pp. 54–55), may help illustrate printers' objections.

For example, the trigonometric functions are first introduced as discrete ratios found from a right triangle, ratios that were first realized through the physical task of “shadow reckoning”; projected heavenly, they became continuous, circular functions, derived from sweeping arc lengths. (See Figure 3.) Ask open-ended questions—let pupils find out, for instance, “Why is the weight measure 'pound' abbreviated as 'lb.'?" “Did Pascal really discover Pascal’s Triangle?" “Why is division by zero undefined?” Little mysteries, inserted as an aside, arouse curiosity and often further enhance self-learning. So mathematics is revealed as a structured, deductive science; a game, with a long history and played by humans, where the number of rules and pieces constantly increase, a game in which our students are invited to participate. Pedagogical emphasis on the structure of mathematics, to be fully successful, should be a cooperative effort within a school system. From at least the middle-school level onwards, mathematics teachers ought to recognize and follow a similar deductive teaching strategy that constructs a chain of understanding for their students.

Figure 3. In 1532, the scholar and instrument maker Peter Apian published Quadrans Apiani astronomicus, an instructional manual on the use of the quadrant. In this illustration from Apian’s book, a quadrant, rather than the available shadow of a tower, is used to find the inclination of the sun’s rays. From the information provided, can you determine this angle?

Notes:

[1] The Mathematical Association of America maintains an archive of historical mathematical images, “Mathematical Treasures”, available free of charge for use by teachers: https://www.maa.org/press/periodicals/convergence/index-to-mathematical-treasures.

As for the “How?” of mathematics—its calculations and mechanics—this aspect of teaching is probably the strongest existing suite. Most teachers I know do a good job in this area. But, once again, try to humanize this effort. Calculation and problem solving have a long history containing many curiosity-arousing facts and episodes of experimentation. For example, the Chinese wrote their common fractions “upside down” with our denominator, called “the mother”, on top; below was our numerator, “the son”. In medieval Europe, at least five algorithms for the multiplication of two multi-digit numbers were employed. The Zuni people of America had seven directions for relating location (What were they?), and the mathematically admired “Golden Rule” was a technique involving a simple proportion (Smith 1958, II:484). Problems from other cultures and distant historical periods can be assigned, affirming that our ancestors did much of the same mathematics we do today. Worked calculations performed centuries ago can be resurrected and reexamined to affirm their correctness. (See Figure 4.) Even Pharaoh’s scribes in ancient Egypt made mistakes!

Figure 4. Synopsis Algebraica (1693) was written for the teaching of mathematics at Christ’s Hospital, London. The interesting feature of this book is that it is a mathematical workbook; opposite each page of text is a blank page allowing for annotations and computations. Little is known about the original Swiss author, Johann Alexander. Above, an 18^th-century student attempts to solve problem 35 by allowing EG=x, FG=y, EF=c, DE=b and DF=a; setting up an equation to represent the mathematical situation; and solving for the required unknown, “x”. By the customs of the period, a squared quantity is designated, in print, by repeating it twice. Is the computation shown correct? An English-language version of the book was published in 1709.

Now, for the “Why?” "Because it’s going to be on the test!" is the usual response. Prodding and threatening, yes, but not cognitively satisfying. Can we convey an appreciated value, from the past, present or future? Historically, every mathematical concept has had a motivation, a purpose. While the concept may be produced by the mathematics itself, sufficient real world examples are available for reference. The right triangle determines “vertical and horizontal.” Geometry and trigonometry gave rise to efficient surveying and navigation; instructors might ask, "What was the Great Trigonometric Survey?" [1] "How much was the prize for finding a method to determine longitude at sea?" Decimal fractions were needed to make precise measurements, so "why does a clock face mark only twelve hours?" In answering or referring to such questions, the query “Why?” often guides students to a deeper understanding than alternately-directed inquiries.

While historical relevance can motivate learning, allusions to contemporary relevance should have a teaching/learning rationale. In the 1950s, I had an algebra class where I was introduced to matrix computation. The teacher was a “name dropper”. In the process of instruction, he would casually include such names and terms as “IBM”, the “Rand Corporation”, “Think Tanks”, “Game Theory”, and “Markov Chains”. Some words we recognized with respect; others, for example ”Markov Chains”, were completely foreign but fascinating in their implications. I remember researching the concept of a Markov Chain, learning something about its development and, mathematically, playing with one. Of course, I also did my assigned work with matrices. Here the teacher was knowledgeable about the applications of mathematics, contemporary and potential, and shared his knowledge with the class, encouraging and motivating us as to the uses of mathematics.

More than an appeal to authority, I believe the best way to secure a student’s respect for problem solving is to give good, relevant problems. Observing an Algebra II class that just completed a problem in mathematically modeling an irrigation situation, I heard a young participant exclaim, “Now, that’s real mathematics.” I hope we teach “real” mathematics (Swetz and Hartzler 1991, p. 52). Interpreting data from the current news media on economic predictions or political polls is a fertile field for culling mathematical problems. Modeling problems involving contemporary environmental situations—global temperature rise, species extinction, ocean and air pollution, population growth, disease prevention—can assert the value of mathematics and, further, even promote meaningful discussion: "Is the ban on elephant poaching in Africa having an effect on ivory production?" "In which country is the human population increasing the fastest? Why?" Such questions focus both on contemporary issues and on issues our young people will continue to confront throughout their lives. This is the “New Math” of the millennium together with STEM priorities. [2] Our students must have the experience and knowledge to recognize the problems and the capability to resolve them.

Notes:

[1] Several questions have been left open for the reader to consider. Using information-supplying electronic devices, answers are easy to secure; however, I will assist with these immediate inquires. The Great Trigonometrical Survey was a project instituted by Great Britain intended to measure and map the entire Indian subcontinent with scientific precision. It was begun in 1802 by the infantry officer William Lambton under the auspices of the East India Company. His successor was George Everest, for whom the highest mountain in the world would be named. The project was completed in 1871. What mathematical techniques and concepts were employed?

For the seeking of a convenient and accurate method of determining a measure of longitude at sea, the British Navy established a Board of Longitude. This agency offered a prize/reward of £20,000 for the solution. What classroom exercises could be developed from this incident?

For the efficient operation of a clock face, a system of modulus 12 numeration and arithmetic is employed. What is modular arithmetic?

[2] STEM is a curriculum based on the idea of educating students in four specific disciplines: science, technology, engineering and mathematics, in an interdisciplinary and applied approach. See https://www.livescience.com/43296-what-is-stem-education.html.

Mathematics teachers, like most teachers, are bombarded with advice on how better to do their job. While well meaning, much of this is irrelevant or impractical. I offer a whispered suggestion, a humble opinion based on experience. Such a social-historical approach in teaching should have been evident in our training and mathematics education. Unfortunately, most often it was not. The task of change is up to us. It begins in pondering and personally resolving the question, “Do we teach too much mathematics . . . ?”

Alexander, Johann. 1693. Synopsis Algebraica. London: Benjamin Motte.

Apian, Peter. 1532. Quadrans Apiani astronomicus. Ingolstadt.

Chace, A. B. 1979. The Rhind Mathematical Papyrus. Reston, VA: The National Council of Teachers of Mathematics. Reprint.

Cocker, Edward. 1644. Arithmetick. London: John Hawkins.

Hodder, James. 1671. Arithmetick. 9th ed. London: Thomas Rooks.

Lam, Lay Yong, and Ang Tian Se. 1992. Fleeting Footsteps: Tracing the Concept of Arithmetic and Algebra in Ancient China. Singapore: World Scientific Press.

Moore, Jonas. 1681. A New System of Mathematicks. London: A. Godbid.

Recorde, Robert. 1543. The Ground of Artes. London: Reynold Wolff.

Smith. D. E. 1958. History of Mathematics. 2 vols. New York: Dover Publications. Reprint.

Swetz, Frank, and Jefferson Hartzler. 1991. Mathematical Modeling in the Secondary School Curriculum. Reston, VA: The National Council of Teachers of Mathematics.

Wilde, Lisa. 2014. ‘Whiche elles shuld farre excelle mans mynde’: Numerical Reason in Robert Recorde’s Ground of Artes (1543). Journal of the Northern Renaissance, http://www.northernrenaissance.org/whiche-elles-shuld-farre-excelle-mans-mynde-numerical-reason-in-robert-recordes-ground-of-artes-1543/.