Introduction

I will present Cardano's solution to the cubic.

And I can already hear the response: "What?  Why?  Isn't his solution well understood?  Why yet another article?"

True, the mathematical content of the solution is well-understood.  However, the expression of that solution is not.  Girolamo Cardano (1501-1576) worked before symbolism, before even the invention of the equals sign, so any symbolic presentation of his solution misses important aspects of his thought [Note 1].  I want to think along with Cardano, to understand his solution as he did, and to bring my students to an understanding of Cardano’s world of mathematics—his ways of thinking and the mathematical tools at his disposal.  The elucidation of these points is my goal in this article.

Girolamo Cardano (1501-1576) (Source: Convergence Portrait Gallery)

Cardano, working at the very dawn of modern mathematics, drew on two mathematical traditions.  The first, a geometric tradition, started in the hundred years before Cardano’s birth, with the collection and translation of many classical Greek mathematical texts, mostly by humanists who were strong on linguistics but weak on mathematics.  During Cardano’s youth better translations, made by those skilled in both mathematics and Greek, came to market.  These translators derived proofs for those geometric theorems whose demonstrations had dropped out of the textual tradition and added new proofs for theorems whose ancient proofs were found deficient or too obscure. And so mathematical research developed, in part, out of the desire of these mathematically skilled translators to provide the genuine content of the ancient Greek texts, even if that required replacing the proofs in the (possibly corrupt) text at hand with new ones.  Cardano wrote his Ars Magna (1545) [Note 2], including his solutions to the cubic, in this charged atmosphere of the renewal of classical Greek mathematics [Note 3].

The second mathematical tradition upon which Cardano drew was the everyday world of abbaco mathematics, taught in Italian dialects to children destined to be merchants and artisans.  This was the mathematics of commerce: proportions, practical geometry and algebra up to quadratic equations, stemming ultimately from the mathematics of Islamic writers like al-Khwarizmi.  Cardano had a foot in both traditions, having learned abbaco mathematics and a little Euclid from his father [Cardano 2002, p. 126], and more Euclid as a requirement for his medical degree.  He drew heavily on both traditions in his Ars Magna, as the subject matter was algebra and the solution of equations, while the method of proof was geometric.  I argue that Cardano’s methods of discovery and indeed his way of thinking about mathematics consisted of a blend of these two traditions.

To explain the uses Cardano made of geometry and abbaco mathematics, I will examine the solution that Cardano provided to the cubic problem \(x^3=ax^2+b.\)  This exploration will uncover unfamiliar proofs, such as Cardano’s geometric depression of the cubic from \(x^3=ax^2+b\) to \(y^3=Ay+B,\) and traces of geometric and abbaco methods of discovery.  Most importantly, it will both present how Cardano worked out one of the highest achievements of pre-symbolic algebra, and bring to light part of the lost world of the abbaco master.

In working through Cardano’s mathematics, I have used pictures of cubes made from manipulatives available here at St. Cloud State University (in St. Cloud, Minnesota).  In teaching this subject, students have found that physically constructing Cardano’s three-dimensional arguments make them much easier to grasp.  This also brings home the achievement of those mathematicians after Cardano, such as Descartes, who transformed questions about cubics from solid geometry to planar curves.

Notes for Introduction

1. There are many such presentations, among which William Dunham's, in Chapter 6 of Journey through Genius, stands out.  Dunham, however, translated Cardano's demonstration into modern algebraic symbolism, and noted that "The modern reader will notice that this equation can be derived instantly by simple algebra, without recourse to the arcane geometry of cubes and slats" [p. 144].  And this is the point of the present article: to see how Cardano thought, we have to examine Cardano's recourse to cubes and slats.
2. Cardano started the Ars Magna in 1540, and it was published in 1545 by Johannes Petreius of Nuremburg.
3. See Paul Lawrence Rose, The Italian Renaissance of Mathematics, for more details.

Aspects of Abbaco Mathematics

To understand the abbaco mathematics used by Cardano, we have to step back and look at the medieval tradition of abbaco schools and their masters.  Though the subject is a fascinating and deep one, there is one particular aspect of this tradition that is crucial in the following account: abbaco masters thought in terms of canonical problems, and one particular canonical problem, the “Problem of Ten,” arises in the solution of the cubic that we will examine.

Throughout the Middle Ages and the Renaissance, city-states like Florence or Milan hired abbaco masters and established state-supported abbaco schools for children aged about nine to eleven.  Students were introduced to Hindu-Arabic numerals; the basic arithmetic operations of addition, subtraction, multiplication, and division; proportions; some practical geometry; and often algebra up to the quadratic equation.  The mathematical content was derived from Islamic texts, brought to Italy by writers such as Fibonacci.  Abbaco masters often served their cities in capacities outside of the abbaco school itself, as engineers or accountants, roles in which their mastery of abbaco mathematics made them indispensable [Note 1].

Abbaco mathematics was rhetorical—in Cardano’s time, most of the algebraic symbols with which we are so familiar were either recently invented, concurrent with the Ars Magna, or were well in the future.  For example, ‘\(+\)’ and ‘\(–\)’ were first recorded in the 1480s, and were not in common use in 1545, when the Ars Magna was published.  Robert Recorde would not invent the equals sign until 1557, and the use of letters and exponential notation would have to await Francois Viete in the 1590s and the Geometrie of Rene Descartes of 1637 [Note 2]. What Descartes would write as \(x^3=ax+b,\) Cardano wrote as “cubus aequalis rebus & numero” [Cardano 1662, Chapter 12, p. 251].

Rhetorical formulas can be difficult to remember, so algebraic rules were presented with canonical examples, which encoded the rules as algorithms within the examples.  Thus, the mind of the abbaco master was a storehouse of such canonical examples, to which he compared the new problems that he came across in his work.  When he recognized a parallel structure between the new problem and a canonical problem, he could solve the new problem by making appropriate substitutions into the canonical example.

Such canonical examples occurred even in the foundational texts of abbaco mathematics, including the Algebra of al-Khwarizmi.  An important example for us, one that occurs implicitly in Cardano’s solution to the cubic, is the “problem of ten” [Note 3].  Most abbaco texts had such problems, and one from Robert of Chester’s 1215 translation of al-Khwarizmi’s Algebra into Latin [al-Khwarizmi, p. 111] ran as follows:

Denarium numerum sic in duo diuido, vt vna parte cum altera multiplicata, productum multiplicationis in 21 terminetur. Iam ergo vnam partem, rem proponimus quam cum 10 sine re, quae alteram partem habent, multiplicamus...

In his translation of this passage into English, Louis Karpinski used \(x\) for ‘rem’ (thing), and so I offer my own translation, without symbols [Note 4]:

Ten numbers in two parts I divide in such a way, in order that one part with the other multiplied has the product of the multiplication conclude with 21. Now therefore one part we declare the thing, and then, with 10 without the thing, which the other part is, we multiply...

Al-Khwarizmi here first divided ten into two parts with product 21.  He then named the two parts, one being 'thing' and the other '10 without the thing.'  Continuing al-Khwarizmi’s solution symbolically, he distributed \(x\) over \(10-x\) to get \(10x-x^2=21.\)  By applying ‘al-jabr’ or restoration [Note 5], he transformed the latter to \(x^2+21=10x\) or, in rhetorical style, to the problem of “square and number equal to thing.”  Al-Khwarizmi had a solution for such a problem, complete with a geometric justification [al-Khwarizmi, p. 83]. Karpinski translated his solution as:

Take ½ of the unknown, that is 5, and multiply this by itself, giving 25.  From this, subtract 21, giving 4.  Take the root of this, 2, and subtract it from half of the root, leaving 3, which represents one of the parts.

The other solution is, of course, 7.  There are neither symbols nor symbolic formulas in either al-Khwarizmi’s statement of the problem, or in his solution.

The structure of the “problem of ten” was that of a number \(a\) broken into two parts \(x\) and \(y,\) with a condition on the parts; symbolically: \[x+y=a\,\,{\rm and}\,\,f(x,y)=b\] for some function \(f(x,y)\) and number \(b.\)  The usual method of solution was to express the two parts as “thing” and “number minus thing” and then to substitute into the condition, as al-Khwarizmi did above.  The “problem of ten” was canonical for quadratic problems, and served as a way to remember the rules for solving such problems.

As we shall see, Cardano’s solution to the cubic rested upon a “problem of ten.”

Notes for Aspects of Abbaco Mathematics

1. See Jens Høyrup, Jacopo da Firenze’s Tractatus Algorismi and Early Italian Abbacus Culture, for more details on abbaco mathematics and culture.  Paul Grendler, Schooling in Renaissance Italy, is also useful.
2. See Florian Cajori, A History of Mathematical Notations, for much more information about the history of mathematical symbolism.
3. The first example in Chapter 3 of the Ars Magna is an explicit working of a “problem of 10,” demonstrating Cardano’s familiarity with this problem [Cardano 1662, pp. 227-228].
4. A fairly literal translation, to catch the rhetorical style of non-symbolic algebraic writing.
5. For a discussion of the Arabic terms ‘al-jabr’ and ‘al-muqabala’, see [Katz, p. 244].

The Problem

Before we examine the solution to \(x^3=ax^2+b,\) we consider some background on the cubic.

In 1494, Luca Pacioli published his Somma di aritmetica, geometrica, proporzioni e proporzionalità, which collected much of the mathematical knowledge of the time. In his account of algebra, he listed the cubic problems, including those unsolved at the time.  He also put forth his opinion that the unsolved problems would never be solved.  Note that I write “cubic problems” rather than “cubic equations”: equations, as we know them, were a product of the hundred years after Cardano wrote, culminating with Descartes and analytic geometry.  And I use the plural, “cubic problems,” because at that time, the theory of negative numbers had not been fleshed out (Cardano called them ficta or “fictitious” in places). Thus, the cubic problems were all stated with strictly positive coefficients, and there was never a question of moving all terms to one side to achieve any kind of standard form.  What made these problems “unsolved” was the lack of a formula for the solution in terms of the numbers given in the problem; geometric solutions for some of the cubic problems had been constructed by Islamic mathematicians, such as Umar al-Khayyami’s solution of 1070 [Berggren, p. 119].

Niccolo Tartaglia (1500-1557) (Source: Convergence Portrait Gallery)

The rather dramatic story of the solution of the cubic has been told, excellently, elsewhere.  (See [Dunham, pp. 133-142] or [Katz, pp. 358-361], for example.)  In brief, Scipione del Ferro, a professor at Bologna, found the solution to "cube and thing equal to number" (in our symbolic notation, \(x^3=ax+b\) with \(a\) and \(b\) positive rational numbers) in the early sixteenth century.  He told his student Antonio Maria Fior of the solution, and Fior challenged Niccolo Tartaglia to a mathematical duel.  In such a duel, each contestant posed a list of questions to the other, with the loser paying the winner a prize.  Tartaglia had found the solution to "cube and square equal to number," and, just in time, the solution to "cube equal to thing and number." Fior couldn’t answer Tartaglia's questions, and Tartaglia won the duel.  A few years later, Cardano obtained the solution to both cubics from Tartaglia (whether or not such obtaining was underhanded is still a matter of contention), and published the solutions in his Ars Magna.

The solution I will present is to the problem “cube equal to square and number,” or \(x^3=ax^2+b.\)  Cardano’s solution in the Ars Magna proceeds in three steps over three chapters.  First, in Chapter 6, Cardano decomposed the cube into eight parts, establishing a geometric demonstration for our binomial formula \[{(x+y)}^3=x^3+3x^2y+3xy^2+y^3.\]He used this decomposition in almost all of his arguments about cubics.  Second, in Chapter 14, Cardano depressed the problem “cube equal to square and number” to “cube equal to thing and number”: symbolically, he depressed \(x^3=ax^2+b\) to \(y^3=Ay+B.\)  His geometric procedure was radically different from our analytic one, and relied on the decomposition of the cube from Chapter 6.  This depression allowed him to use his solution to “cube equal to thing and number” presented in Chapter 12, to derive his rule for the solution to “cube equal to square and number.”

His solution in Ars Magna to "cube equal to thing and number" consists of two parts, a geometric demonstration that a particular number is the solution, and a rule for finding that number from the coefficients of the problem.  The demonstration does not show how to find the number given by the rule; I argue that the number arises naturally from an abbaco "problem of ten," and that Cardano relied on this abbaco knowledge to connect his demonstration with his rule.

Decomposing a Cube

In Chapter 6 of the Ars Magna, Cardano presented his decomposition of the cube.  Symbolically, this is the familiar \({(x+y)}^3=x^3+3x^2y+3xy^2+y^3,\) but since Cardano wrote before the invention of algebraic symbolism, his presentation was geometric.  This presentation was not new with Cardano; it occurred in Fibonacci’s Liber Abaci [Fibonacci, p. 520], a copy of which Cardano had examined in Venice.

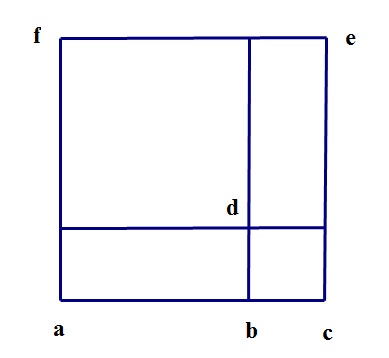
Figure 1. Cardano's figure for cubes.

Figure 1 is my replication of Cardano’s figure in Chapter 12 of the Ars Magna.  His figures were all two-dimensional, and his notation for solids and surfaces followed the notation in the diagram.  Diagonally opposed points labeled solids and surfaces, as the "cube ae" or the "square ae," and squares and cubes were often referred to by their edges, as “the cube on ac” or “the square on bc.”  This figure, then, is the base of a cube, and the line ac does double duty, as an edge of the base and also as the height of the cube.

Breaking the edge ac at the point b triggers the decomposition.  This breaks the base into four pieces, as in the figure, while the height ac is broken into two parts, the two line segments ab and bc.  Cardano then multiplied each of the four pieces of the base by the two line segments ab and bc, resulting in eight solids.  He described the resulting decomposition as [Cardano 1662, p. 251, my translation]:

... the cubes ab and bc, and thrice ab multiplied by the square on bc, and thrice bc multiplied by the square on ab.

The two pictures below present the result.

Figure 2. A cube, with top surface labeled as in Cardano’s diagram.

Figure 3. The cube decomposed.

In Figure 2 above is a cube, marked with Cardano's notation from the image in Chapter 6.  In Figure 3 is the same cube, decomposed into its eight pieces.  Of course, these are pictures of a particular cube, one with edges of nine units.  But the method Cardano described is completely general, and so this particular example stands for all.  Cardano's skillful manipulations of the decomposed cube were central to his demonstrations of the solutions to the various cubic problems.

Depressing the Cubic

The problem Cardano set himself in Chapter 14 of the Ars Magna is [Cardano 1662, p. 253]:

Let, therefore, the cube ae, in the figure of Chapter 12, equal six times the square on ac and 100.

Symbolically, this is  \(x^3=6x^2+100.\)

Cardano first reduced the problem to “cube equal to thing and number,” whose solution he had presented earlier in Chapter 12.  This reduction, or  “depressing the cubic,” transforms the equation \(x^3=6x^2+100\) to \(y^3=12y+116,\) where \(x\) and \(y\) are related by \(x=y+2.\)  In these modern times, students often see this transformation in calculus, in which the function \(f(x)=ax^3+bx^2+cx+d\) is translated by the substitution \(x\rightarrow{x-\frac{b}{3a}},\) moving the unique inflection point of \(f(x)\) to the origin and resulting in a function \(g(x)=ax^3+Cx+D\) with no quadratic term.  Cardano achieved this geometrically, as follows.

Figure 4. The cube ae.

Figure 5. A solid with same base as the cube ae, but height 6.

Figure 4 presents the cube ae, and Figure 5 presents a solid with the same base as the cube but a height of six.  As mentioned before, these particular physical solids have specific sizes, but they are meant to stand for the general case.  Here, the cube ae has an unknown side-length ac, while the solid in Figure 5 has the same (unknown) base, but a known height of six units.  Hence, the volume of the cube ae is (ac)³ and the solid in Figure 5 has volume 6(ac)², where ac is the unknown side-length.  Equating the solids in these two pictures gives us the equation \(x^3=6x^2.\)  Since, in the depression of \(x^3=ax^2+b\) to \(y^3=Ay+B,\) the number \(b\) is not geometrically manipulated, I leave it out of the pictures.

So how did Cardano perform this depression?  Starting with the cube ae, he decomposed it into eight solids by cutting the side ac at a point b, as described in the previous section. The point b is arbitrary, although in these pictures I had to choose a specific place to locate it.  The eight solids can be regrouped into four solids, as shown in Figures 6 and 7.  The original unknown, the edge ac\(=x,\) was represented in Figure 4 above by the edge of the cube.  The new unknown of the depressed equation, the edge ab\(=y,\) is the edge of the green cube in both Figure 6 and Figure 7.

Figure 6. The basic decomposed cube.

Figure 7. The decomposed cube regrouped for depressing the cube.

As seen in Figure 7, two of the four solids are the green cube on ab and the red cube on bc.  The three blue solids in Figure 6 can be stacked, giving a solid whose base is the square on ab and whose height is thrice bc, and so the blue solid in Figure 7 has volume 3(ab)²(bc).  Likewise, the three pink solids can be combined, giving a solid of volume 3(ab)(bc)².

The solid of volume 6(ac)² is also decomposed by breaking the side ac at the point b.  The decomposition can be regrouped into three solids, as shown in Figure 9.

Figure 8. The solid with height 6.

Figure 9. The solid with height 6 decomposed.

The blue solid has base (ab)² and height 6, and the red solid has base (bc)² and height 6.  The two pink solids can be combined to yield a solid of volume twice 6(ab)(bc), or 12(ab)(bc).

Up to this point the cut at b has been arbitrary.  Cardano asked, where does this cut have to be so that the solids in Figures 4 and 5 whose bases are the square on ab have the same volume?  In our pictures, this means determining the location of b so that the blue solids in Figures 7 and 9 have the same volume.  In the cube ae, the blue solid has volume 3(ab)²(bc), while the other solid produces a blue solid of volume 6(ab)².  For these to be equal, we need 3(bc) = 6, or bc = 2.  Once this had been determined, Cardano simplified the problem by eliminating solids with the same volume from each side.

Figure 10. The decomposed cube ae.

Figure 11. The decomposed solid of height 6.

The two blue solids in Figures 10 and 11, by choice of b, have the same volume, and so they cancel each other.  Given bc = 2, the pink solid in Figure 11 has twice the volume of the pink solid in Figure 10, while the red solid in Figure 11 has volume thrice that of the red solid in Figure 10.  Cancelling the common volumes gives us Figure 12.

Figure 12. What's left after cancellation.

We have the green cube on ab on the left side, while the right side consists of a pink solid of volume 12(ab) and a red solid of volume 16.  Since we have set \(y\) to be the length ab, symbolically we have \(y^3=12y+16.\)  To return to Cardano’s original problem, we add back in the number \(b=100,\) ending with \(y^3=12y+116.\)

Cardano’s method of depressing the cubic provides a good illustration of some aspects of abbaco mathematics.  This demonstration is presented as a canonical problem, one with specific coefficients.  The method, however, is completely general, and Cardano explicitly stated the key step, that “bc is one third the coefficient of \(x^2.\)”  This demonstration is canonical for problems of the type “cube equal to square and number,” with any positive coefficients whatsoever.  Just as the physical solids in the pictures stand for general solids, so too the equation \(x^3=6x^2+100\) stands for the general equation \(x^3=ax^2+b.\)

Solving the Cubic

Having depressed \(x^3=6x^2+100\) to \(y^3=12y+116,\) we now move to Chapter 12, where Cardano took up the solution to “cube equal to thing and number.”  This chapter, like many of his chapters, contains a geometric demonstration, a rule, and several examples.  Oddly, perhaps, his demonstration and his rule are seemingly unconnected: the demonstration shows that a particular number is the solution to the cubic problem but does not show how to find that number, while the rule provides an algorithm to find directly the solution in terms of the coefficients, without reference to the number produced by the demonstration. The bridge between the demonstration and the rule, which Cardano left implicit, is an abbaco “rule of ten” problem.

Taking up the demonstration first, Cardano showed that, if ab and bc satisfy the relations (ab)³ + (bc)³ \(=b\) and 3(ab)(bc) \(=a,\) then the solution ac of the original problem (ac)³ \(=a\)(ac) \(+\,b\) is the sum of ab and bc.  His demonstration rested on a manipulation of the decomposition of the cube presented above.  In Figure 2, we have the cube with edge ac.  By cutting it at b, we get the usual decomposition presented in Figures 2 and 3.  Cardano then arranged the solids of the decomposition as in Figure 13.  The green cube with edge ab and the red cube with edge bc are grouped together, while the pink and blue solids are grouped into three solids with edges ab, bc, and ab + bc = ac.

Figure 13. The cube ae decomposed for solving a cubic (compare with Figures 6 and 7 on preceding page).

The original problem, symbolically \(y^3=12y+116,\) is represented geometrically by

(ac)³ = 12(ac) + 116

or, decomposing the cube of volume (ac)³ as in Figure 13, by

(ab)³ + (bc)³ + 3(ab)(bc)(ac) = 12(ac) + 116.

The term (ab)³ + (bc)³ is represented by the green cube and the red cube, while the term 3(ab)(bc)(ac) is represented by the three pink and blue volumes.  Matching coefficients yields these two equations:

(ab)³ + (bc)³ = 116

3(ab)(bc) = 12

All this leaves the location of the cut at b undetermined.  If this cut can be determined, then ac = ab + bc is the solution of the problem.  But Cardano ended his demonstration here, and moved directly to the following rule for the solution (as translated by T. Richard Witmer in [Cardano 1993, p. 103]):

When the cube of one-third the coefficient of x is not greater than the square of one-half the constant of the equation, subtract the former from the latter and add the square root of the remainder to one-half the constant of the equation and, again, subtract it from the same half, and you will have, as was said, a binomium and its apotome, the sum of the cube roots of which constitutes the value of x.

Buried in this rule are ab and bc: one is the binomium and one is the apotome [Note 1].  But how did Cardano get from his demonstration to the rule?

The bridge, I believe, was provided by the abbaco master Cardano’s recognition that the problem resulting from the matching of coefficients above is a “problem of ten.”  Cardano nowhere in the Ars Magna explicitly provided a solution for this specific problem.  But, re-written as

(ab)³ + (bc)³ \(=b\)

(ab)³ (bc)³ \(={{\left({\frac{a}{3}}\right)}^3},\)

this is a “problem of ten” identical in form to the problem from Al-Khwarizmi discussed earlier.  Following the same method of solution, Cardano would have arrived at \[({\rm{\bf ab}})^6+{\left({\frac{a}{3}}\right)^3=b({\rm{\bf ab}})^3},\] an equation he recognized as a disguised \(x^2+B=Ax\) [Note 2].  Solving this equation for (ab)³ gave the usual two solutions from the quadratic equation, the binomium and its apotome.  Hence, the sum of the cube roots of the apotome and the binomium gave the solution to the original cubic, as his rule stated.  Contained in his rule is the restriction that \[{\left({\frac{a}{3}}\right)^3}\le{{\left({\frac{b}{2}}\right)}^2};\]this is the requirement that the discriminant of this quadratic be non-negative.  This explicit recognition of the quadratic nature of the problem supports the idea that Cardano solved it as a “problem of ten.”

Notes for Solving the Cubic

1. A binomium is a term of the form \(a+{\sqrt b};\) its apotome is its conjugate \(a-{\sqrt b}.\)  They arise naturally in the solution of quadratic equations.
2. In Chapter 2 of the Ars Magna [Cardano 1662, pp. 226-227], Cardano listed both \(x^4+B=Ax^2\) and \(x^6+B=Ax^3\) as derivative cases of \(x^2+B=Ax.\)

Conclusion

As our excursion through Cardano’s solution to “cube equal to square and number” comes to a close, let us reflect on what we’ve just seen.

First, the abbaco ways of thinking provided an important element of the solution.  Both Cardano and Tartaglia were trained in abbaco techniques, and their ability to draw on their stores of canonical problems helped them recognize a “problem of ten” in a geometric context.

Second, Cardano’s mastery of the decomposition of the cube and how the resulting solids could be arranged showed up in two places.  The recognition that a solid of volume (ab)(bc)² and one of volume (ab)²(bc) can be put together to give one solid of volume (ab)(bc)(ac) (where ac = ab + bc) was essential in creating the geometric situation in which he could see the “problem of ten.”  But this mastery also showed itself in the geometric depression of the cubic, a tour-de-force of solid geometry.  Recognizing that the cut at b in the side ac of the cube on ac can be specified to make two of the squared terms cancel each other out, and that this specification results in a problem having only a cubic term and a linear term, reveals an ability to move between geometric and abbaco thinking, a certain linking of geometry and rhetorical algebra.

As a teacher of mathematics and of history of mathematics, I find that this episode connects well with my students.  They see a different method of depressing the cubic, one tied to solving a cubic equation rather than shifting the graph of a function.  The geometry involved is solid geometry, neither the planar geometry so often emphasized in history of mathematics courses, nor the analytic geometry of calculus.  This episode serves to illustrate the heights to which abbaco mathematics could rise, and the difficulty of doing algebra without symbolism, whetting students’ appetites for Viete, Thomas Harriot, and Descartes.  

After all, this episode in the history of mathematics is both an ending and a beginning.  The time of the abbaco master was coming to an end, as the discovery of the Arithmetica of Diophantus and the algebraic symbolism of Viete changed the ways of thinking about algebra.  But the time of what we would call “research mathematics” was just beginning, and Cardano’s solutions of the cubics, solutions that had escaped the ancients, were among the first new discoveries about pure mathematics in Western Europe in a long time.  The solutions of the cubics bolstered the confidence of other mathematicians that they could, indeed, go beyond the Greeks.

The Ars Magna, then, is both the glorious pinnacle of a dying tradition (the rhetorical algebra of the abbaco tradition) and a first baby step in the tradition then just beginning (the study of polynomial equations, and indeed that of modern mathematics). Cardano and his compeers Tartaglia and Lodovico Ferrari found these solutions using a mixture of both abbaco reasoning and geometric reasoning.  Both were helpful; indeed, both were necessary.

Acknowledgements

I thank Kate Gill, Jeff Mullins, Judy Dorn and especially Steve Walk (all of St. Cloud State University) for their close readings of and insightful comments on various drafts of this paper.  I greatly appreciate Janet Beery’s close reading of this manuscript, and the comments of an anonymous reviewer.

About the Author

Bill Branson graduated from the University of California, Berkeley, with a B.A. in mathematics in 1991, and was awarded a Ph.D. in mathematics by the University of Illinois at Urbana-Champaign in 2000, with a thesis on complex differential equations.  He has been teaching at St. Cloud State University in St. Cloud, Minnesota, since 2002, and during that time has shifted interest to history of mathematics, especially cultural aspects of Renaissance mathematics.  When not ploughing through Cardano's collected works, he can be found out on one of the many disc golf courses in the St. Cloud area (yes, even in winter!) or in the kitchen, cooking up dishes with vegetables and herbs from the garden he maintains with his partner Kate.

Above: The author, Bill Branson, on a recent visit to Athens, Greece

References

al-Khwarizmi and Robert of Chester, Robert of Chester’s Latin Translation of the Algebra of Al-Khowarizmi, translated by Louis Charles Karpinski, 1915, London: MacMillan and Company Limited.

Berggren, J.L., Episodes in the Mathematics of Medieval Islam, 1986, New York: Springer-Verlag.

Cajori, Florian.  A History of Mathematical Notations, 1993, New York: Dover Publications.  Originally published by Open Court, 1928.

Cardano, Girolamo, Artis Magnae, sive De Regulis Algebraicis, in Opera Omnia, Vol. 4 (pp. 221-302), 1662, Leiden.
Available at http://filolinux.dipafilo.unimi.it/cardano/testi/opera.html.

Cardano, Girolamo, Ars Magna or the Rules of Algebra, translated by T. Richard Witmer, 1993, New York: Dover Publications.  Originally published by MIT Press, 1968.

Cardano, Girolamo, The Book of My Life, translated by Jean Stoner, 2002, New York: New York Review of Books.

Dunham, William.  Journey through Genius, 1991, Penguin Books: New York. Originally published by John Wiley & Sons, 1990.

Fibonacci, Leonardo, Fibonacci’s Liber Abaci: Leonardo Pisano’s Book of Calculation, translated by L. E. Sigler, 2002, New York: Springer-Verlag.

Grendler, Paul F, Schooling in Renaissance Italy, 1989, Baltimore and London: The Johns Hopkins University Press.

Høyrup, Jens, Jacopo da Firenze’s Tractatus Algorismi and Early Italian Abbacus Culture, 2007, Basel-Boston-Berlin: Birkhäuser Verlag AG.

Katz, Victor J., A History of Mathematics: An Introduction (2nd edition), 1998, Reading MA: Addison-Wesley.

Rose, Paul Lawrence, The Italian Renaissance of Mathematics, 1975, Genève: Librairie Droz.