The students and I arrived in Italy in late May to study the history of mathematics as it relates to Renaissance art and architecture. On our first full day, we climbed to the top of the Cathedral of Santa Maria del Fiore to see how Fillipo Brunelleschi used geometry to construct the impressive dome. We were among the first people to climb the dome that Tuscan morning, and our group discussion at the top was a memorable way to begin our tour.

Figure 2: Enthusiastic about the history of mathematics at Santa Maria del Fiore in Florence. Photo by the author.

In fact, we attracted a crowd. This happened throughout our travels; at the top of the Duomo in Florence, while we discussed the place of geometry in architecture, several strangers stopped to listen. I stifled a laugh as a woman near me elbowed her husband and muttered, “Pay attention, Henry.” Everywhere, people are thirsty for knowledge.

The nearby Duomo Museum contains the original “Gates of Paradise” by Lorenzo Ghiberti, which is a masterpiece of three-dimensional representation in bronze. The museum also contains works by Donatello and Michelangelo, as well as a recently discovered “practice dome” by Brunelleschi. In the same piazza is the Baptistery of St. John, a celebration of symmetry that Brunelleschi used to demonstrate the power of linear perspective in painting.

Another highlight of our time in Florence was the Accademia museum, home of Michelangelo’s "David", as well as his "Prisoners".

Figure 3: One of Michelangelo's "Prisoners”. Wikipedia.

Michelangelo claimed that his sculptures existed within the marble itself, and that his job was to reveal the hidden creatures. For my students, these "Prisoners" sparked a lively conversation about Platonism and mathematics. The excitement was enhanced by the fact that I had neglected to obtain appropriate permissions to “lecture” inside the Accademia[1]

Serendipity

One afternoon, I led the students on a “history of mathematics walking tour” of old-town Florence. Rain clouds gathered as we began, and by the time we reached the Orsanmichele Church, it was raining hard. One of the striking features of that church is the set of fourteen architectural niches on its external walls. One niche is occupied by Donatello’s statue of St. Mark, believed to be the first explicit use of trigonometry in a free-standing statue since ancient times. Donatello computed the exact proportions necessary to make the statue appear realistic when viewed from below (e.g., at street level). According to the story, when the statue was first presented to the wool guild that paid for it, the guild members were underwhelmed by its “inappropriate” proportions. But when the statue was finally lifted into its niche, the importance of trigonometry in sculpture was revealed.

Figure 4: “St. Mark” by Donatello (1413). Wikipedia.

I tried to explain all of this wonderful history in a downpour, as the students made a “roof” of umbrellas over our heads. Eventually the rain forced us inside the church. I had not planned to go inside, but took advantage of the cool, dimly-lit setting to tell the story of Savonarola and the end of the Florentine Renaissance. The ambiance was perfect for a horror story, and the students also had a chance to see a fine example of a Gothic church. In a final twist, we were observed by a local tour guide who had her own group in the church at that same time. She gave us a private tour of the Uffizi Gallery the following day—a neat connection enhanced by a rainstorm.

A note on guided tours

I was hesitant about taking the students to the Uffizi because of the crowds, but the opportunity to trace the development of linear perspective in Renaissance art was not to be missed. Highlights (depending on one's perspective) included “St. Francis Receiving the Stigmata” by della Croce, “The Battle of San Romano” by Uccello, and “Triumph” by della Francesca. Our experience at the Uffizi supports the argument that paying to hire a local guide is money well spent. Our guide had the perfect mix of knowledge, passion, and humor. She really brought mathematics to life through art, and engaged the students with plenty of questions. We paid for guides throughout our tour of Europe (many arranged ahead of time), and each one greatly enhanced our experience. In terms of cost, our tour of the Uffizi was the most expensive, about $17 per student—a good value for a 2.5-hour tour with an expert.

Day Trips from Florence

Florence is within an easy train ride of several interesting cities. We spent a day in Pisa, and another in Bologna.

Pisa is a city that both Leonardo of Pisa (Fibonacci) and Galileo called home at different times in their lives. Our discussions in Pisa centered on the importance of trading ports in bringing knowledge from the Islamic Empire into Western Europe. From the top of the Leaning Tower (remarkably uncrowded in May), we talked about the history of numerals. From the Camposanto Monumentale, in front of the monument to Fibonacci, we discussed phi, phyllotaxis, and the Fibonacci sequence. Ever since taking a history of mathematics course as an undergraduate, I wanted to teach those ideas to students in Pisa, at Fibonacc's monumenti. It was a powerful moment. We also visited the cathedral where (perhaps apocryphally) Galileo was inspired to study pendulums by the swinging of a chandelier (which still swings to this day).

We rambled through the medieval streets of Pisa, thinking about Hindu-Arabic numerals and algebra. We sat at the feet of the statue of Fibonacci in the Camposanto Monumentale and worked problems from Liber Abaci on a portable whiteboard we’d carried with us from home. We discussed the meaning of such problems to a 13th-century merchant. We explored the fascinating properties of the Fibonacci sequence and spirals. Other tourists watched us with curiosity. A woman took out her phone and snapped a picture of the Americans working math problems in a cemetery.

Figure 5. Paying homage at the monument to Fibonacci in Pisa. Photo by the author.

Two days later, the students and I fell in love with Bologna. It is a charming university town, with a laid-back atmosphere that is completely different from Florence. The university is connected with the solution of the cubic equation, and with well-known characters such as Cardano, Tartaglia, and del Ferro. Bologna was also the home of Bonaventura Cavalieri who did foundational work with the geometry of indivisibles. The account of his work, and the persecution he suffered at the hands of the Catholic Church, comprise several thought-provoking chapters in the book Infinitesimal by Amir Alexander.

Serendipity Lost

While in Bologna, we visited Santa Maria della Mascarella, the church connected with Cavalieri. As the students and I discussed infinitesimals on the sidewalk, a priest from the church came outside and asked (in Italian) if we were Catholics, or tourists. I speak very little Italian, and tried to tell him we were mathematicians.  He became very excited, and pointed to a plaque honoring Cavalieri on the wall of his church. He spoke at length, and with passion. We listened in awe, not understanding a single word. In the end, we all thanked him. He smiled, gave a little wave, got into his tiny Italian car and drove away. But what did he say? What knowledge of Cavalieri and the geometry of indivisibles was he trying to impart? This is the curse of being a monolingual American.

Figure 6: Plaque honoring Bonaventura Cavalieri in Bologna. Photo by the author.

The intellectual persecution of Galileo, Cavalieri, and others at the hands of the church was partly responsible for a shift in the center of mathematics from the Piazzas of Italy to the cafés of Paris and the coffee houses of London. Likewise, our group followed the footsteps of Giuseppe Lodovico Lagrangia (Joseph-Louis Lagrange) to Paris. Our time in Paris centered on three eras: the life and times of Rene Descartes, the Enlightenment, and the Romantic Age. While a few papers exist describing some of the mathematical highlights of Paris (e.g. Smith, 1923), our community would be well-served by a thorough and definitive written description of such places.

Some of the mathematical highlights of Paris coincide with tourist highlights: The Eiffel Tower features the names of 72 French scientists and mathematicians whose work led to the construction of the tower. Among the names not listed is Sophie Germain. The hour-long wait to climb the tower afforded us a great opportunity to begin a discussion on the role of women in mathematics throughout history.

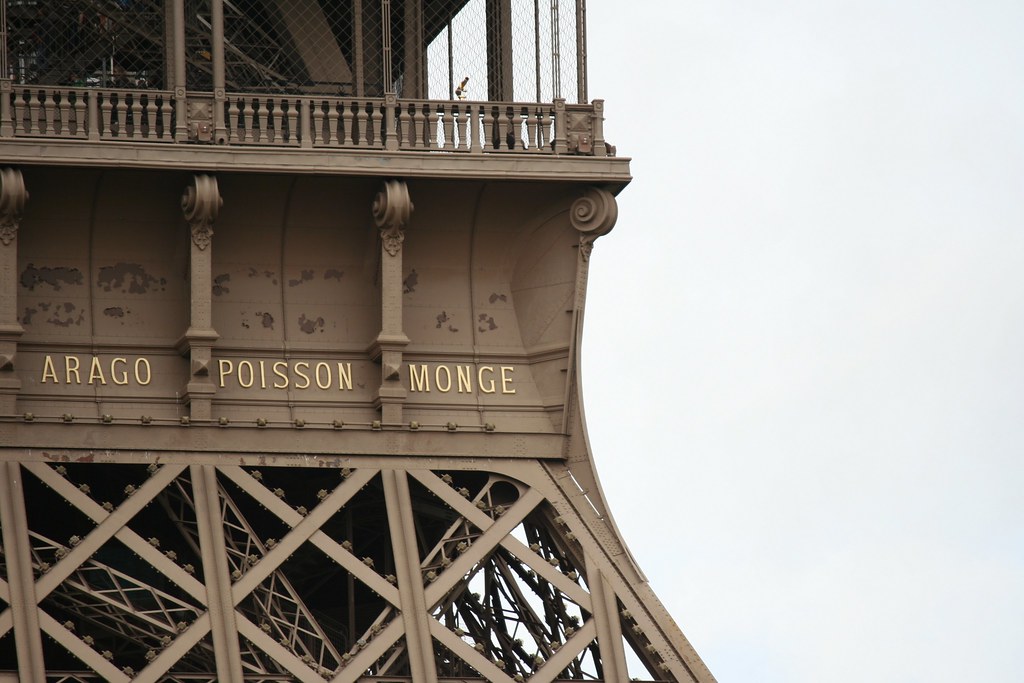
Figure 7: Three of the seventy-two names on the Eiffel Tower. Photo by Victor Ruiz, labeled for reuse under the Creative Commons License.

The oldest church in Paris, Saint-Germain-des-Prés, holds the tomb of Rene Descartes in a side chapel. The Pantheon holds the tombs of Lagrange, Monge, Condorcet, and Carnot alongside other figures such as Victor Hugo, Voltaire, and the Curies. In Napoleon’s tomb visitors find a majestic relief of the great emperor surrounded by the names of the mathematicians and scientists of his day, including Laplace, Monge, and Fourier. We sat on the steps of Napoleon’s massive tomb, with all the other tourists, and talked about the challenges and responsibilities of being a mathematician in times of social upheaval.

Figure 8: A student introducing us to Napoleon’s mathematicians. Photo by the author.

Even the palace at Versailles holds some mathematical secrets. During the reign of Louis XIV, gambling was a popular pastime at the palace. Louis encouraged gambling among the nobility in part because it kept them occupied and entertained while he ruled France. On a lovely June afternoon, we sat in the gardens of Versailles and worked out solutions to the “Problem of Points” on our mini-whiteboard. While the crowds gazed at the fountains, gardens, and glorious chateaux, we sprawled in the sunshine reading excerpts from letters between Pascal and Fermat. The gardens of Versailles are themselves a tour-de-force of geometric design, and the symbolism is clear: Louis XIV was not just another king, but a king whose rule over France was as much a part of the proper order of the Universe as the geometric principles on which his gardens were established.

Figure 9: A portion of the gardens at Versailles. Wikipedia.

Of course, some mathematical highlights of Paris are off the tourist radar: We visited Sophie Germain’s home, at 13 Rue de Savoie, and the house where Condorcet hid during the Reign of Terror at 15 Rue Servandoli. More than one student (and possibly even a professor) swallowed a lump in their throats as we stood outside the front door of the Parisian house where Germain died of breast cancer in 1831 and thought about the challenges she overcame throughout her life.

London is fast-paced, urban, and has four times the population of Paris. It was the biggest city many of my students had ever visited. After two weeks on the road, both the students and I were starting to feel weary. One of the joys, and realities, of travel is that it tends to give you a maximum concentration of thrills in a short amount of time.

As with Paris and Florence, we spent our time moving between major tourist attractions and out-of-the-way places few people visit. We toured the Tower of London and talked about Newton’s work as warden of the mint, as well as John Wallis’ cryptographic efforts during the English Civil War. We took a day-trip to Greenwich to think about the longitude problem, Huygens’s pendulum clock, and ponder the “Longitude problems” of our era. We climbed the dome of St. Paul’s Cathedral and discussed connections between mathematics and architecture.

We were graciously hosted at the Royal Society where we received an up-close look at some astounding manuscripts from the history of mathematics and science. I had read parts of Newton’s Principia and seen digital images online of the original first edition. At the Royal Society, we were allowed to flip through Flamsteed’s copy of the first edition, and to touch his handwritten marginal notes: the great astronomer was checking the math of the great mathematician, right before our very eyes.  “You can touch it,” our guide told us as she opened Newton’s own copy of his Principia, filled with his notes for the upcoming second edition. Newton once held that book in his own hands. Now we held it. Did any of his DNA rub off on us?

At the British Museum, we were granted behind-the-scenes access to examine rare Babylonian mathematical tablets. The opportunity to handle a 3,000-year-old mathematical tablet was breathtaking. The curator, Dr. Christopher Walker, patiently and expertly explained what is known (and what is not known) about mathematics in Old Babylon. I had taught that the Babylonians used base-60 for computations, and was surprised to find that this wasn’t always the case. Occasionally, a decimal system was employed, and one tablet is even in base-70. The shining star of the collection, however, was a tiny tablet which described the movement of Jupiter, and featured an early version of integral calculus (Cowen, 2016)!

Figure 10: Dazzled by millennia-old mathematical tablets. Photo by the author.

Day Trips from London

Taking advantage of England’s efficient and reliable train system, we spent a day in Cambridge, and another at Bletchley Park. At Cambridge, we toured Trinity College, Kings College, and the town itself. We arranged an “official tour” through the Trinity College School’s Liaison Office, and booked a tour of Cambridge town and Kings College through the Blue Badge Guides. Our time in Cambridge focused on the life and times of Newton, Hardy and Ramanujan, and Alan Turing.

Figure 11: The colonnade at Trinity College where Newton first measured the speed of sound. Photo by the author.

Dr. Nicolas Bell is the curator of the Wren Library at Trinity College, Cambridge. He graciously opened the library an hour early so that my students could spend time, in the quiet of a June morning, with Hardy and Ramanujan. He held out a timeworn sheaf of papers for us to read; it contained original letters that Ramanujan wrote from India. “Dear Mr. Hardy, I have been unwell since you saw me … .” This was the very paper he handled. The ink from his pen. Not for the first time on our trip, for a few moments in June, time travel seemed real.

On the final day of our travels, we visited Bletchley Park and the nearby National Museum of Computing. Restored to its World-War II era appearance, Bletchley Park is a truly remarkable place to visit. I was surprised by the number of hands-on activities, the poignant display of Turing’s personal effects, and the atmosphere of somber reflection that pervades the grounds. The role of mathematics in war, the persecution of people with alternative lifestyles, and the swiftness with which human beings forget the lessons of history provided a thoughtful end to our educational program.

Throughout the program, I asked students to consider the following overarching questions:

1. How have historical events and cultural ideas shaped the history of mathematics?
2. How have mathematical developments influenced history and culture?

To help answer these questions, I designed a set of readings, assignments, and site visits connected with the Florentine Renaissance, the Parisian Enlightenment and subsequent Romantic Age, the Scientific Revolution (broadly defined but with a particular focus on Galileo, Kepler, and Newton), and the 20th century.

I worked with the Education Abroad office at our University, and partnered with a logistics team in Europe to create a program that could accomplish my educational goals, while keeping the program fee at a competitive level (see Appendix 1: Fast Facts).

Hub and Spokes

All of the students completed three weeks of online modules prior to departure to Europe. The assignments were based on the following materials. Students read or watched:

• “The History of Mathematics in a Large Nutshell” (Berlinghoff and Gouvêa, 2004)
•  “The Proof” (NOVA Documentary, WGBH Video, 1997)
•  “Newton” (Gleick, 2004)

As well as selections from:

• The Scientific Revolution (Shapin, 2018)
• Dialogue and Two New Sciences by Galileo Galilei
• Mathematics in Historical Contexts (Suzuki, 2009)
• A History of Mathematics (Boyer and Mertzbach, 2011)
• Duel at Dawn (Alexander, 2010)
• Infinitesimal (Alexander, 2014)
• A Sourcebook in Mathematics (Smith, 2012)
• The Crest of the Peacock (Joseph, 1991)

Another fine resource for biographical information on female mathematicians is the Biographies of Women Mathematicians website created by Larry Riddle of Agnes Scott College.

In addition to this central “hub” of assignments, each student selected a sub-topic “spoke” of their choice. My intent was that the spokes would give the program a slightly different flavor for each student. Then, because each student brought different background knowledge to Europe, they each played the role of co-instructor at some point during our travels. Examples of spokes included:

• Mathematics and War
• Codes and Ciphers
• Mathematics and Religion
• Mathematics and Architecture
• Contributions by Minority Scholars to Mathematics
• Calculus in the 19th Century
• “Impossible” Problems
• Mathematizing the Heavens
• Women in Mathematics

After students chose a spoke, I worked with them to find a small number of additional sources beyond the hub readings. For example, the students who chose Mathematics and Architecture watched the NOVA documentary “The Great Cathedral Mystery”, read “Are There Connections Between the Mathematical Thought and Architecture of Sir Christopher Wren?” by Maria Zack (2006), and also read “Architecture, Patterns, and Mathematics” by Nikos Salingaros (1999). When we visited St. Paul’s in London, those students were well-prepared to help our entire group better understand and appreciate that space.

Assignments While Abroad

While abroad, I placed only modest expectations on the students to complete written academic work. Each student was responsible for researching one of our sites, and giving the group an introduction to that site. The students also completed a small set of “notebook assignments” associated with each site (see Appendix 2). These were questions meant to help students get more meaning from each site visit. Some notebook assignments asked students to look for certain objects—like a mathematical scavenger hunt. Others asked the students to reflect on buildings, spaces, people, or ideas. The questions were short, occasionally open-ended, and could be answered in less than 2 paragraphs. Finally, the students were responsible for updating and maintaining a daily blog of our journey (https://historyofmath.home.blog/).

Final Papers

The major assignment of the course was a paper that addressed the two overarching questions mentioned earlier. All of the pre-departure readings and notebook activities were the raw material for the students’ final papers. Crucially, I asked the students to submit a rough draft of their paper before departing to Europe. Those drafts were based on their hub assignments and flavored by their spoke assignments. While abroad, I met with each student individually to discuss their draft and provide feedback. After our time abroad, students were required to re-write their papers and produce a final draft. I asked each student to write at least one full page of reflection on how their experiences abroad led to specific changes in their understanding of mathematics. All of the students (and myself) arrived in Europe with preconceived ideas about mathematics, history, culture, and the ways they interact. In the reflection piece, students described how their ideas changed. The reflection portions of their papers were the very best thing students have written for me in any course I’ve taught.

Challenges

When we teach with historical sources at home, we make difficult decisions. I don’t give my students the original Latin text, so I have to choose a translation. At that point, they’re not reading Euler, they’re reading Blanton. How much cultural background information should I provide? How much do they need to know about Euler to appreciate his writing style? How can I assess if they’ve learned anything they wouldn’t have if I just taught a typical lesson on derivatives of trigonometric functions?

Teaching in historical places presents similar challenges: Cities evolve, buildings are torn down and new ones are erected. Artifacts are in museums, out of their original physical context, and are surrounded by other objects chosen to convey a particular message. When you visit a historical place, you’re surrounded by the ghosts of the past, but there are few tangible markers. In the Great Hall at Trinity College, today’s students eat their daily meals under the watchful eye of Henry VIII. There’s no sign to tell a visitor that this was where Hardy and Littlewood ate, and where Ramanujan could not eat, because of his diet and his faith. The casual visitor to Europe’s greatest sites is unaware of just how much mathematical history surrounds them. They can’t hear the whispers of the ghosts. My job was to help students imagine.

I am not an expert in Renaissance art, or architecture, or Enlightenment philosophy. My colleagues asked how I taught a lot of the content of the course, and I acknowledge that I’m still learning. What’s important is that I was not really the primary instructor of this program. I had a dozen co-instructors in my students, and in every city we visited I relied on local guides, professors, curators, and friends, to provide expertise. My role was to facilitate an atmosphere in which learning could occur. Some talk of being a “guide on the side” (Davis, 1994) in the classroom, and I literally was on the side (or in the back row, or even in a different part of the building) at many of the sites we visited.

A more intractable challenge facing educators is that many of us lack the resources, university support, or sizable student body to successfully design, recruit, and run an education abroad program on this scale. Nevertheless, I think that some sense of the magic we felt can be captured in or near a traditional classroom.

Thanks to Google Earth, instructors can take their students on “virtual tours” of many of the sites we visited, including the streets of Paris, and the Cathedral of Santa Maria del Fiore in Florence. Your students can see many different and beautiful views of both the inside, and dome, of the cathedral on a 3D virtual tour.

Many of Europe’s top museums have online, interactive sites where anyone can explore the mathematical properties of artistic masterpieces. With the advent of virtual reality, a visit to the Louvre or the British Museum is at your fingertips. The National Museum of Computing also has a website where users can take a virtual 3D tour, and explore a reproduction of Turing’s “Bombe” machine. The Google “Arts and Culture” project takes you to street views (and even inside) some of the most fascinating places on the planet.

Several of the primary source documents we examined have been digitized and are freely available online. Students anywhere in the world can see Edmund Halley’s handwritten notes in Newton’s Principia by visiting the website of the Royal Society. A project to digitize all of Newton’s papers at Trinity is underway at the Wren Library, including a personal notebook he kept between 1659 and 1661. Users can search the collection of the British Museum without ever setting foot in London.

“Study away” field trips can be a less expensive alternative to a traditional study abroad program. Many U.S. cities have museums dedicated to science that feature at least some mathematical components. If you are fortunate enough to live near New York City, the Museum of Mathematics could be an inspirational excursion. The Smithsonian museums in Washington, D.C., contain some excellent mathematical connections, and visitors to the Smithsonian Learning Lab can view over 5,000 mathematical items online. There are mathematical ideas represented in most large art museums. Perhaps the best collection of Islamic geometric tiles in the Western world is at the New York Metropolitan Museum of Art, and many smaller, regional museums are likely to have a number of such pieces.

There is great value in getting outside the classroom, and this value is heightened when we are able to help students “see” the mathematics in alternative spaces. For example, combine the Metropolitan Museum of Art, the Museum of Mathematics, and the architecture of New York City, and you’ve got a memorable Spring Break trip for your students!

 I can think of no better way to close this paper than to leave you with a reflection from my co-author, one of the students who lived the history of mathematics in the summer of 2019:

Most people who know me have likely heard about my discomfort surrounding the discipline of mathematics, and many were surprised when I enrolled in a study abroad program that related to the field. Admittedly, I was nervous but was ever hopeful that the benefits of the trip would outweigh any apprehension I was feeling regarding the mathematical components. In short, I’ve never been what people would describe as a “math person”. That is, of course, until I traveled half way across the world in an attempt to find some type of appreciation for the subject.

The dramatic impact that this program had on my ability to appreciate the study and practice of mathematics was something I didn’t anticipate. Following the history of mathematics from city to city, and seeing where some of the greatest mathematicians lived and worked, allowed me to see mathematics from a different perspective. I gained the ability to view mathematicians from a more realistic angle, and in turn, their discoveries began to seem much less esoteric. I felt connected to them in a way that I’m certain is unique to this program because my fellow classmates shared similar sentiments. We were able to see them as they were—real people with genuine familial, societal, and personal conflicts. I was fortunate enough to have an opportunity to participate in a program that not only discussed their mathematical studies in the context of these struggles, but placed me in the same cities where these events transpired. Without the latter element, I can say with utmost certainty that this topic would have failed to interest me in the profound way that it actually did.

Each site visit made the historical figures come alive, almost as if we were standing in the same room together. One of my favorite experiences was our tour of Bletchley Park, where Alan Turing’s office was arranged to be as historically accurate as possible. The museum curators did a phenomenal job recreating the scene, including details such as his sweater hanging in the closet and World War II propaganda posters hanging on the walls. Although past courses had touched on the significance of Turing’s bombe machine, they didn’t acknowledge the influence that society had on the code-breaking genius himself. Our summer curriculum was all encompassing, considering both the societal impact of the work carried out at Bletchley Park and the personal trials that shaped Turing’s professional career. Needless to say, it was a privilege to observe and exist in what used to be his workspace.

I will not be challenging myself with the joys of line integrals or Green’s theorem in the near future. However, I can confidently say that due to my participation in this study abroad program, I am much more aware of the intimate relationships between society and mathematical innovation. Appreciating formulas, proofs, and all of the other crazy and wonderful quirks of this discipline is no longer a difficult task—I’ve seen some astonishing feats that are the products of those discoveries and understand, to some degree, the painstaking effort that was required to realize them. This program provided many opportunities for personal and academic growth, and in so doing, proved that the field of mathematics extends far beyond the black and white numbers that we read in textbooks.

Many people from across the globe helped make this program possible. We are especially thankful to Sara Papini who guided us through the Uffizi Gallery with style and grace; to Christopher Walker of the British Museum; to Rupert Baker and Louisiane Ferier of the Royal Society; to Ellie Woods of Trinity College; and to Nicolas Bell of the Wren Library. Thanks to Tony Rodgers for an informative (and highly entertaining) walk through Cambridge

Stateside, we are indebted to Janet Barnett and George Heine who shared their detailed notes about mathematical sites in Paris; to Donna Pierce of Whitworth University and Maria Zack of Point Loma Nazarene University, whose study abroad programs in the history of mathematics inspired me to create my own; and to Rich Bellon of Michigan State University, whose History of Science in Europe course laid the groundwork for my own education abroad program. Finally, I am grateful to Heidi Meyer at Modesto Junior College, who shared wisdom garnered from her own mathematical history pilgrimages to Europe. I trust I can repay all this kindness by helping others who wish to carry on such work.

Finally, we wish to thank the reviewers and editors of Convergence who provided thoughtful, clear, and constructive feedback on our manuscript as well as for their encouragement.

If you have questions or would like to talk with me about designing study abroad opportunities in math history, please write to aedwards@msu.edu. I would be happy to share syllabi, assignments, rubrics, and general encouragement.

Alexander, A. R. (2010). Duel at Dawn: Heroes, martyrs, and the rise of modern mathematics. Harvard University Press.

Alexander, A. R. (2014). Infinitesimal: How a dangerous mathematical theory shaped the modern world. Oneworld Publications.

Berlinghoff, W. P., & Gouvêa, F. Q. (2004). Math through the ages: A gentle history for teachers and others. Mathematical Association of America.

Boyer, C. B., & Merzbach, U. C. (2011). A history of mathematics. 3rd ed. John Wiley & Sons.

Cowen, R. (2016). Ancient Babylonians Took First Steps to Calculus. Science, 351(6272), 435.

Davis, R. (1994). What Mathematics Should Students Learn? Journal of Mathematical Behavior, 13, 3–33.

Galilei, G. (2008). The Essential Galileo. Hackett Publishing.

Gleick, J. (2004). Isaac Newton. Vintage Books.

Joseph, G. (1991). The Crest of the Peacock. Princeton University Press.

Murdock, D. (Writer, Director and Producer). Nova: The Great Cathedral Mystery. 41(05), February 12, 2014. WGBH Video, Boston, MA.

Riddle, L. (1995). Biographies of Women Mathematicians.

Salingaros, N. (1999). Architecture, Patterns, and Mathematics, Nexus Network Journal, I, 75–85.

Shapin, S. (2018). The Scientific Revolution. University of Chicago Press.

Singh, S. (Producer). Nova: The Proof. 24(10), October 28, 1997. WGBH Video, Boston, MA.

Smith, D. E. (2012). A Source Book in Mathematics. Courier Corporation.

Suzuki, J. (2009). Mathematics in Historical Contexts. The Mathematical Association of America: Washington, DC.

Zack, M. (2006). Are There Connections Between the Mathematical Thought and Architecture of Sir Christopher Wren? In Nexus VI: Architecture and Mathematics, eds. Sylvie Duvernoy and Orietta Pedemonte, 71–81. Turin: Kim Williams Books.

Abe Edwards (aedwards@msu.edu) is a mathematician and historian of mathematics at the Lyman Briggs College within Michigan State University. He works alongside a unique mix of mathematicians, physicists, chemists, biologists, historians, philosophers, and sociologists to help bridge the sciences and humanities through interdisciplinary teaching and research. His own research explores the influences of culture, society, and history on mathematical developments. He enjoys teaching from primary historical documents, and leads a study abroad program in the history of mathematics.

Marie Savoie is a Biomedical Laboratory Diagnostics major at Michigan State University. Now in her senior year, she plans to pursue a career in medicine as a physician. The history of mathematics study abroad program gave her a new perspective on the connection between mathematics and her love of music.

Program Name: Mathematics in Historical and Social Contexts

Faculty Leader: Dr. Edwards

Offered: Summer of odd years (First 8-week session)

Structure: 8 week session: Three weeks of online preparatory work, three to four weeks abroad, one week for students to submit final papers

Eligibility: Any student who has completed their freshman year, and has passed Calculus I is welcome to apply. To apply, students must submit an unofficial transcript and a one-page essay responding to the following prompts:

• How does studying the history of mathematics support your academic and/or personal intellectual goals?
• Describe a time in your life when you suddenly had to adapt to changing circumstances, and how you handled that situation.
• Think of a community that you belong to (club, sports team, church group, family, etc.). What do you do to make other people in that group feel valued?

Credits: Students earn between 6 (minimum) and 8 (maximum) semester hour credits by enrolling in a combination of the following courses:

• MTH 490: Directed Studies in Mathematics (4 credits)
• LB 492: Senior Seminar (4 credits)
• LB 323: Science in a Global Context (4 credits)
• LB 494: Undergraduate Research (2 credits)

Lodging: Students are housed in shared hotel rooms in Florence and Paris, and in shared apartments in London. All housing is within the city center. Breakfast is provided each day, as well as some dinners.

Transportation: The program fee includes all transportation within Europe (train and bus tickets, metro passes, etc.) Students are responsible for arranging their own flights to/from the U.S., but are encouraged to book through the University’s travel agency. There is a “recommended” flight that Dr. Edwards will take, but you are not required to take that flight.

Communication: While abroad, we will use the “GroupMe” app to stay in contact with each other. A strict “buddy system” will be in force throughout the trip.

Program Fee: Approximately $3600. Education abroad scholarships are available to help reduce the program fee. Financial aid may also be used. Contact the Office of Financial Aid for more information.

Quotes                                                                                                                                                       

 “There are only two kinds of certain knowledge: Awareness of our own existence and the truths of mathematics.”

• Jean le Rond d’Alembert

“Any institution which does not suppose the people good, and the magistrate corruptible, is evil.”

• Maximillian Robespierre

“It matters little who first arrives at an idea, rather what is significant is how far that idea can go.”

• Sophie Germain

Agenda                                                                                                                                                                      .

1. (8:45 a.m.) Depart our hotel
2. (9:30 a.m.) Pantheon
   1. Student presentation
   2. One-hour audio tour
   3. Visit the crypt to hang out with some famous Enlightenment thinkers and mathematicians.
3. (11:00) Two homes of mathematical importance:
   1.  Sophie Germain’s House (13 Rue de Savoie)
   2. Condorcet’s hideout (15 Rue Servandoli)
4. (12:00) Lunch Break
5. (2:00 p.m.) Conciergerie tour

Introduction                                                                                                                                                                     .

A convenient starting point for the Enlightenment in France is the death of Louis XIV in 1715, and le Siècle des Lumières (Century of Light) came to a violent end with the French Revolution of 1789. During the Enlightenment, reason became the primary source of authority and legitimacy, leading to the advance of ideas such as democratic government, separation of church and state, and the scientific method. Ideas have consequences, and the ideals of the Enlightenment had world-wide effects. They undermined the authority of the monarchy, and led to increased questioning of the role of the church in our life.

The French Revolution profoundly influenced the history of Europe, the United States, and much of our modern-day world. It led to the world-wide decline of monarchies and the rise of democracy. It also created violent shockwaves that rippled across the globe in a series of wars and revolutions (that, in some sense, continue to this day). Some historians would rank the French Revolution as one of the pivotal events in world history. Today, we try to get just a small taste of the ideas that led to revolution, the results of the revolution, and the effects it had on the history of mathematics.

Maximillian de Robespierre was one of the architects of the Revolution. After the execution of Louis XIV in 1793, Robespierre led the Reign of Terror during which (as director of the Committee on Public Safety) he condemned thousands of French people (including the mathematicians Condorcet and Fourier) to execution for not being “sufficiently liberal” (though both Condorcet and Fourier escaped the guillotine—in different ways … .)

During the Reign of Terror, a young woman named Sophie Germain remained hidden in her parents' house where (against her father’s wishes) she became a master mathematician, and an inspiration for generations of young women in mathematics and science. Her untimely death from breast cancer is one of the great tragedies in math history. Robespierre also experienced an untimely death. As the very committee he once led became increasingly bloodthirsty, Robespierre became a target. He was executed at the guillotine in 1794 at age 36.

The French Revolution is a complicated era that is tricky to get a handle on, and we certainly won’t get a full picture today. Our goals are to understand some of the major events, people, and places. Surprisingly, these events had important effects on the field of mathematics, and what it means to be a mathematician.

Notebook Assignments                                                                                                                                                  .

1. There are several famous mathematicians buried in the Panthéon, including Joseph-Louis Lagrange, Lazare Carnot, Marquis de Condorcet, and Gaspard Monge. Why are they buried here? What does their inclusion, along with figures such as Voltaire and Rousseau, say about mathematicians during the 18^th century?
2. What’s the connection between the French Revolution and Sophie Germain? What mathematical accomplishments is Sophie Germain known for?
3. The playwright Honore de Balzac wrote about life during the Revolution: “Life is a series of combinations, and you have to study and adapt to them if you are to succeed in maintaining a good position.” Describe some ways in which mathematicians either “adapted” or “resisted” during the French Revolution. Then answer this question: In your own life, how do you decide when to “adapt”, and when to “resist”? Take a few moments to be honest with yourself about this question.
4. (MTH 490 Students Only) Read “Selections from the Preliminary Discourse to the Encyclopedia” by Jean le Rond d’Alembert (posted online). Then answer this question: For d’Alembert, what branch of mathematics is the highest level of abstraction? Why (according to d’Alembert) should mathematicians not go beyond that point? What does this say about mathematics during the Enlightenment?