Mabel was born on February 6, 1868, on the Near West Side of Chicago to Sarah Jane (Clark) Sykes (1837–1917) and James Walter Sykes (1833–1896). Born in New Hampshire and educated in Worcester, Massachusetts, her father was the son of a woolen manufacturer. James Sykes worked in the grain industry in Boston before relocating to Chicago in 1859, where he and his business partner built Chicago’s first grain dryer [2]. Within a year he established his own firm, J.W. Sykes & Co., and married Sarah Jane Clark. Mabel was born at home eight years later, just a mile northwest of the origin of the Great Chicago Fire of 1871. Driven by strong winds, the fire came within five blocks of her place of birth. Her father’s business was not so lucky; located on LaSalle Street in the heart of the business district, “the great fire made a clean sweep of Mr. Sykes’s property, and he was unfortunate enough to be among those who recovered no insurance” [2].

James Sykes’ business and the family home both relocated around Chicago often during Mabel’s early life as she welcomed three younger siblings: Marion, Florence Winifred, and Walter James. From 1883 to 1887 she attended West Division High School, a newly established 4-year school that expanded tremendously during her time there as Chicago dealt with its ever-growing population. In her last year of high school her father’s business failed and, worse yet, the resulting seizure of Sykes’ warehouse led to his arrest for fraud in October 1886 [10]. Sykes had claimed nonexistent warehouse stock as collateral against some very large loans [15]. Though the family’s financial situation could not have been as secure as it had been prior to their father’s legal troubles, both Mabel and her sister Marion were still afforded the finest educational opportunities available for women interested in mathematics and science.

While her father’s case was proceeding through the legal system, Mabel graduated from high school and, in 1887, started her undergraduate studies at Wellesley College in Massachusetts, a top-tier women’s college with a strong program in mathematics. Tuition and board was $300 per year during Mabel’s time at Wellesley [17, 18, 19, 20]. In what must have been a devastating state of affairs for the Sykes family, her father’s case was national news, appearing on the front page of the New York Times when he received a three-year sentence in 1888. The Times summarized the Chicago courtroom scene: “Sykes took the verdict coolly, blew his nose, and received the expressions of sympathy of a group of well-dressed people who surrounded him” [6]. While this must have been a heavy weight for Mabel to bear in her first two years at Wellesley, she stayed on track with her studies and graduated in four years with a Bachelor of Science degree in 1891 [22]. Though Wellesley was among the top producers of women who continued their studies to a terminal degree, this was to be Sykes' highest degree [8]. Meanwhile, her sister Marion completed her high school education and worked as a Chicago elementary school teacher for three years. It was not until Mabel completed her degree at Wellesley that Marion continued her education [24].

Mabel began her teaching career upon receiving her bachelor’s degree from Wellesley in 1891. She did not stray too far from her alma mater, accepting a position just a few miles away at the Home School in Natick, Massachusetts. Perhaps she stayed to be near her sister, Marion, who was just starting her first year at Wellesley and with whom she would remain close for her entire life. Mabel spent only one year in Natick, where she taught classes in mathematics, Bible, German and French, before taking a mathematics position in 1892 at Alma College, a women’s college in Ontario, Canada [21, 23]. Founded in 1881, Alma was housed entirely in one building and enrolled about 80 undergraduates. Of the 20 faculty members, half specialized in music and fine arts and a quarter taught literature and languages. Mabel was the sole Mathematics and Natural Sciences faculty member [1, 3]. She spent three years in Canada before leaving to return to Chicago in 1895, the same year Marion finished her degree at Wellesley. They both secured teaching positions at a relatively new school located at what was then near the southeastern far reaches of Chicago, South Chicago High School.

This area of Chicago was feeling the effects of the burgeoning paper and steel mill industry, which was accompanied by a growing immigrant population and a need for public schools. South Chicago High School was established in 1882 to address these needs. During Mabel and Marion’s time there, the school experienced tremendous increases in its student body and several phases of building development and relocation, including a name change in 1910 to James H. Bowen High School. There were also periods of time when the school housed elementary and junior high students. Through all of these phases, Mabel always taught high-school-level mathematics, but Marion taught elementary-level science classes before transitioning to high school earth sciences in 1901 [25]. According to census records, Wellesley alumni records, the University of Chicago annual register, and the annual Chicago city directory, Mabel found student housing near the University of Chicago while Marion stayed with her parents closer to the business district in the first years after their return to Chicago. Mabel was paid $1000 per year in 1896, certainly a higher salary than Marion earned as an elementary school teacher [13]. Being in Hyde Park gave Mabel easy access to the resources of a major university, and she took graduate classes at the University of Chicago, though she did not earn another degree. Those readers familiar with Chicago might be interested to know that Mabel’s five-mile commute from Hyde Park to South Chicago would have been easily traversed with the extensive and thriving 5¢ cable car system in use until 1906.

Figure 1: Bowen High School Faculty (1912): Mabel Sykes in third row from the bottom, third from the left. Marion Sykes in second row, second from the right.

The sisters had only been home for a year when their father passed away in October 1896. Marion continued residing with her mother and her younger sister, Winifred Wikoff, during this time, and she, like her sister, did some graduate work at the University of Chicago. While Mabel continued living on her own for at least five years, by 1910 Mabel and Marion resided with their widowed mother, Sarah Jane, in Hyde Park. The two sisters continued sharing their household after Sarah Jane passed away at the end of 1917. They would spend the rest of their lives working together in the Chicago public school system and sharing a home in Hyde Park. According to statistics published by the National Education Association, the median Chicago high school teacher salary in 1919 was $1107 [5]. Census data indicates Mabel and Marion were able to afford live-in help by 1920, and thus, we assume, they led a comfortable life. Mabel was involved in her local community, where she transcribed books into braille for the Chicago Public Library and worked for Children’s Aid [24]. Marion later served as the principal of the elementary and the junior high schools in her last fourteen years at Bowen [25].

Figure 2: Bowen High School Faculty (1915): Mabel Sykes on right in front row. Marion Sykes in back row, fifth from the right.

Marion survived both of her sisters. Winifred passed away at the end of 1937 and Mabel passed away at home just a few months later on her seventieth birthday. Mabel’s obituary notes that she had been ill since shortly after her retirement in 1934 [9]. Marion retired the year after Mabel and lived another ten years after Mabel’s passing. Between the Sykes sisters there are 82 years of service to Chicago public schools, two full lives devoted to education.

In addition to her role as a teacher, Mabel Sykes was also a scholar. She authored over half a dozen mathematics books and over a dozen articles between 1903 and 1935. Her articles are primarily pedagogical in nature, and the majority of the longer works are co-authored textbooks in high school geometry and algebra. Her passion for teaching mathematics is evident through these written works. She also voiced opinions on the state of mathematics education and made suggestions for improving the teaching of geometry and algebra, in particular, or the high school curriculum, in general, based on her many years of experience in the classroom.

Figure 3: Mabel Sykes in 1923.

Sykes was an active member in the Chicago and Cook County mathematics teachers’ associations early in her career. Reports from regional meetings show that she was a vocal participant and chaired several committees [14]. She was also an active member in the Central Association of Science and Mathematics Teachers, a regional professional society that pre-dated the formation in 1920 of the National Council of Teachers of Mathematics (NCTM). She served as Secretary to the Central Association from 1905 to 1910, continuing sporadically until 1919. She served as a delegate to the national committee in 1920 and was elected Vice President of the NCTM in 1923 [11, 16, 56, 57, 59, 62, 63]. Her national committee work is especially noteworthy. As part of the larger push for mathematics education reform at the start of the twentieth century, the American Federation of Teachers of Mathematics and Natural Sciences and the National Education Association jointly commissioned a group of educators to review the high school geometry curriculum in 1908. The National Committee of Fifteen on the Geometry Syllabus consisted of seven university professors and eight high school instructors hailing from schools across the United States, with the University of Chicago’s H. E. Slaught serving as the chair. Whether it was through her publications, graduate studies at the University of Chicago, or presentations at local conferences, Sykes clearly made an impression on the organizers because she was the only woman chosen to serve on this committee [16]. (On a related note, Sykes credited Slaught for his help with her 1912 Source Book.) After four years of work, the committee proposed a new geometry syllabus that was adopted by the NEA in 1912 [7]. After her service on this committee, she chaired the regional committee for the establishment of the geometry syllabus for the Chicago public school system [60].

In her four decades as an educator, Sykes wrote over a dozen articles on the teaching of geometry, algebra, and trigonometry. A list of these articles can be found in the bibliography. Spanning over three decades, Sykes’ sustained scholarship demonstrates her lifelong passion for teaching mathematics, and her willingness to freely share her thoughts about mathematics education beyond her own classroom. A common theme in Sykes’ articles is an emphasis on intentionality in the organization and presentation of mathematics within the high school curriculum, specifically algebra and geometry. For example, she quoted a portion of an address given by John Merle Coulter (chair of the University of Chicago's Department of Botany from 1896 to 1925) in both her 1903 article, entitled “Aims and Methods in the Teaching of Plane Geometry” [27], and her 1927 article, “Some Pedagogical Aspects of Geometry Teaching” [33]. The following is from the 1927 article:

Many years ago, Dr. J. M. Coulter, the botanist, read a paper on the “Mission of Science in Education.” Something that he said in this paper has a direct application to much of our geometry teaching today. He contrasted two types of instruction in the following words: “In the one case, the facts are presented in the helter-skelter fashion, solid and substantial enough, but a regular mob, with no logical arrangement, no evolution of a controlling idea. ... In the other case fewer facts are presented, but they are the important ones, and marshalled in orderly array, battalion by battalion. They move as a great whole towards some definite object. ... Instead of a level plain, there are mountain peaks and valleys. There is a perspective: there are vistas from every point of view.”

This quote encapsulates one of Sykes’ major tenets in her philosophy of teaching. In her 1905 article, “Radical and Conservative Elements in the Teaching of Mathematics” [28], she similarly affirmed that "what is of value in any course, is the point of view, not the mass of details, which must of necessity be forgotten.” To this end, she proclaimed that “the right of the teacher to think for himself and plan his own course is a divine right.” For her this included the right to change the order of the topics in order for the students to better understand their importance.

Sykes’ ideal geometry student would have the ability to solve real-world problems and follow logical arguments. Concerning the latter, as she wrote in 1903, “the ability to stick to the subject, to answer a question directly, to make or intelligently to participate in a logical argument, are necessary even in ordinary conversation.” It is in geometry class that “the pupil gets his first and often his only clear view of the logic of argumentation.” Regarding the former, in 1905 she wrote, “This does not mean that it is necessary for the pupil to retain text-proofs longer than the few recitations that they are under discussion. The important question is: Can the pupils apply theorems and general principles in inventing proofs and solving problems?” Sykes expanded on and illustrated what she meant by this in her 1906 article, “Some Practical Applications of Elementary Geometry” [29], where we find ten examples from land surveying and mechanical drawing. We show one of these examples in the "Sykes’ 1906 Persian Arch Construction" section of this article. She returned to this theme in her 1927 article [33] where she admonished textbook authors:

Consider almost any chapter in almost any geometry text with the following questions in mind: Is there a controlling idea in this chapter? ... Has each controlling idea its fundamental theorems or definitions, and are the other theorems and exercises grouped about these fundamental facts and made subordinate to them? In other words does the careful classification of material extend beyond the mere division into chapters, down to the last detail? Is this organization so clear and evident that the pupil is conscious of it?

Clearly she approached textbook authoring with these overarching ideals and found that others were not as intentional in their choices.

Other articles moved beyond this theme as she explored college entrance examination data and the wide range of abilities students bring to the mathematics classroom. In her 1917 article, “The Case Against High School Mathematics” [31], Sykes defended high-school mathematics teachers against attacks based on the high failure rates in mathematics for college entrance exams. She suggested that mathematics had been unfairly singled out since most other subject areas had similar failure rates. She also provocatively noted, “one cannot help wondering why all of the mathematics teaching in the country should be condemned from the results of examinations that are evidently intended to exclude young people from college instead of admitting young people to college.”

In her 1932 article, “The Problem of Individual Differences in Mathematics Classes” [36], Sykes described her study that “was undertaken in connection with sabbatical leave from one of the Chicago high schools and covers over fifty schools, twenty-five of which were visited by the writer.” In this and her follow-up article, “Differentiated Assignments” [37], she detailed methods that address the variety of abilities and learning styles teachers encounter in the classroom. The “Ability Grouping” method, where students are divided into classes that move at different paces according to their perceived abilities, is called tracking today. In the “Differentiated Assignments” method, students in the same class completed different assignments. Each student was allowed to chose between four “contract” levels, A, B, C, or D, each with a different set of problems ranging from easiest (D) to most difficult (A). The “Individual Instruction” method was suggested for “slow,” “failing,” or “repeater” pupils. Given the time and labor-intensive nature of individual instruction, it is not surprising that Sykes wrote in 1932, “the crowded condition of the programs of both teachers and pupils, however, limits the possibility of such work. One city conducts classes on Saturday mornings for pupils who need help on class work or who have work to make up. Attendance is voluntary. [36]” Regarding this research, Sykes did not draw any sweeping conclusions. Instead, she concluded by noting “further study might bring to light other variations of the general plans reported” [36].

Sykes put the teaching principles espoused in her articles into practice in her books on geometry and algebra, which included A Source Book of Problems for Geometry Based upon Industrial Design and Architectural Ornament (1912), Plane Geometry (1918, 1922 and 1932), Solid Geometry (1922 and 1933), Beginner’s Algebra (1922), A Second Course in Algebra (1924), and Key to Plane Geometry (1926). All but the Source Book are textbooks co-authored with Clarence E. Comstock, a professor at Bradley Polytechnic Institute in Peoria, Illinois. Both Plane Geometry and Solid Geometry were revised in the 1930s with an added co-author, Charles M. Austin, a local high school teacher who was the first president of the NCTM. Regarding the distribution of work between Sykes and her major co-author Comstock, Sykes wrote, “I do the major work on the geometries and Mr. Comstock on the algebras. The geometries are really mine” [24].

While the co-authored books are traditional high-school textbooks, Sykes’ solo work stands apart as a singular scholarly achievement. In her 1912 Source Book of Problems for Geometry, Sykes used complex and beautiful architectural designs, in her own words in the preface, “the best in historic ornament,” as her inspiration for over 1800 exercises on proof, construction and computation techniques. To pique the reader’s interest, we highlight a few of these designs, accompanied by GeoGebra applets, in the Source Book section of this paper. Before presenting the book examples, we first review the standard Euclidean constructions and give Sykes’ 1906 construction of a Persian arch.

Before we present Sykes’ architectural constructions, it will be helpful to review some basic geometric constructions. The Euclidean tools of construction are limited to an unmarked straightedge and a compass. We can visualize the straightedge as a ruler without markings for length. The compass is the tool that allows us to construct a circle by planting one compass point while sweeping the other. We will assume that we have a rigid compass, that is, given a point, A, and a segment of length r, we can construct the circle with center \(A\) and radius \(r\). With these tools we are able perform a number of standard constructions, including:

• Constructing an equilateral triangle given a segment as a side [I.1]¹
• Bisecting a given angle [I.9]
• Bisecting a given segment [I.10]
• Constructing a perpendicular to a line from a point on the line [I.11]
• Constructing a perpendicular to a line from a point not on the line [I.12]
• Copying an angle [I.23]
• Constructing a parallel to a line from a point not on the line [I.31]
• Dividing a given segment into n equal segments [VI.9]

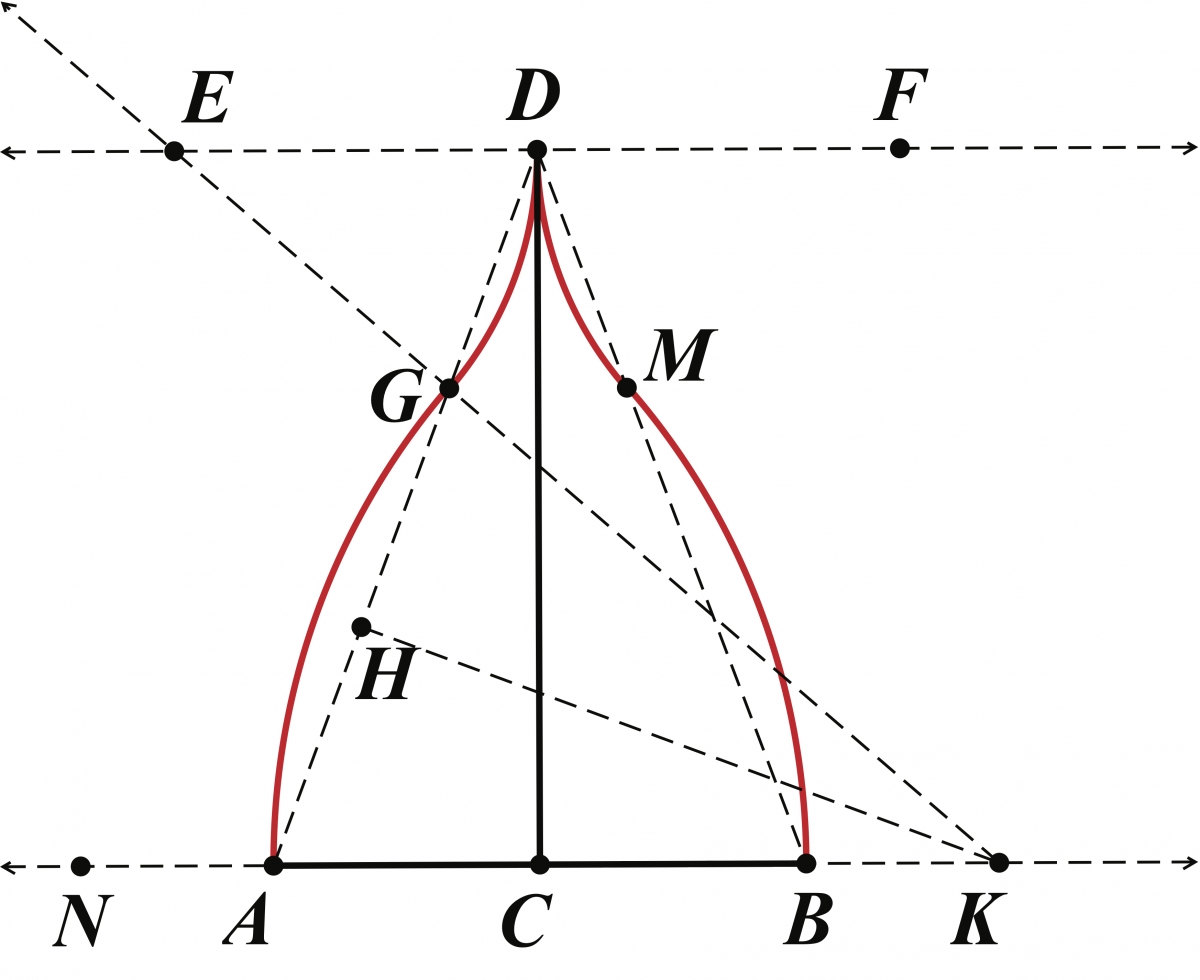
We now take a look at one of Sykes’ earlier constructions, taken from her article “Some Practical Applications of Elementary Geometry,” which she began by commenting, “The mind ... must be trained to effective doing through the solution of practical problems” [29]. For her first example of a real-world problem from mechanical drawing she gave the construction of a particular type of ogee arch called a Persian arch. An ogee arch consists of two ogee curves meeting at an apex. An ogee curve bears a resemblance to the letter S in that it consists of two arcs of opposite concavity. Three ogee arches are found in the close-up image of the Yorkshire church shown in Figure 4. The largest ogee arch appears above the large central window, the smallest is found above the door on the lower right, and another is found above the main entrance door.

Figure 4: Beverley Minster in Yorkshire, England. Wikimedia Commons.

In her Source Book that appeared six years after this article, Sykes presented the constructions of four other types of ogee arches and provided some historical and architectural context:

The ogee arch is much used on Turkish buildings, and is common as an ornamental feature in the late Gothic. It is very generally used in canopies and gables in the masses of ornament that cover the inside and outside of the later Gothic cathedrals. Half of it is sometimes used for veranda rafters, and for roofs of bay and oriel windows [40].

The construction she presented in the 1906 article is interesting in that, in addition to the traditional constructions of perpendicular and parallel lines, the infrequently encountered trisection of a segment of a given length is needed. Sykes’ directions are as follows with our comments added parenthetically in italics. The construction steps are illustrated in Figure 5.

• Given \(AB\) the span and \(CD\) the altitude. Draw the isosceles triangle \(\triangle ABD\).
• Divide \(AD\) into three equal parts. (That is, we have \(H\) and \(G\) on \(AD\) such that \(AH = HG = GD\).)
• Draw \(HK\) the perpendicular at the first point of division cutting \(AB\) at \(K\). (Thus, \(K\) lies on line \(AB\) and \(HK\) is perpendicular to \(AD\).)
• Draw \(KG\) (\(G\) the second point of division) cutting \(EF\) at \(E\). \(EF\) is parallel to \(AB\) through \(D\). (In other words, let \(E\) be the intersection of the line \(KG\) and the parallel to \(AB\) through \(D\). Construct \(F\) on this parallel so that \(ED = FD\).)

 

Figure 5: The Persian arch.

• \(K\) is center and \(KA\) radius and \(E\) center and \(ED\) radius for arcs \(AGD\). (Here we have two arcs of circles, one with center \(K\) and radius \(KA\), and the other with center \(D\) and radius \(ED\). These circles meet at \(G\) where, together, arcs \(\widehat{AG}\) and \(\widehat{GD}\) form the left half of the Persian arch.)
• On right side of figure \(FD\) equals \(DE\) and \(AN\) equals \(BK\) and the arcs drawn. (Thus, for the right half of the arch, we must construct \(N\) on \(AB\) such that \(NC = KC\). Then, we construct two circles, one with center \(N\) and radius \(NB\), and the other with center \(F\) and radius \(FD\).)

Sykes ended the construction by posing the following unanswered question: “Why do arcs meet at \(G\) and \(M\)?” To see why the circle with center \(K\) and radius \(KA\) passes through \(G\), one should note that \(H\)  is the perpendicular bisector of \(AG\), and thus, \(AK = GK\). Furthermore, the similarity of triangles \(\triangle EDG\) and \(\triangle KAG\) guarantees that \(ED = EG\).

Now let’s take a closer look at Sykes’ A Source Book of Problems for Geometry Based upon Industrial Design and Architectural Ornament. In his review of the book, H. E. Cobb wrote, “The present volume is a welcome contribution to the endeavor to make the mathematical work in our schools more practical and tangible” [51]. In her preface Sykes began,

The author is fully aware of the danger involved in offering this book to teachers of geometry. At present there is a widespread tendency in education to substitute amusement for downright work. This temptation presents itself in varied and subtle forms to all teachers. ... A design which is not an easily recognized application of a known construction is certainly of doubtful value. ... But geometry gives, as no other subject can give, an appreciation of form as it exists in the material world, and of the dependence of one form upon another [40].

Sykes’ initial warning aside, we have found this book to be a great resource for exploring geometric constructions used in architectural designs. In over 1800 exercises, Sykes analyzed geometric patterns found in architectural elements from tilings to windows and arches. Each of the six chapters is devoted to a particular form or design. Buildings from across the globe provide examples of wall tilings, mosaics, parquet floors, stained glass, ironwork, trusses and arches. Two of the chapters are devoted to Gothic tracery, a term originally used to describe the elaborate stonework that supports the glass within a window opening. It has come to include designs found in similar architectural features cut or cast from stone, or carved in wood, such as open screens, parapets, and balustrades. Sykes also included examples of geometric design found in jewelry and needlework. Hundreds of beautiful diagrams of tilings, tracery, and arches are presented, often alongside an illustration of the building that inspired the problem. There are Roman and Byzantine mosaics, Moorish and Greek tilings, Gothic and Persian arches, and Arabic and Egyptian parquet floor designs. In her historical comments, Sykes noted the interconnectedness and ubiquitousness of designs that span millennia, continents, and cultures. For example, the quadrifoil, while found in medieval Gothic designs, can also be seen in Chinese, Japanese and Native American decoration [40]. Here, we highlight five designs from Sykes’ book.

Figure 6: Parquet Flooring.

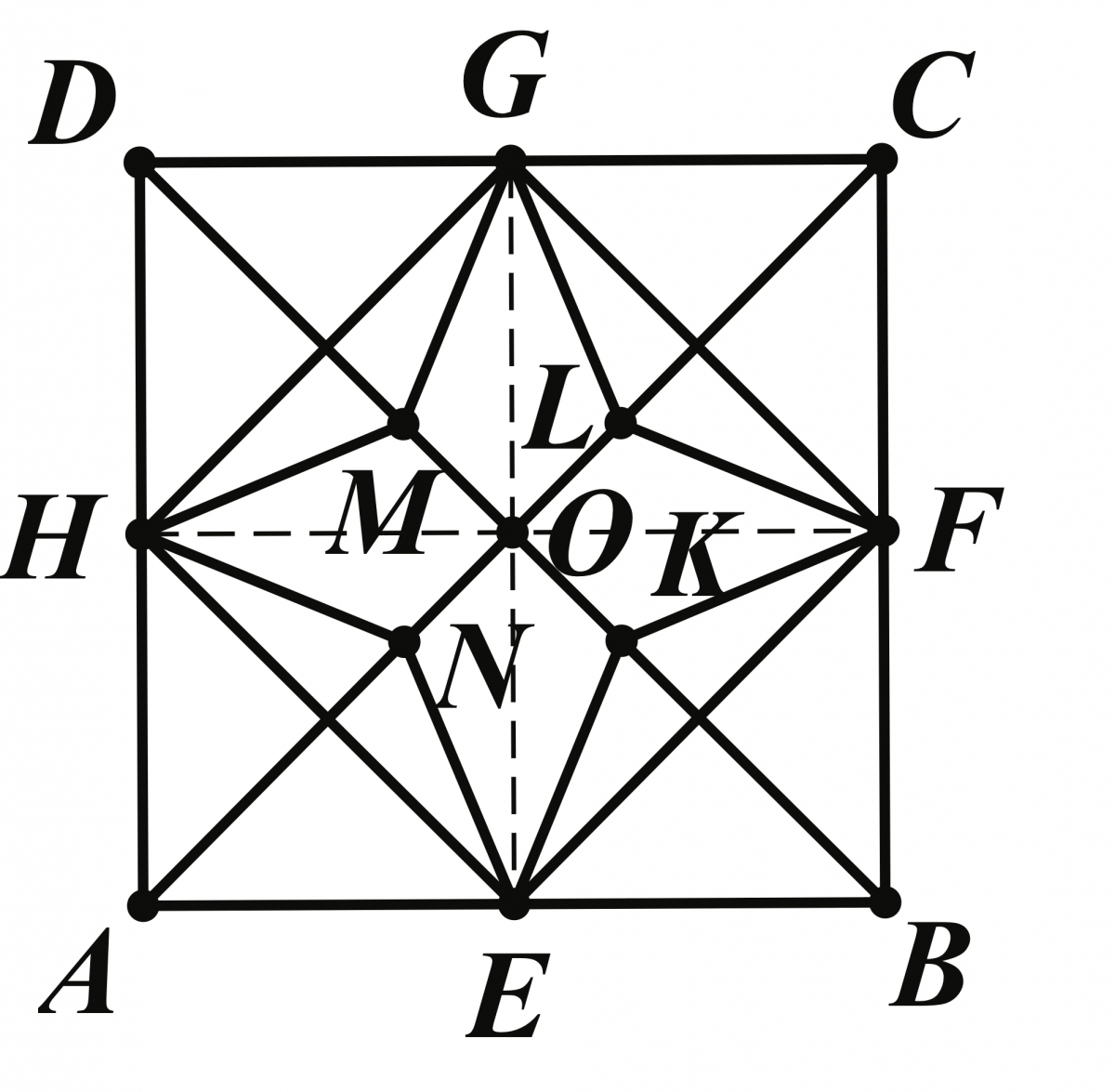
From page 59 of the Parquet Floor Designs chapter we have the example illustrated in Figure 6. This figure is a \(2 \times 2\) array of the individual tile shown in Figure 7. Sykes describes a single tile as follows: “\(ABCD\) is a square with diameters and diagonals. \(OK = OL = OM = ON\) and the points are joined as shown.” While use of the term diameter for a square is a bit unusual, in this case we take it to mean the segments joining the midpoints of opposite sides. The accompanying exercises include the following:

1. Prove that:
   1. \(EK = KF = FL\), etc.;
   2. \(\angle MHN = \angle NEK = \angle KFL\), etc.;
   3. \(ONEK\) and \(OKFL\) are congruent.
2. If \(AB = 12\) and \(OK = 3\), find the area of the star \(EKFLG\) etc.
3. If \(OK =\frac{OB}{n}\), compare the areas of \(\triangle EKO\) and \(\triangle EBO\), and prove that the area of the star is \(\frac{1}{n}\) that of the square \(ABCD\).

Figure 7: Individual Tile for Parquet Flooring.

A total of eleven exercises are associated with this tile design. Notice that the length of OK is not prescribed and can be any positive value that is less than half of \(OB\). As a special case, Sykes considers when EK, KF, FL, etc. bisect the angles \(\angle OEF\), \(\angle OFE\), \(\angle OFG\), etc., respectively. As shown in the exercises below, this choice then determines the length of \(OK\). (This is, in fact, the case we have illustrated in Figure 7.) Sykes gave additional exercises for this case as given below. Here, the suggestions and answers are also provided by Sykes.

1. Prove that \(EK\), \(KF\), and \(OB\) are concurrent. Suggestion: The bisectors of the angles of a triangle are concurrent.

3. If \(AB = a\), find
   1. the length of \(OK\) \(\left (\frac{a}{2}(\sqrt{2}-1)\right) \);
   2. the area of \(EKFLG\) etc. \(\left ( \frac{a^2}{2}(2-\sqrt{2})\right) \);
   3. and of \(EKFB\) \(\left (\frac{a^2}{8}\sqrt{2}\right )\);.

Our next three examples are also designs based on a square and are found in three different sections of Chapter III. We have included interactive GeoGebra applets for each.

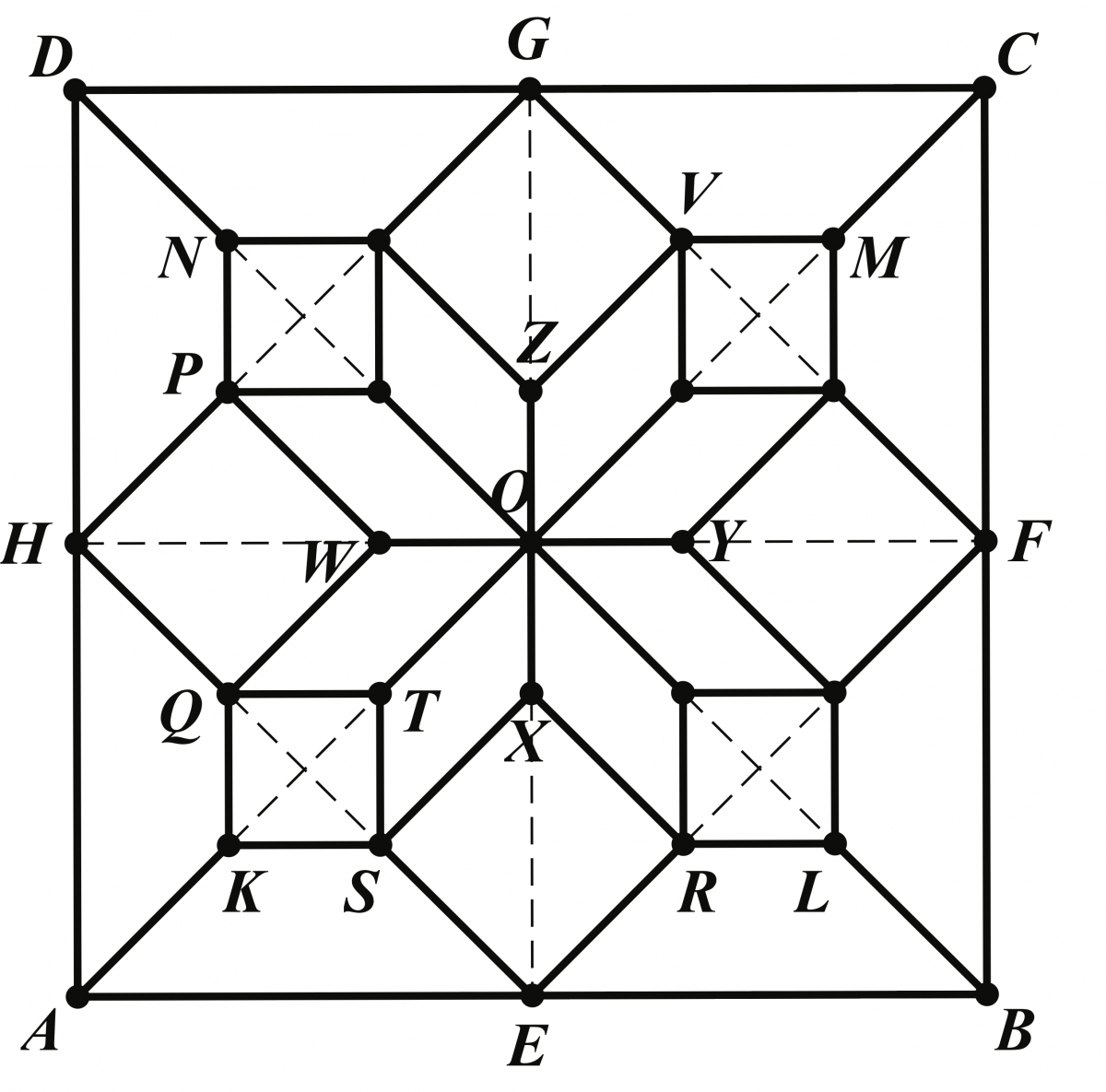
The first of these, shown in Figure 8, is one tile of a linoleum design found on page 75 in the section Designs based on octagons within squares. For this tile Sykes wrote “\(ABCD\) is a square, \(AR = VB = BU\), etc., and the points are joined as indicated.” Here, length \(AR\) is allowed to vary, as demonstrated by the GeoGebra applet found in Figure 9. Many of the exercises are focused on the special case when octagon \(EFGHKLMN\) (in Figure 8) is regular.

Figure 8: Linoleum Design.

Figure 9: Applet for design from Figure 8.

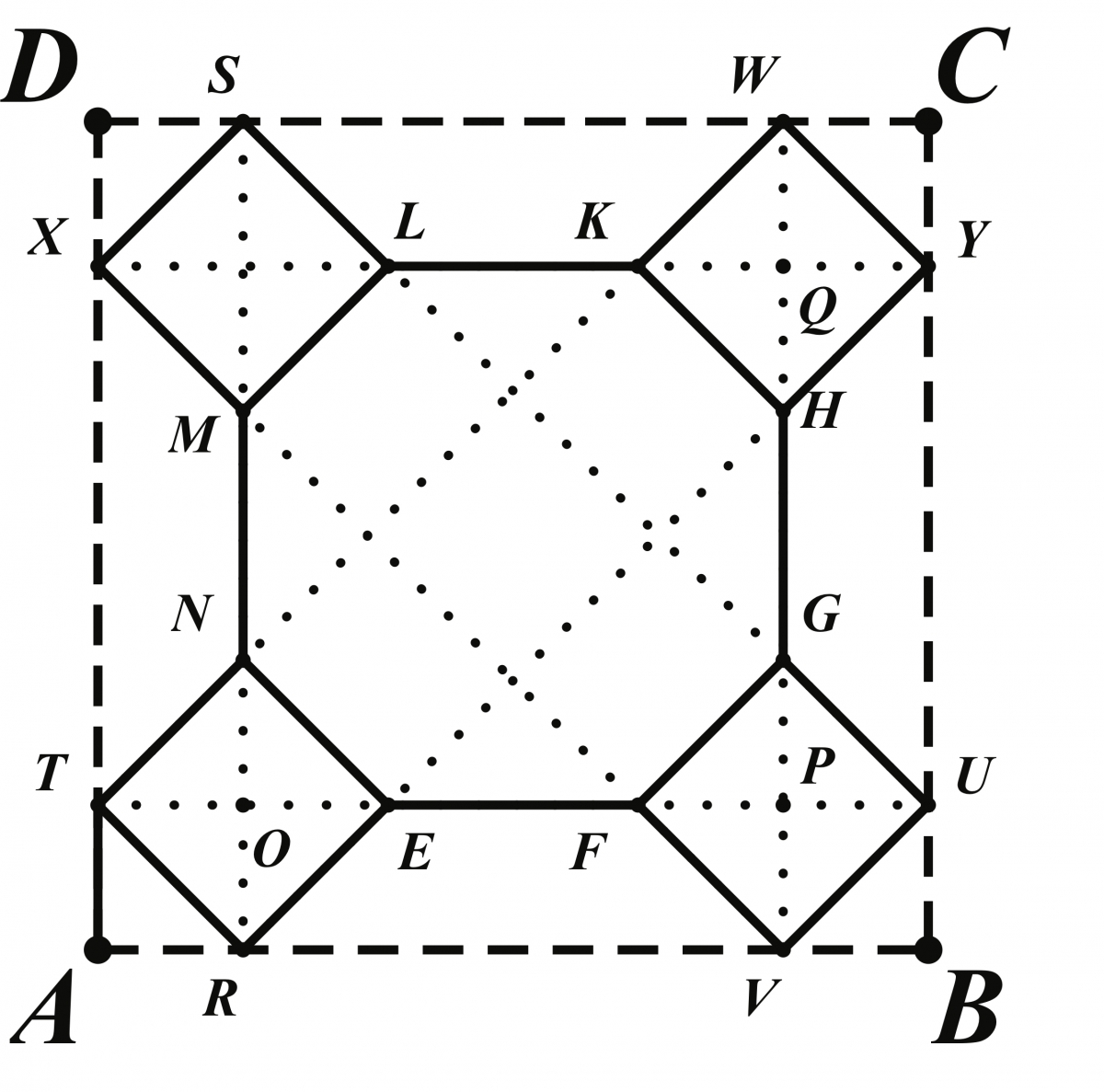
Our third example from the Source Book is another parquet floor tile, as illustrated in Figure 10, and comes from page 92 in the section Designs containing eight-pointed stars. For this figure, Sykes described: “\(ABCD\) is a square. \(E\), \(F\), \(G\), and \(H\) are the middle points of the sides. \(OK = OL = OM = ON\). The squares \(EFGH\)and \(KLMN\) are drawn. Points \(Q\) and \(V\), \(P\) and \(R\), etc., also \(K\) and \(L\), \(V\)and \(R\), \(K\) and \(N\), etc., are joined. Here, length \(AK\)may be any positive value less than half of \(AO\), as demonstrated by the GeoGebra found in Figure 11.

Figure 10: Parquet Flooring.

Figure 11: Applet for design from Figure 10.

Our fourth example, as illustrated in Figure 12, is a tile design from a counter railing that can be found on page 125 in the section Designs formed from line-segments and circle-arcs. Here, Sykes explained “\(ABCD\) is a square with diameters \(EG\) and \(FH\) and diagonals \(AC\) and \(BD\). \(KE = EM = FN = FQ\), etc.; and \(\angle EAB =\angle EBA = \angle FBC = \) \(\angle FCB = \angle GCD\), etc.” There are two choices for this design. The angle \(\angle EAB \) may be any positive angle less than \(45^o\). In Figure 12 we have chosen to bisect \(\angle CAB\). Furthermore, length \(AK\) may vary, as demonstrated by the GeoGebra applet in Figure 13. Like the exercises from our first tile design example, the associated exercises for the previous three examples also include length and area determinations for specific cases of the design.

Figure 12: Tile for counter railing design.

Figure 13: Applet for design from Figure 12.

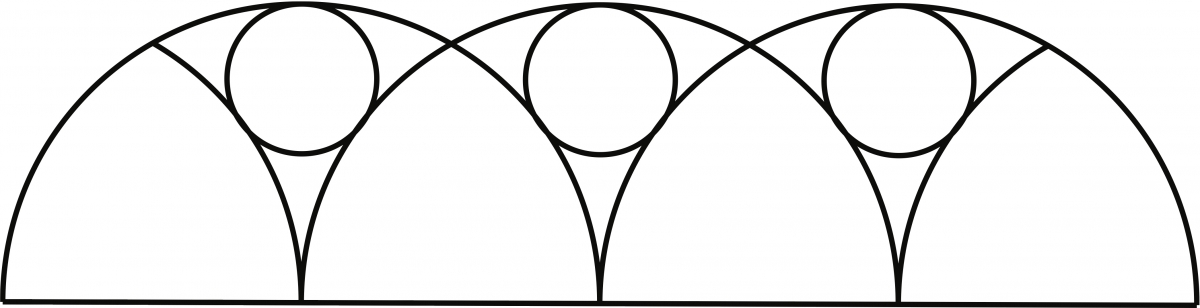
For our final example, we highlight one of the many beautiful illustrations of Gothic tracery. This design, shown in Figure 14, is found on page 269 in the subsection Forms containing tangent circles: algebraic analysis. Here, we start with a semicircle. Sykes described the construction as follows: “\(AB\) is the diameter of the semicircle \(ACB\). \(A\) and \(B\) are the centers and \(\frac{1}{2} AB\) the radius for the arcs \(DE\) and \(DF\). Circle \(O\) is tangent to the arcs as shown.” By tangent, Sykes meant that the circle with center \(O\) touches both the arcs \(DE\) and \(DF\), as well as the semicircle \(ACB\). For this design, as the title of the subsection suggests, we will need algebra in addition to geometry in order to construct the necessary tangent circle described above.

Figure 14: From Great Waltham Church, Essex, England.

At first the reader may be unsure how to proceed when constructing the tangent circle, but Sykes provided the key to solving this problem in the following exercise with added suggestion: “If \(AB = s\), find the radius of circle \(O\). Suggestion: Let the radius of circle \(O\) be \(r\). \(\triangle ODB\) gives the equation, \[\left(\frac{s}{2}\right)^2+\left(\frac{s}{2}-r\right)^2=\left(\frac{s}{2}+r\right)^2."\] Solving for \(r\) in terms of \(s\) gives us \(r = s/8\). Sykes’ follow-up question asked the reader to “show how to construct the entire figure.”

An example of a wood carving with this semicircular design, as shown in Figure 15, can be found in St. Andrew’s Church in Folkingham, England.

Figure 15: Decorated blind tracery (c.1330) in a lower panel of the rood screen, the Church of St Andrew, Folkingham, Lincolnshire. (Photograph by Spencer Means, August 17, 2014, www.flickr.com/photos/hunky_punk/15885732179, licensed under the Creative Commons Attribution-Share Alike 2.0 Generic license.)

It is easy to see how to extend the designs given in our first four examples since each is based on a square. With a semicircle, while at first glance it may appear difficult to extend a single copy of the design, it is still possible as demonstrated by the three overlapping design copies shown in Figure 16.

Figure 16: Gothic Tracery: Forms containing tangent circles.

With over 450 drawings and illustrations and over 1800 exercises, we have barely scratched the surface of the breadth of available problems and historical references. We have included some of her other designs in our own geometry book [4], and we encourage the reader to seek out Sykes’ work [40] as it provides beautiful examples of how geometry is used in architecture and industrial design.

Sykes’ textbooks were well-received, earning positive reviews from the American Mathematical Monthly and The Mathematics Teacher [50, 51, 52, 53, 54]. In particular, of her Source Book, H.E. Cobb wrote, “As a supplementary book in the high school course in geometry this text will, in the writer’s opinion, prove of great value” [51]. Of her 1918 Plane Geometry text, The Mathematics Teacher review noted, “This book will prove interesting to all teachers who believe that geometry should train the pupils for original thinking” [53]. In a comparison of then-current geometry texts to find those that were particularly good at conveying problem-solving techniques, Truman Sharwell singled out Sykes and Comstock for their “excellent full analyses” in their 1922 edition of Plane Geometry [55]. The review of the 1933 revision of this text testified to its “usability,” and states further, “This textbook humanizes geometry, emphasizing its beauty and usefulness. Geometric reasoning is made more enjoyable by showing how it fits in with life experiences and situations” [54]. In the review of the 1994 reprint of the Source Book, Sykes‘ “painstakingly rigorous investigation of architectural design and ornamentation” with an “impressive supply of historical references” was deemed an “enduring and timeless classic” [52].

In a biographical note accompanying an article appearing in 1935, the School Science and Mathematics journal described Sykes as “a charter member of the Central Association of Science and Mathematics teachers” who was “one of Chicago’s most successful teachers of secondary mathematics” [26]. While her life’s work testifies to the great passion she brought to the teaching of mathematics, it is difficult to determine the personal effect Mabel had on her students. There is, however, one impressive piece of evidence attesting to her influence as a teacher.

William L. Hart (1892–1984) was a professor at the University of Minnesota for 43 years, sold over 2 million textbooks, and served as Vice President of the Mathematical Association of America. In 1986, Hart’s biographer wrote, “W.L. Hart was born on October 12, 1892. He attended the South Chicago High School, which had a superior curriculum, principal, and staff of teachers, including Mabel Sykes, a distinguished mathematics teacher to whom Hart gave credit for his success in the field” [12]. It is touching that fifty years after Mabel Sykes’ death, she was not only remembered, but acknowledged, for her tremendous and indelible influence seventy-five years after Hart’s high-school graduation and two years after his death. It is an amazing tribute to a woman who dedicated her life to mathematics education.

Figure 17: Bowen High School Mathematics Club (1915). Mabel Sykes on right in middle row.

As befits the lifetime they spent together, Mabel and Marion rest in the family plot they share with their parents, sister Winifred, and brother Walter James in Chicago’s Graceland Cemetery. The cemetery was designed by landscape architects with aesthetics in mind and is the resting place of many prominent Chicagoans, including Marshall Field, Philip Armour, and George Pullman. Most fittingly, some of Chicago’s renowned architects such as John Root, Louis Sullivan, and Ludwig Mies van der Rohe can also be found there, as well as James H. Bowen, the namesake of the high school where Mabel devoted four decades of her life to teaching mathematics.

[1] Alma College Centennial Book, 1877–1977. Edited by Katherine Dobson Riddell. St. Thomas, Ontario: Phibbs Printing World, 1977.

[2] Andreas, A.T. History of Chicago: From the Earliest Period to the Present Time. Volume 2. Chicago: The A. T. Andreas Company, 1885. books.google.com/books?id=F9A4AQAAMAAJ.

[3] The Canadian Almanac and Repository of Useful Knowledge for the Year 1894. Toronto: The Copp, Clark Company, 1893. archive.org/details/cihm_29677/page/n10/mode/2up.

[4] Carroll, Maureen T., and Elyn Rykken. Geometry: The Line and the Circle. Providence: AMS/MAA Press, 2018.

[5] Evenden, Edward Samuel. Teachers’ Salaries And Salary Schedules In the United States 1918–19. Washington, DC: The National Education Association, 1919.

[6] "Ex-Deacon Sykes Convicted." New York Times, March 11, 1888, p. 1.

[7] “Final report of the National Committee of Fifteen on Geometry Syllabus.” The Mathematics Teacher 5, no. 2 (1912): 46–131.

[8]  Green, Judy, and Jeanne LaDuke. Pioneering Women in American Mathematics: The Pre-1940 Phd’s. Providence: American Mathematical Society, 2009.

[9] “Miss Mabel Sykes Teacher for 39 Years, Dies at 70.” Chicago Tribune, February 8, 1938, p. 16.

[10] “Mr. Sykes's Transactions.” New York Times, December 11, 1886, p. 1.

[11] “Periods of Service of the Officers of the National Council of Teachers of Mathematics.” The Mathematics Teacher 47, no. 1 (1954): 22–40.

[12] Price, G. Baley. “William LeRoy Hart 1892–1984.” Mathematics Magazine 59, no. 4 (1986): 232–238.

[13] Proceedings of the Board of Education of the City of Chicago: July 17, 1895, to July 1, 1896. Chicago: John F. Higgins, 1896.

[14] “Reports of Meetings: Report of Meeting of Teachers of Mathematics of the Cook County and Chicago High School Association.” School Science and Mathematics 1 (1903): 38–40.

[15] Reports to the General Assembly of Illinois: 1892. Volume 1. Springfield, IL: H. W. Rokker, [1893]. books.google.com/books?id=7GRKAAAAMAAJ.

[16] Schreiber, E.W. “The First Quarter-Century of the Mathematics Section of the Central Association.” School Science and Mathematics 29 (1929): 366-374.

[17] Wellesley College Calendar 1887. The Wellesley College Catalogs, 124. Wellesley, MA: Wellesley College, 1887. repository.wellesley.edu/catalogs/124.

[18] Wellesley College Calendar 1888. The Wellesley College Catalogs, 125. Wellesley, MA: Wellesley College, 1888. repository.wellesley.edu/catalogs/125.

[19] Wellesley College Calendar 1889–1890. The Wellesley College Catalogs, 127. Wellesley, MA: Wellesley College, 1889. repository.wellesley.edu/catalogs/127.

[20] Wellesley College Calendar 1890–1891, The Wellesley College Catalogs, 128. Wellesley, MA: Wellesley College, 1890. repository.wellesley.edu/catalogs/128.

[21] The Wellesley College Magazine 1 (1892–1893).

[22] Wellesley College Record 1875–1912: A General Catalogue of Officers and Students. Wellesley, MA: Wellesley College, 1912. books.google.com/books?id=z1lIAAAAYAAJ.

[23] The Wellesley Prelude, Wellesley College, September 26, 1891. repository.wellesley.edu/prelude/72.

[24] Alumnae biographical file of Mabel Sykes, Wellesley College Class of 1891. Wellesley College Archives, Library and Technology Services, Wellesley, MA.

[25] Alumnae biographical file of Marion Sykes, Wellesley College Class of 1895. Wellesley College Archives, Library and Technology Services, Wellesley, MA.

[26] “Who’s Who in This Issue.” School Science and Mathematics 35 (1935): 121–122.

Articles Authored by Mabel Sykes

[27] Sykes, Mabel. “Aims and Methods in the Teaching of Plane Geometry.” School Science and Mathematics 1, no. S2 (June 1903): 76–79.

[28] Sykes, Mabel. “Radical and Conservative Elements in the Teaching of Mathematics.” The School Review 13, no. 1 (1905): 59–69.

[29] Sykes, Mabel. “Some Practical Applications of Elementary Geometry.” School Science and Mathematics 6 (1906): 367–370.

[30] Sykes, Mabel. “The Circumference of a Circle of Given Radius.” Scientific American, August 26, 1911, 72 (supplement 1860): 135.

[31] Sykes, Mabel. “The Case Against High School Mathematics.” School Science and Mathematics 17 (1917): 667–676.

[32] Sykes, Mabel. “A Note to Trigonometry Teachers.” School Science and Mathematics 25 (1925): 800.

[33] Sykes, Mabel. “Some Pedagogical Aspects of Geometry Teaching.” The Mathematics Teacher 20, no. 8 (1927): 466–472.

[34] Sykes, Mabel. “Note on Demons of Elementary Mathematics.” School Science and Mathematics 29 (May 1929): 533.

[35] Sykes, Mabel. “A Study of Individual Differences as They Effect Mathematics Classes.” The Mathematics Teacher 24, no. 3 (1931): 180.

[36] Sykes, Mabel. “The Problem of Individual Differences in Mathematics Classes.” The Mathematics Teacher 25, no. 6 (1932): 363–368.

[37] Sykes, Mabel. “Differentiated Assignments.” School Science and Mathematics 32 (November 1932): 863–869.

[38] Sykes, Mabel. “The Use of Original Exercises in Geometry.” The Mathematics Teacher 28, no. 1 (1935): 36–42.

[39] Sykes, Mabel. “Some Criticisms of Recent Ninth Grade Algebra Texts.” School Science and Mathematics 35 (February 1935): 153–160.

Books Authored or Co-authored by Mabel Sykes

[40] Sykes, Mabel. A Source Book of Problems for Geometry, Based Upon Industrial Design and Architectural Ornament. With the cooperation of H. E. Slaught and N. J. Lennes. Boston: Allyn and Bacon; Norwood, MA: Norwood Press,1912. Reprint, Palo Alto, CA: Dale Seymour Publications, 1994.

[41] Sykes, Mabel, and Clarence E. Comstock. Plane Geometry. Chicago: Rand McNally & Co., 1918. Reprint, 1922.

[42] Sykes, Mabel, and Clarence E. Comstock. Beginners’ Algebra. Chicago: Rand McNally & Co, 1922.

[43] Sykes, Mabel. Training Pupils to Do Algebra: A Handbook for the Sykes-Comstock Geometries. Chicago: Rand McNally & Co, 1922.

[44] Sykes, Mabel, and Clarence E. Comstock. Solid Geometry. Chicago: Rand McNally & Co., 1922.

[45] Sykes, Mabel, and Clarence E. Comstock. A Second Course in Algebra. Chicago: Rand McNally & Co., 1924.

[46] Sykes, Mabel, and Clarence E. Comstock. Answers for Beginners’ Algebra. Chicago: Rand McNally & Co, 1925.

[47] Sykes, Mabel, and Clarence E. Comstock. Key to Plane Geometry. Chicago: Rand McNally & Co., 1926.

[48] Sykes, Mabel, Clarence E. Comstock, and Charles M. Austin. Plane Geometry. New York: Rand McNally, 1932.

[49] Sykes, Mabel, Clarence E. Comstock, and Charles M. Austin. Solid Geometry. New York: Rand McNally, 1933.

Reviews of Books Authored by Mabel Sykes

[50] Cederberg, Judith N. Telegraphic Reviews, edited by Arnold Ostebee and Paul Zorn. The American Mathematical Monthly 101, no. 9 (1994): 927.

[51] Cobb, H. E. Review of Source Book of Problems for Geometry, by Mabel Sykes. The American Mathematical Monthly 20, no. 5 (1913): 164–165.

[52] Jensen, John M. Review of Source Book of Problems for Geometry, by Mabel Sykes. The Mathematics Teacher 87, no. 7 (1994): 573–574.

[53] The Mathematics Teacher 12, no. 4 (1920): 172.

[54] The Mathematics Teacher 26, no. 4 (1933): 250.

[55] Sharwell, Truman P. “New Trends in Geometry Textbooks.” School Science and Mathematics 27 (1927): 261–263.

Secretary Reports Authored by Mabel Sykes

[56] Sykes, Mabel. “Report of the Mathematics Section of Central Association of Science and Mathematics Teachers.” School Science and Mathematics 8 (1908): 70–74.

[57] Sykes, Mabel. “The Central Association of Science and Mathematics Teachers Algebra Report of 1907.” School Science and Mathematics 9 (1909): 114–120.

[58] Slaught, H.E., W. Betz, E. L. Brown, C. L. Bouton, F. Cajori, W. Fuller, W. W. Hart, H. E. Hawkes, E. R. Hedrick, F. E. Newton, H. L. Rietz, R. L. Short, D. E. Smith, E. R. Smith, and M. Sykes. “Provisional Report of the National Committee of Fifteen on Geometry Syllabus.” School Science and Mathematics 11 (1911): 509–531.

[59] Sykes, Mabel. “Report of the Meeting of the Mathematics Section of the Central Association of Science and Mathematics Teachers.” School Science and Mathematics 11 (1911): 82–85.

[60] Sykes, Mabel. “Chicago Geometry Syllabus.” School Science and Mathematics 13 (1913): 587–598.

[61] Sykes, Mabel. “The Mathematics Survey of the Chicago School System." School Science and Mathematics 15 (1915): 120–126.

[62] Sykes, Mabel. “Minutes of the Mathematics Section, Central Association.” School Science and Mathematics 16 (1916): 174–176.

[63] Sykes, Mabel. “Minutes of Mathematics Section.” School Science and Mathematics 19 (1919): 265–267.

Acknowledgments

We offer our special thanks to Robert Kuhel, Bowen High School Alumni Association Treasurer, for the yearbook photographs. We are also grateful to Rebecca Goldman, the College Archivist at Wellesley College, for scanning the biographical files of alumnae Mabel and Marion.

About the Authors

Maureen T. Carroll is a professor of mathematics at the University of Scranton where she has been teaching the history of mathematics for over twenty years. She received the 2005 Marten M. Hasse prize for expository writing and the 2013 James P. Crawford Award for Distinguished College or University Teaching. She has been collaborating with Elyn since they met as fellows in MAA’s Project NExT.

Elyn Rykken is a professor of mathematics at Muhlenberg College. She is a St. Olaf alum who earned her Ph.D. in dynamical systems from Northwestern University. She and Maureen were participants in the Institute in the History of Mathematics and Its Use in Teaching, funded by the NSF. Their book, Geometry: The Line and the Circle, was published at the end of 2018 in the AMS/MAA Textbook Series. Mabel Sykes appeared on their mathematical radar while writing this book.