Teaching and Learning the Trigonometric Functions through Their Origins
In this series, we present a collection of curricular units based on primary historical sources and designed to serve students as an introduction to the study of trigonometry. Each unit may be incorporated, either individually or in various combinations, into a standard course in College Algebra with Trigonometry, a stand-alone Trigonometry course, or a Precalculus course. These lessons have also been used in courses on the history of mathematics and as part of a capstone experience for pre-service secondary mathematics teachers.
Trigonometry is concerned with measurements of angles about a central point (or of arcs of circles centered at that point) and quantities, geometrical and otherwise, that depend on the sizes of such angles (or the lengths of the corresponding arcs). It is one of those subjects that has become a standard part of the toolbox of every scientist and applied mathematician. Why is it so valuable?
There is a key geometrical feature of the measurement of angles, or arcs that are traced out, about a point in the plane: as we might expect, the sizes of such angles (or the lengths of such arcs) grow as one end of the arc moves counterclockwise around its circle (while the other remains fixed); but when the moving point returns to the place of the fixed point after making a full turn around the circle, it continues to retrace the same path through another turn, and another and another as the angle/arc grows ever-larger. In other words, periodic behavior is at the core of the relationships between angles and arcs and the measurements we associate with them.

Diagram from 14th-century manuscript copy of Ptolemy's Almagest, folio 22 recto.
Manuscript owned and digitized by gallica.bnf.fr / Bibliothèque nationale de France.
As a consequence, wherever the mathematical description of cyclical phenomena is needed, trigonometric functions make appearances in pure mathematics and in applications of mathematics to the sciences. An introduction to trigonometry is a staple of the mathematics curriculum in high schools and colleges, many of whose students later study calculus and other forms of mathematical analysis in which periodic phenomena are explored.
It is the goal of the curricular units presented in this series to impart to students some of the story of where and how the central ideas of this subject first emerged, in an attempt to provide context for their study of this mathematical theory. Students who work through the entire collection of units will encounter six milestones in the history of the development of trigonometry. Our journey will span a vast interval of time, from some unidentifiable moment dating as far back as around 1000 BCE, to roughly the year 1500 CE. We will consider developments of the subject that took place in many different parts of the world: in ancient Mesopotamia; in Hellenistic Greece and Roman-era Egypt; in medieval India; in central Asia during the height of Islamic science; and in Renaissance Europe. The term “milestones'' is quite appropriate here, since we are only touching on a few moments in a long and complex history, one that brings us just to the edge of the modern scientific era in which we now live.
More specifically, each unit looks at one of the following episodes in the development of the mathematical science of trigonometry:
- the emergence of sexagesimal numeration in ancient Babylonian culture, developed in the service of a nascent science of astronomy;
- a modern reconstruction (as laid out in [Van Brummelen 2009]) of a lost table of chords known to have been compiled by the Greek mathematician-astronomer Hipparchus of Rhodes (second century, BCE);
- a brief selection from Claudius Ptolemy's Almagest (second century, CE) [Toomer 1998] in which the author (Ptolemy) shows how a table of chords can be used to monitor the motion of the Sun in the daytime sky for the purpose of telling the time of day;
- a few lines of Vedic verse by the Hindu scholar Varāhamihira (sixth century, CE) [Neugebauer and Pingree 1970/1972] containing the "recipe" for a table of sines as well as some of the methods used for its construction;
- passages from The Exhaustive Treatise on Shadows [Kennedy 1976], written in Arabic in the year 1021 by Abū Rayḥān Muḥammad ibn Aḥmad al-Bīrūnī, which include precursors to the modern trigonometric tangent, cotangent, secant and cosecant;
- excerpts from Regiomontanus' On Triangles (1464) [Hughes 1967], the first systematic work on trigonometry published in the West.

Woodcut showing Regiomontanus with an astrolabe, from the Nuremberg Chronicle by Hartmann Schedel (1493), folio 255 recto. Wikimedia image from copy owned by University of São Paulo, believed to be in the public domain.
Readers who want to learn more about the history of trigonometry are recommended to consult Glen van Brummelen's masterful The Mathematics of the Heavens and the Earth: The early history of trigonometry [Van Brummelen 2009] from which much of this work took inspiration.
The onscreen introduction for each individual unit to appear in this series will provide additional historical detail about the episode in question, a brief instructor guide specific to the goals and implementation of that particular unit, and a downloadable pdf of the unit itself that can be shared with students (after removing the Notes to Instructors section). Readers who want to see the entire Primary Source Project (PSP) from which these units are drawn can obtain that PSP, A Genetic Context for Understanding the Trigonometric Functions, without waiting for future installments to appear, from the website of the NSF-funded project TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS). LaTeX source code of the entire PSP and of each individual unit is also available directly from the author by request. The concluding chapter of this series will describe the various paths that instructors have followed in their implementation of these materials in the range of courses described in the opening paragraph of this introduction, and it will provide comments from instructors and students about their experiences on those journeys.
Teaching and Learning the Trigonometric Functions through Their Origins: Episode 1 – Babylonian Astronomy and Sexagesimal Numeration
Our series of curricular units based on primary sources begins near the start of recorded history, the early centuries of the second millennium BCE in Old Babylonia. (A link to a pdf copy of the curricular unit itself appears toward the bottom of this page.) The term ‘Babylonia’ is used by historians and archaeologists to refer to that region of the world which is now part of present-day Iraq and whose most prominent cultural center was the ancient city of Babylon. The map pictured below shows modern cities and country boundaries superimposed on locations of the most important ancient Mesopotamian sites, including those of the Old Babylonian period. These are concentrated in Lower Mesopotamia, where the Tigris and Euphrates Rivers empty into the northern end of the Persian Gulf. (The map shows modern place names in roman type with cities marked as white dots, whereas ancient place names—all just ruins today—are in italic type with sites marked as a triangle of dots.)
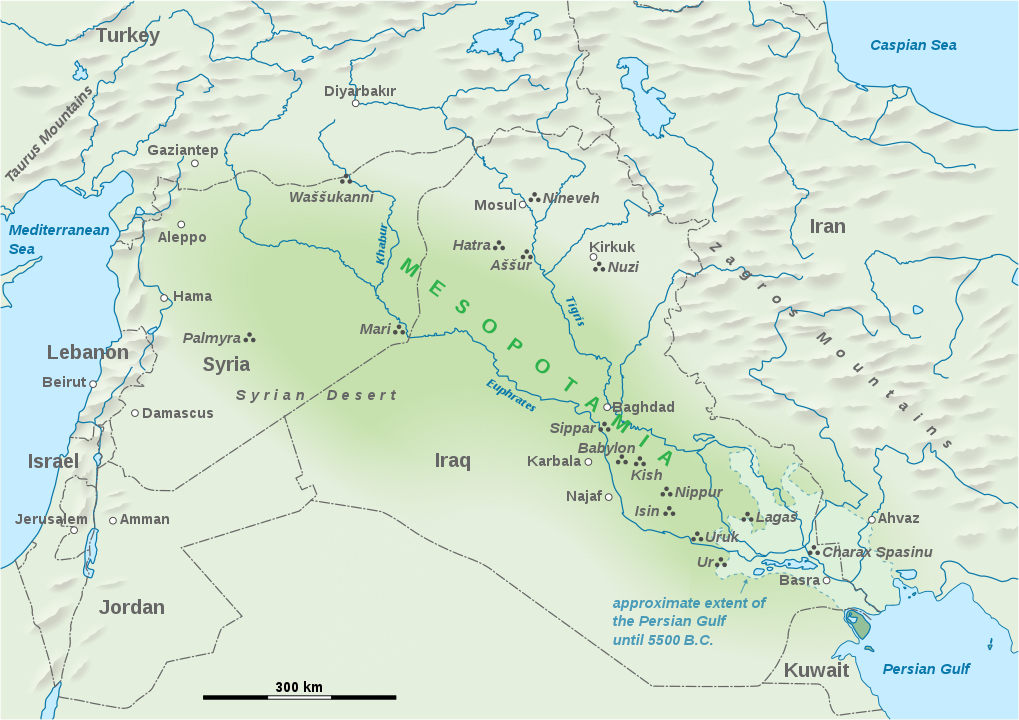
Key sites of ancient Mesopotamia superimposed on a modern map.
Map created by Wikigraphist Goran tek-en, 28 January 2014, and licensed under the
Creative Commons Attribution-Share Alike 4.0 International license.
In the Old Babylonian era, the earliest known systematic astronomical records were made. Some of these are recorded in a collection of clay tablets known today as the Enuma Anu Enlil. One such tablet fragment is pictured here:

Cuneiform tablet containing commentary on Enuma Anu Enlil.
Metropolitan Museum of Art, donated to Wikimedia Commons and made available under the
Creative Commons CC0 1.0 Universal Public Domain Dedication license.
Exercising the natural tendencies of human beings to notice and make use of patterns they observe in the world around them, early astronomers recognized the circular motions of the stars and planets in the sky and began to use numbers to describe these motions. The curricular unit Babylonian Astronomy and Sexagesimal Numeration, the first episode in our walk through the history of trigonometry, describes how Old Babylonian astronomers gave us the sexagesimal system of measurement of angles and circular arcs now known as degree measure. Students are introduced to sexagesimal numeration through its similarities with the decimal numeration with which they are already familiar. They also learn how this vestige of ancient history continues to ring through modern life via its presence in angle measure, in the geometry of the circle, and in the measure of time.
The unit Babylonian Astronomy and Sexagesimal Numeration (pdf) is ready for student use. It is meant to be completed in one 75-minute classroom period, plus time in advance for students to do some initial reading and time afterwards for them to write up their solutions to the tasks. This particular unit is unusual in that it does not include any primary source text. Instructors who wish to expose students to a primary source connected with the sexagesimal numeration system are encouraged to consider using the Primary Source Project Babylonian Numeration by Dominic Klyve, also from the TRIUMPHS collection. A brief set of instructor notes offering additional background and practical advice for the use of these materials in the classroom is appended at the end of the student version of these projects.
This unit is the first in the Convergence series Teaching and Learning the Trigonometric Functions through Their Origins. Although these classroom projects are posted here as parts of a series, each episode can also stand alone. Readers who want to see the entire Primary Source Project (PSP) from which these units are drawn can obtain that PSP, A Genetic Context for Understanding the Trigonometric Functions, without waiting for future installments to appear, from the website of the NSF-funded project TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS). The LaTeX source code of all TRIUMPHS projects, including the units to appear in this series, are available from the project authors by request.
Teaching and Learning the Trigonometric Functions through Their Origins: Episode 2 – Hipparchus’ Table of Chords
Millions of students worldwide learn trigonometry every year as a rite of passage in science, technology, engineering, and mathematics (STEM) education. They pass through a precalculus course, or even a course specifically focused on trigonometry, that is typically wedged between their introductions to the more fundamental skills in algebra and the more advanced training they will receive in differential and integral calculus. These experiences in the study of mathematics are generally directed to provide students with a working knowledge of the algebraic, geometric and analytic fundamentals that have become associated with the six trigonometric functions. Given the ever-escalating pressures to accelerate student training in these subjects, motivation for the study of trigonometry often receives short shrift. And when students present the natural question “why?”, the responses are meager and unprepared: “you’ll see when you study X later.”
So, who decided that degrees would be divided into sixties rather than tenths, as is everything else in scientific measurement? Is trig about triangles, or circles? What’s the deal with periodicity? Why is the sine function so important?
|
The classroom unit Hipparchus’ Table of Chords is the second of a series of six units in the Convergence series Teaching and Learning the Trigonometric Functions through Their Origins that attempts to provide students with a rich motivation for the study of trigonometry by presenting a series of episodes from the long history of the subject. These episodes contextualize the main ideas of trigonometry in the questions that earlier mathematicians addressed in developing the subject over thousands of years. In this unit, students are introduced to the basic elements of the geometry of the circle and the measure of its arcs, central angles and chords, whose interrelationships formed the foundation for trigonometry as a tool for Greek astronomy. Students read a brief excerpt from Claudius Ptolemy's Almagest (second century CE) that explains why the geometry of the circle was so important to astronomers. This is followed by an investigation of a (modern reconstruction of a) table of chords attributed to Hipparchus of Rhodes (second century, BCE), designed to show why and how degree measure works, as well as gently introduce students to the study of trigonometrical functions through an examination of a table of chords in a circle. |
 Hipparchus of Rhodes, Convergence Portrait Gallery. |
 Modern Reconstruction of Hipparchus' Table of Chords. |
The unit Hipparchus’ Table of Chords (pdf) is ready for student use. It is meant to be completed in two 50-minute classroom periods, plus time in advance for students to do some initial reading and time afterwards for them to write up their solutions to the tasks. A brief set of instructor notes offering additional background and practical advice for the use of these materials in the classroom is appended at the end of the student version of these projects. As mentioned above, the unit Hipparchus’ Table of Chords is the second in the Convergence series Teaching and Learning the Trigonometric Functions through Their Origins. Although these classroom projects are posted here as parts of a series, each episode has been redesigned to stand alone. Readers who want to see the entire Primary Source Project (PSP) from which these units are drawn can obtain that PSP, A Genetic Context for Understanding the Trigonometric Functions, without waiting for future installments to appear, from the website of the NSF-funded project TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS). The LaTeX source code of all TRIUMPHS projects, including the units to appear in this series, are available from the project authors by request. |
Teaching and Learning the Trigonometric Functions through Their Origins: Episode 3 – Ptolemy Finds High Noon in Chords of Circles
Chances are good that you have ready access to a cellphone, and that one of its main uses for you is as a timepiece. The time it tells is broadcast to you, and to everyone else served by your and other service providers, by a global GPS satellite system, which offers a highly accurate, synchronized regulation of time, down to the microsecond. This system of synchronized time telling is a feature (or curse?) of 21st-century life in much of the world that we generally take for granted. But clearly, it was not always that way. The classroom unit presented here, Ptolemy Finds High Noon in Chords of Circles, examines an early use of trigonometry, a branch of mathematics that forms a standard part of the mathematical training of students today, by drawing on primary historical sources related to the problem of constructing an effective sundial in the ancient world.

A simple gnomon sundial. Photo by Rich Luhr, reproduced under
Creative Commons license CC BY-NC-ND 2.0.
In the ancient world, the telling of time was an entirely local affair, of relevance only to small groups of people and restricted to small regions of the planet, not needing nearly the level of accuracy and synchrony that we come to expect in today’s world. In most circumstances, a general estimation of how high the Sun was in the sky, or which constellations were currently visible, was enough to guide people through their affairs. For the ancient Greeks, the paths of the Sun and stars, traced out against the great dome of the heavens, were reliably periodic and provided them with everything they needed for the kind of timekeeping that was useful to them.
|
In Ptolemy Finds High Noon in Chords of Circles, students read a brief excerpt from Claudius Ptolemy's important work on mathematical astronomy, the Almagest (second century CE). In this passage, Ptolemy made use of a table of chords that provides the measures of the lengths of chords across arcs in a reference circle for values of arclength from 0° to 180°, in steps of ½°. Ptolemy used these chord lengths in concert with a geometric model of the Sun in the sky and the shadow-casting gnomon at the ground to determine the precise lengths of shadows cast by the Sun at noon on the four first days of the seasons of the year at the latitude of the island of Rhodes. Through a series of tasks in the classroom unit, students prove and apply a proposition from Euclid’s Elements that was used by Ptolemy to connect the position of the sun on the ecliptic circle with the shadow of the gnomon on the earth. They then use basic sexagesimal arithmetic to verify Ptolemy’s results on the lengths of the gnomon’s shadow. This unit is one of a series of six classroom units in the Convergence series Teaching and Learning the Trigonometric Functions through Their Origins that attempts to provide students with a rich motivation for the study of trigonometry by presenting a series of episodes from the long history of the subject. These episodes work to contextualize the main ideas of trigonometry in the questions that earlier mathematicians addressed in developing the subject over thousands of years. The unit Ptolemy Finds High Noon in Chords of Circles (pdf) is ready for student use. It is meant to be completed in two 50-minute classroom periods, plus time in advance for students to do some initial reading and time afterwards for them to write up their solutions to the tasks. A brief set of instructor notes offering additional background and practical advice for the use of these materials in the classroom is appended at the end of the student version of these projects. |
 Diagram of armillary sphere in Peuerbach’s and Regiomontanus’s Latin translation of the Almagest. Mathematical Treasures, Convergence. |
As mentioned above, this is the third unit in the Convergence series Teaching and Learning the Trigonometric Functions through Their Origins. Although these classroom projects are posted here as parts of a series, each episode has been redesigned to stand alone. Readers who want to see the entire Primary Source Project (PSP) from which these units are drawn can obtain that PSP, A Genetic Context for Understanding the Trigonometric Functions, without waiting for future installments to appear, from the website of the NSF-funded project TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS). The LaTeX source code of all TRIUMPHS projects, including the units to appear in this series, are available from the project authors by request.
Teaching and Learning the Trigonometric Functions through Their Origins: Episode 4 – Varāhamihira and the Poetry of Sines
Until the twenty-first century, one typically learned about matters of general knowledge from printed books, such as the great Encyclopedia Britannica, that premier source of general information in the English language. Britannica was first published in 1771, and the second version of its fifteenth edition came out in 1985, a 30-volume series weighing a total of more than 125 pounds and indexing over 500,000 topics! This was to be its final printed edition: in 2003, its full contents were released on a single CD-ROM, a plastic disk 5 inches in diameter and weighing a bit more than half an ounce![1]
|
|
|
Now suppose you were faced with a large volume of mathematical information that you need to store and to pass along to users who come after you, but you do not know how to write. In an oral culture before the widespread use of writing, data storage problems like the one we have described here were often handled through the mechanics of poetry: metrical patterns of verse allowed the natural skills of human users to commit great amounts of information to memory for reliable transmission over time. The classroom unit, Varāhamihira and the Poetry of Sines, presented here introduces just such a process.
In the sixth century, the Hindu astronomer Varahāmihira (505–587 CE) composed a treatise called Pañcasiddhāntikā (The Five Canons), a summary of the Greek, Egyptian, Roman and Indian astronomy of his day. This astronomy carried on the Greek tradition that applied the geometry of the circle and sphere to work out the positions of the stars and planets in the heavens, a tradition that in its Greek past used to employ tables of chords in circles associated with the arcs they spanned, but that in Hindu science shifted to tables of sines of these arcs. To preserve the information in such a table over time, it was set to verse and recited. In just 11 lines, Varāhamihira encoded a full table of sines for 24 arcs from 0° to 90° (in multiples of 3°45´), as well as statements of a handful of trigonometric theorems.

Sanskrit verses from Varāhamihira’s Pañcasiddhāntikā (IV, 9-10).
In the classroom unit, students examine the first 9 lines of Varāhamihira’s verse, in English translation, and use the information encoded in these lines to build a partial table of sines for angles up to 60°. An optional appendix provides (in verses 10–11 of the source text) the information students need to extend that table to arcs of measure 90°. Because the context of the source text is astronomical, the unit includes a treatment of some basic astronomy having to do with the motion of the Sun through the zodiacal constellations. Students are also provided with a brief introduction to how circular arcs (and, equivalently, the central angles they span) are measured, as well as a discussion of the trigonometric innovation by Hindu astronomers that replaced the chord with the sine as the trigonometric quantity of chief interest
This classroom unit is one of a series of six units in the Convergence series Teaching and Learning the Trigonometric Functions through Their Origins, which attempts to provide students with a rich motivation for the study of trigonometry by presenting a series of episodes from the long history of the subject. These episodes work to contextualize the main ideas of trigonometry in the questions that earlier mathematicians addressed in developing the subject over thousands of years.
The unit Varāhamihira and the Poetry of Sines (pdf) is ready for student use. It is meant to be completed in two 50-minute classroom periods, plus time in advance for students to do some initial reading and time afterwards for them to write up their solutions to the tasks. A brief set of instructor notes offering additional background and practical advice for the use of these materials in the classroom is appended at the end of the student version of these projects.
Varāhamihira and the Poetry of Sines is the fourth in the Convergence series Teaching and Learning the Trigonometric Functions through Their Origins. Although these classroom projects are posted here as parts of a series, each episode has been redesigned to stand alone. Readers who want to see the entire Primary Source Project (PSP) from which these units are drawn can obtain that PSP, A Genetic Context for Understanding the Trigonometric Functions, without waiting for future installments to appear, from the website of the NSF-funded project TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS). The LaTeX source code of all TRIUMPHS projects, including the units to appear in this series, are available from the project authors by request.
[1] In fact, the 2000 launch of Wikipedia, the instantly editable online encyclopedia, has come to dominate the landscape of general-purpose reference works in English. Even optical disk technology for the written word has become obsolete with the migration of information storage to the “cloud.” In 2021, Wikipedia counted nearly 150,000 contributors worldwide responsible for more than 6 million articles on topics of all sorts.
Teaching and Learning the Trigonometric Functions through Their Origins: Episode 5 – al-Bīrūnī Does Trigonometry in the Shadows
It is generally well known that in the history of trigonometry, sine (and cosine) arose as adaptations, by Hindu astronomer-priests of the first millennium CE, of the earlier Greek notion of the chord of an arc in a circle. Since applications for which these chord lengths were needed often required determining half the chord of the doubled arc, in order to solve a certain right triangle, it was more useful to tabulate half-chords instead. Thus, the Hindu sine took on a life of its own; the cosine was nothing more than the sine of the complementary arc.
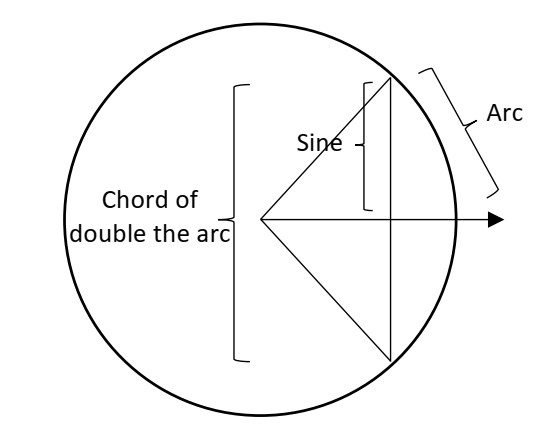
But what about the tangent, cotangent, secant and cosecant, to round out this trigonometric zoo of functions? How did these four trigonometric quantities arise?[1] It will come as no surprise to those familiar with the quirks of history that the Latin-based names we give them today were assigned centuries after they were first tabulated. The classroom unit al-Bīrūnī Does Trigonometry in the Shadows offered here employs excerpts from a text dating back to the golden era of Islamic mathematics to introduce students to the genesis of these quantities.
A scholar known mostly for his expertise in Hindu culture and science, Abū Rayhan Muhammad ibn Ahmad al-Bīrūnī (973–1048) wrote The Exhaustive Treatise on Shadows in 1021, exactly 1000 years before the preparation of this classroom unit. In Shadows, he provided a geometric and numerical analysis of the relation between the length of the shadow cast by a simple gnomon sundial and the corresponding arc of elevation of the Sun. Al-Bīrūnī considered two kinds of gnomon, one in which the gnomon is erected perpendicular to the ground, casting a “direct shadow,” and another in which the gnomon is mounted horizontally on a vertical wall, casting its “reversed shadow” on the wall itself. These shadow lengths, tabulated by al-Bīrūnī for a gnomon of unit length, are the quantities which centuries later would be renamed ‘cotangent’ and ‘tangent’, respectively.
The classroom unit opens with this simple problem of timekeeping based on shadows cast by the Sun. Students encounter al-Bīrūnī’s geometrical model for the shadow-casting gnomon, which makes it plain how the lengths of shadows are modeled by sides of right triangles and how tabulation of their lengths would be useful for more accurate daylight timekeeping. This realistic setting forms the foundation for what would later crystalize into the trigonometric quantities of tangent, cotangent, secant and cosecant. Examples of how al-Bīrūnī may have used this trigonometry to deal with the practical use of a shadow-casting clock are included throughout so that the mathematics is never too far from the astronomical context in which it arose.

A simple gnomon sundial.
Photo by Rich Luhr, reproduced under Creative Commons license BY-NC-ND 2.0.
This classroom unit is one of a series of six units in the Convergence series Teaching and Learning the Trigonometric Functions through Their Origins that attempts to provide students with a rich motivation for the study of trigonometry by presenting a series of episodes from the long history of the subject. These episodes work to contextualize the main ideas of trigonometry in the questions that earlier mathematicians addressed in developing the subject over thousands of years.
The unit al-Bīrūnī Does Trigonometry in the Shadows (pdf) is ready for student use. It is meant to be completed in two 50-minute classroom periods, plus time in advance for students to do some initial reading and time afterwards for them to write up their solutions to the tasks. A brief set of instructor notes offering additional background and practical advice for the use of these materials in the classroom is appended at the end of the student version of these projects.
al-Bīrūnī Does Trigonometry in the Shadows is the fifth in the Convergence series Teaching and Learning the Trigonometric Functions through Their Origins. Although these classroom projects are posted here as parts of a series, each episode has been redesigned to stand alone. Readers who want to see the entire Primary Source Project (PSP) from which these units are drawn can obtain that PSP, A Genetic Context for Understanding the Trigonometric Functions, without waiting for future installments to appear, from the website of the NSF-funded project TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS). The LaTeX source code of all TRIUMPHS projects, including the units to appear in this series, are available from the project authors by request.
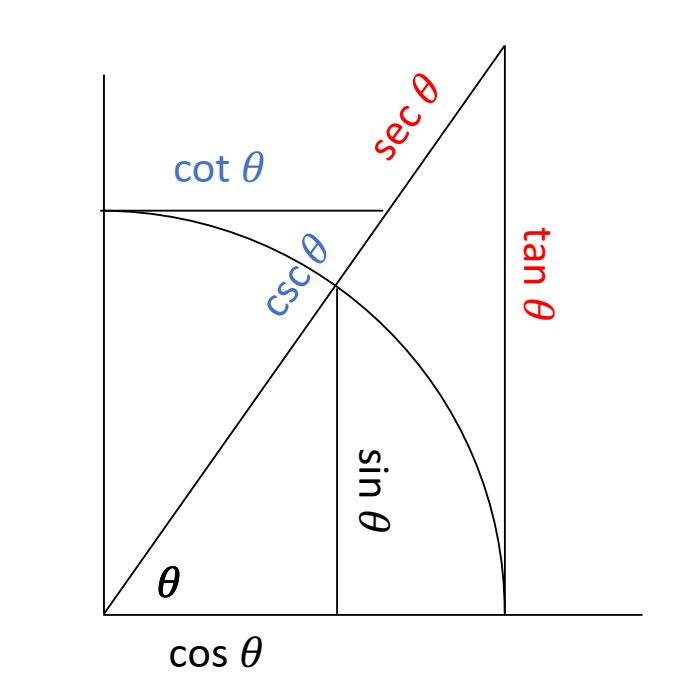
[1] I remember first considering this question myself, and I leapt to the natural conclusion that, because of how they were named, they must have identified other lines in the geometry of arcs in a unit circle. I recall learning to associate the trigonometric quantities with the segments in a diagram that combined three right triangles containing the same angle \(\theta\) (see the diagram below): one triangle inside the circle with hypotenuse equal to the unit radius and whose sides were the sine and cosine; one with base \(1\), whose side and hypotenuse are the tangent and secant; and one with vertical side \(1\) (so that the angle at the origin is complementary to \(\theta\)), whose side and hypotenuse are the cotangent and cosecant. While the names we give these segments today are related to how they appear in the diagram below, these quantities have a much older pedigree.
Teaching and Learning the Trigonometric Functions through Their Origins: Episode 6 – Regiomontanus and the Beginnings of Modern Trigonometry
In the preface to the first book of his two-volume history of trigonometry, The Mathematics of the Heavens and the Earth [2009] and The Doctrine of Triangles [2021], Glen Van Brummelen discussed how he decided where to divide the two volumes:
Trigonometry proper began with the origins of the Ptolemaic geocentric system, and a nice breaking point is found with the beginning of Copernicus’s heliocentric model [Van Brummelen 2009, p. xv].
But where Van Brummelen sees the transition from the early history of trigonometry to its modern phase in the shift of perspective between “the Earth-centered and Sun-centered universe” of Copernicus’ (literally) world-changing De revolutionibus (1543), the classroom unit Regiomontanus and the Beginnings of Modern Trigonometry featured in this article highlights a pedagogically more useful transition in the history of trigonometry through excerpts from a much less “revolutionary” work by Johannes Müller, better known by the name Regiomontanus (1436–1476).

Johannes Müller / Regiomontanus (1436–1476).
Woodcut from the Nuremberg Chronicle. Public domain.
Regiomontanus’ De triangulis omnimodis (On Triangles of Every Kind) was compiled decades earlier than De revolutionibus, in 1464, but it was not published until 1533. While it contained little brand-new mathematics, On Triangles was the first fully comprehensive treatment of trigonometry to appear in Europe. What makes it truly noteworthy, however, is what one will not find in its pages: astronomical problems. As Van Brummelen makes clear in The Mathematics of the Heavens and the Earth, the history of trigonometry up to the sixteenth century is to a large extent the history of astronomy. What we know today as trigonometry began as a collection of mathematical techniques, both geometrical and arithmetical, for addressing astronomical problems, such as: how to measure the elevation of the Sun in the sky; how to predict when a given star will rise, based on the regularity of its revolutions about an Earth-based observer; or when an eclipse (solar or lunar) should occur. Ancient mathematician-astronomers recognized that these questions could be handled by coordinating the measures of arcs along circles with the measures of chords across those arcs. Later, they found that it was more efficient to tabulate not the measures of chords, but measures of half-chords (sines).

From the title page of De triangulis (Basel, 1533). Mathematical Treasures, Convergence.
What Regiomontanus accomplished in On Triangles was essentially a reorientation of trigonometry away from its primary connection with astronomy and toward a resettlement within mathematics, specifically the Euclidean geometry of triangles and circles. He saw that many trigonometric problems could be rephrased in terms of finding one or more missing angles or side lengths in a right triangle, so he recast the subject as the branch of mathematics whose function was to solve triangles.[1] As a result, one can draw a direct connection between On Triangles and modern trigonometry textbooks: both introduce the sine by means of right triangles. This is precisely the connection made in the classroom unit Regiomontanus and the Beginnings of Modern Trigonometry. The unit also presents examples of solving triangles from On Triangles that ask students to familiarize themselves with calculator functions for sine and inverse sine.
This classroom unit Regiomontanus and the Beginnings of Modern Trigonometry is one of a series of six units in the Convergence series Teaching and Learning the Trigonometric Functions through Their Origins that attempts to provide students with a rich motivation for the study of trigonometry by presenting a series of episodes from the long history of the subject. These episodes work to contextualize the main ideas of trigonometry in the questions that earlier mathematicians addressed in developing the subject over thousands of years.
The unit Regiomontanus and the Beginnings of Modern Trigonometry (pdf) is ready for student use. It is meant to be completed in two 50-minute classroom periods, plus time in advance for students to do some initial reading and time afterwards for them to write up their solutions to the tasks. A brief set of instructor notes offering additional background and practical advice for the use of these materials in the classroom is appended at the end of the student version of the project.
Regiomontanus and the Beginnings of Modern Trigonometry is the sixth (and final) episode in the Convergence series Teaching and Learning the Trigonometric Functions through Their Origins. Although these classroom projects are posted here as parts of a series, each episode has been redesigned to stand alone. Readers who want to see the entire Primary Source Project (PSP) from which these units are drawn can obtain that PSP, A Genetic Context for Understanding the Trigonometric Functions, from the website of the NSF-funded project TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS). The LaTeX source code of all TRIUMPHS projects, including the units appearing in this series, are available from the project authors by request.
[1] To be sure, On Triangles was written for astronomers, but only as a mathematical preparation for doing astronomy. Indeed, in the note “To Readers” at the beginning of On Triangles, Regiomontanus remarked that:
[N]o one can bypass the science of triangles and reach a satisfying knowledge of the stars. . . . You, who wish to study great and wonderful things, who wonder about the movement of the stars, must read these theorems about triangles. Knowing these ideas will open the door to all astronomy and to certain geometric problems
It was only in the sixteenth century that the term trigonometry (literally “the measure of triangles”) began to be used to describe the subject, for by then it was differentiated from its astronomical “womb.”
Teaching and Learning the Trigonometric Functions through Their Origins: Acknowledgements
The development of the student projects presented in this series has been partially supported by the TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) project with funding from the National Science Foundation’s Improving Undergraduate STEM Education Program under Grants No. 1523494, 1523561, 1523747, 1523753, 1523898, 1524065, and 1524098. Any opinions, findings, and conclusions or recommendations expressed in this project are those of the author and do not necessarily reflect the views of the National Science Foundation.
Teaching and Learning the Trigonometric Functions through Their Origins: About the Author
Daniel E. Otero (Danny, to mostly everyone) is Associate Professor of Mathematics at Xavier University in Cincinnati, Ohio, where he has been on the faculty since 1989. A member of the MAA for over 40 years, he is currently Past Chair of the SIGMAA for History of Mathematics (HOM SIGMAA) and Section Representative to the MAA Congress for the Ohio Section. Trained as an algebraist and number theorist, Danny has been a student of the history of mathematics and an unabashed humanist since his school days and has devoted much of his scholarship to the use of history in the teaching of college level mathematics. He and Daniel J. Curtin (Northern Kentucky University) have co-organized the ORESME (Ohio River Early Sources in Mathematical Exposition) Reading Group since 1998; the group meets twice a year in the Cincinnati area to read influential texts drawn from the mathematics literature of long ago. Since 2015, he has been one of the seven Principal Investigators for the TRIUMPHS collaborative.
Teaching and Learning the Trigonometric Functions through Their Origins: References
Berggren, J. L. Episodes in the Mathematics of Medieval Islam. Springer, New York, NY, 2003.
Chereau, Fabien, and Guillaume Chereau. Stellarium Web. Stellarium Web Engine Project, 2020.
Hughes, Barnabas, O.F.M. Regiomontanus: On Triangles. University of Wisconsin Press, Madison, WI, 1967.
Katz, Victor. A History of Mathematics: an introduction. Addison Wesley, Reading, MA, second edition, 1998.
Katz, Victor, Annette Imhausen, Eleanor Robson, Joseph W. Dauben, Kim Plofker, and J. Lennart Berggren. The Mathematics of Egypt, Mesopotamia, China, India, and Islam: a Sourcebook. Princeton University Press, Princeton, NJ, 2007.
Kennedy, E. S. The Exhaustive Treatise on Shadows, by Abū Rayḥān Muḥammad ibn Aḥmad al-Bīrūnī. Institute for the History of Arabic Science, Aleppo, Syria, 1976.
Neugebauer, Otto, and David Pingree. The Pañcasiddhāntikā of Varāhamihira. Munksgaard, Copenhagen, Denmark, 1970/1972.
North, John. The Fontana History of Astronomy and Cosmology. Fontana Press, London, 1994.
Pedersen, Olaf. A Survey of the Almagest, with annotation and new commentary by Alexander Jones. Springer, New York, NY, 2011.
Plofker, Kim. Mathematics in India. Princeton University Press, Princeton, NJ, and Oxford, 2008.
Richards, E. G. Mapping Time: The calendar and its history. Oxford University Press, Oxford, 1998.
Suzuki, Jeff. Mathematics in Historical Context. Mathematical Association of America, Washington, DC, 2009.
Toomer, G. J. Ptolemy’s Almagest. Translated and annotated by G. J. Toomer; with a foreword by Owen Gingerich. Princeton University Press, Princeton, NJ, 1998.
Van Brummelen, Glen. The Mathematics of the Heavens and the Earth: The early history of trigonometry. Princeton University Press, Princeton, NJ, and Oxford, 2009.
Van Brummelen, Glen. The Doctrine of Triangles. Princeton University Press, Princeton, NJ, and Oxford, 2021.

