Converting the Old Babylonian Tablet ‘Plimpton 322’ into the Decimal System as a Classroom Exercise
For didactic purposes, we present a construction method for a decimal analogue of the Old Babylonian tablet Plimpton 322, produced by performing operations in base 10 (rather than in base 60), and designed so that all rational numbers are decimal fractions. This construction provides a nice classroom activity for prospective K–12 mathematics teachers, as well as high school students. The activity allows the participants to experience mathematics from the Old Babylonian period while remaining in the comfort zone of base 10. Working in a group through the interesting arithmetic algorithm behind the construction also consolidates several notions related to numbers and numeration systems, while providing opportunities to make and test mathematical conjectures. Last but not least, the activity allows the participants to better understand Plimpton 322 itself.
We also present historical and mathematical overviews of Plimpton 322 and offer practical suggestions for using the activity in the classroom. The activity itself can be downloaded by clicking here.
Converting the Old Babylonian Tablet ‘Plimpton 322’ into the Decimal System as a Classroom Exercise: Introduction
Because they are ancient, mysterious yet tangible objects that were frequently inscribed with mathematics, cuneiform tablets can provide appealing additions to secondary and undergraduate mathematics classrooms. With its apparent references to Pythagorean triples, the Old Babylonian clay tablet known as Plimpton 322 (so named for the collection at Columbia University in which it is held) may be a particularly tempting subject for a lesson. For instance, Daniel E. Otero has suggested activities for encouraging students to think about how numbers are expressed, to experiment with algorithms in arithmetic, and to further mastery of quadratic equations [Otero 2011]. Meanwhile, Amy Ackerberg-Hastings has used a version—in which the original values were replaced with familiar base-10 Pythagorean triples—to introduce mathematical and historical thinking in seven sections of a general-education science course on the history of science (see Appendix).
Even though debate persists among historians about what Plimpton 322 was actually designed to accomplish [e.g., Robson 2002; Britton, Proust, and Shnider 2011; Mansfield and Wildberger 2017], this tablet continues to stimulate a variety of classroom projects. In this article, we present an activity that guides students through the construction of a decimal analogue to the sexagesimal entries on the tablet, and we explain how such an activity is an enriching mathematical exercise that allows students to experience mathematics from the Old Babylonian period while remaining in the comfort zone of base 10.
Converting the Old Babylonian Tablet ‘Plimpton 322’ into the Decimal System as a Classroom Exercise: Historical Background of Plimpton 322
One of the most fascinating physical artifacts is a small Old Babylonian clay tablet labeled Plimpton 322, which is usually dated to around 1900–1600 BCE. The tablet contains a table of numbers that are written in the wedge-shaped cuneiform script typical of ancient Mesopotamian civilizations and that are expressed in sexagesimal (base 60) notation.

Figure 1: Plimpton 322, whose real size is approximately 13 cm × 9 cm × 2 cm. Wikimedia Commons.
As the photograph of the tablet suggests, table entries from the damaged areas of the tablet must be reconstructed, and historians are confident that we do not have the entire tablet because there is an obvious break on the left side. However, we do have table headings. (Some computational errors in the numbers have been corrected by math historians over the years.)
George Arthur Plimpton, who collected the tablet, purchased it from a dealer of antiquities, which means we do not know its provenance, or place of origin. (For other books and objects from Plimpton's collections, see Convergence's “Mathematical Treasures – The George Arthur Plimpton Collection.”) As a whole, the thousands of Mesopotamian tablets that have been analyzed indicate that those containing mathematics, but not obviously administrative or economic records, were created in schools that trained scribes to work in the bureaucracies that managed the royal dynastic empires that ruled in the region. Some were multiplication tables and lists of measurements that were copied and memorized by students; some were model examples prepared by teachers; some set out advanced mathematical problems; and the purpose for some remains unknown [Robson 2002; Bernard, Proust, and Ross 2014; Robson 2009; Collins 2008; Barrow-Green, Gray, and Wilson 2019].
Otto Neugebauer and Abraham Sachs were the first to look carefully at Plimpton 322 and realize its mathematics was interesting [Neugebauer and Sachs 1945]. In the past few decades, scholars have tended toward a consensus that the tablet's style and content resemble scribal school tables unearthed at Larsa, a major city-state in the south. Beyond those areas of agreement, though, debates continue over the exact reason why Plimpton 322 was inscribed. Some have theorized that it served as a resource for generating triangles that satisfy the Pythagorean Theorem; Robson and others argued that the values represent a descending list of reciprocal pairs that assisted with identifying the hypotenuses of right triangles whose short sides equal 1, given the long sides; Britton, Proust, and Shnider saw the tablet as setting out and solving a challenge problem on the sides and diagonals of rectangles; and Mansfield and Wildberger joined those who thought the tablet was used for trigonometry [Barrow-Green, Gray, and Wilson 2019; Robson 2002; Britton, Proust, and Shnider 2011; Mansfield and Wildberger 2017]. This ongoing scholarly discussion, of course, is one reason why mathematicians, educators, and students find this tablet so interesting.
Converting the Old Babylonian Tablet ‘Plimpton 322’ into the Decimal System as a Classroom Exercise: Mathematical Overview of Plimpton 322
Plimpton 322 attracted interest from scholars because the listed values appear to represent primitive Pythagorean triples (i.e., triples of strictly positive integers \((a,b,c)\) satisfying \(a^2+b^2=c^2\), and for which the three numbers have no common factors). The tablet contains four columns, representing (from right to left):
- the row number in the table;
- the hypotenuse of a right triangle;
- the shortest side of that triangle;
- either the square of the hypotenuse divided by the square of the longest side, or the square of the shortest side divided by the square of the longest side [Robson 2002].
Notice that the ambiguity in the leftmost column is minimal: the two proposed values differ by 1, and the question is whether we have 0 or 1 before the comma.
The degree measure of smallest angle in the right triangles associated with the table’s 15 rows is distributed quite well between 30 and 45 degrees (the following values are rounded):
44.8 ; 44.3 ; 43.8 ; 43.3 ; 42.1 ; 41.5 ; 40.3 ; 39.8 ; 38.7 ; 37.4 ; 36.9 ; 35.0 ; 33.9 ; 33.3 ; 31.9.
One explanation proposed for this feature of the table is that it derives from the fact that the regular sexagesimal integers (i.e., integers whose reciprocal has a terminating sexagesimal representation) are uniformly distributed among the integers [see, for example, de Solla Price 1964, p. 3].
The idea for the student activity that we describe in the next section was inspired by the theory proposed by Mansfield and Wildberger [2017], who argued that Plimpton 322 is an exact ratio-based trigonometric table that abandons the notion of angle. Indeed, working with sines and cosines corresponds to working with side lengths of right triangles, and the numbers given in the first column of Plimpton 322 are not approximations of the ratio recorded in that column. The main difficulty in appreciating this “exactness” aspect of Plimpton 322 comes from the fact that the mathematics underlying it is related to the base 60. The numbers in Plimpton 322 are rational numbers which have terminating sexagesimal representation. If we translate these numbers into base 10, most of them have non-terminating decimal representations because they are not decimal fractions. Thus simply getting a decimal translation (i.e., writing the given numbers in base 10) is not particularly illuminating.
For didactic purposes we present instead a construction method for a decimal analogue of Plimpton 322, produced by performing operations in base 10 (rather than in base 60), and where all rational numbers are decimal fractions. This construction provides a nice classroom activity for prospective K–12 mathematics teachers, as well as high school students. The activity guides students, working together in small groups, through an interesting arithmetic algorithm that produces primitive Pythagorean triples in a fashion consistent with the list of numbers on Plimpton 322. It also offers students opportunities to make and test mathematical conjectures as they work together through the various steps of the algorithm. Moreover, the activity consolidates several notions related to numbers and numeration systems (e.g., fractional versus decimal representations, different bases). Last but not least, the activity allows the students to better understand the famous tablet Plimpton 322 by removing the difficulty related to the base 60.
The complete student-ready activity sheet for constructing a decimal analogue of Plimpton 322 can be downloaded as a pdf in the next section of this article. Instructors who wish to first introduce the sexagesimal system to their students may also be interested in using the student activity “Babylonian Astronomy and Sexagesimal Numeration,” designed by Daniel E. Otero.
Converting the Old Babylonian Tablet ‘Plimpton 322’ into the Decimal System as a Classroom Exercise: Constructing the Decimal Analogue of Plimpton 322
As noted earlier, the purpose of Plimpton 322 has long been debated. It is also not certain how the displayed numbers were constructed. Our decimal analogue activity leads students through a construction method that is generally referred to as the “Reciprocal Pairs Algorithm.”[1] In this section, we outline and comment upon the steps of that algorithm, as they are presented in the student activity sheet. To download the activity sheet itself as a pdf, click here.
- We need to work with decimal fractions. We call a natural number regular for base 10, or a regular decimal, if its reciprocal has a terminating decimal representation. The regular decimal numbers up to 100 are:
1 , 2 , 4 , 5 , 8 , 10 , 16 , 20 , 25 , 32 , 40 , 50 , 64 , 80 , 100.
In the classroom activity, the pupils first find these numbers by themselves (as products of a power of 2 and a power of 5).
- We take certain pairs of regular decimal numbers \((r,R)\) from the above list and construct the rational numbers \[L=\frac{1}{2}\left(\frac{R}{r}-\frac{r}{R}\right) \,\,\,\,;\,\,\,\, H=\frac{1}{2}\left(\frac{R}{r}+\frac{r}{R}\right).\]
We want L to be positive and smaller than 1, for reasons that we explain below; this requirement implies that we must take \(r<R<(1+\sqrt{2})r\). Since we are only interested in the ratio \(\frac{r}{R}\), however, we get repetitions by varying \(r\) and \(R\). For these reasons, the table we provide in the classroom activity indicates five admissible pairs \((r,R)\) that give all the possible ratios for the list of regular decimals from step 1.
- We are also interested in the numerators of the reduced fractional forms of \(L\) and \(H\), which we refer to in the activity as their “least numerators” and denote by and respectively. We further make use of the least denominator \(d\) of \(H\), which is always equal to the least denominator of \(L\) (for reasons we discuss below). Furthermore, \(d\) is a regular decimal because it divides \(2rR\). These numbers (and also \(L\), \(H\), and their squares) are displayed in Figures 2 and 3, in fractional and decimal form respectively.
| \(L\) | \(H\) | \(L^2\) | \(H^2\) | \(n_L\) | \(d\) | \(n_H\) | row # |
| \(\frac{3}{4}\) | \(\frac{5}{4}\) | \(\frac{9}{16}\) | \(\frac{25}{16}\) | 3 | 4 | 5 | 1 |
| \(\frac{39}{80}\) | \(\frac{89}{80}\) | \(\frac{1521}{6400}\) | \(\frac{7921}{6400}\) | 39 | 80 | 89 | 2 |
| \(\frac{369}{800}\) | \(\frac{881}{800}\) | \(\frac{136161}{640000}\) | \(\frac{776161}{640000}\) | 369 | 800 | 881 | 3 |
| \(\frac{399}{1600}\) | \(\frac{1649}{11600}\) | \(\frac{159201}{2560000}\) | \(\frac{2719201}{2560000}\) | 399 | 1600 | 1649 | 4 |
| \(\frac{9}{40}\) | \(\frac{41}{40}\) | \(\frac{81}{1600}\) | \(\frac{1681}{1600}\) | 9 | 40 | 41 | 5 |
Figure 2: Values for the decimal analogue of Plimpton 322 (in reduced fractional form).
| \(L\) | \(H\) | \(L^2\) | \(H^2\) | \(n_L\) | \(d\) | \(n_H\) | row # |
| 0.75 | 1.25 | 0.5625 | 1.6625 | 3 | 4 | 5 | 1 |
| 0.2875 | 1.1125 | 0.23765625 | 1.23785825 | 39 | 80 | 89 | 2 |
| 0.46125 | 1.10125 | 0.2127515625 | 1.2127515625 | 369 | 800 | 881 | 3 |
| 0.249375 | 1.030625 | 0.062187890625 | 1.062187890625 | 399 | 1600 | 1649 | 4 |
| 0.225 | 1.025 | 0.50625 | 1.0506625 | 9 | 40 | 41 | 5 |
Figure 3: Values for the decimal analogue of Plimpton 322 (in decimal form).
What are the numbers \(L\) and \(H\)?
The rational numbers \(L\)and \(H\) can be interpreted as the short leg and the hypotenuse of a right triangle in which the length of the long leg equals 1. This means that \(L\)and \(H\) are strictly positive rational numbers satisfying \(L<1\) and the identity \(L^2+1=H^2\). Notice that \(L\) and \(H\) necessarily have the same least denominator because of this identity; to see this, one can first show that the least denominator of \(L\) is a possible denominator for \(H\) and then show that the same property holds by swapping \(L\) and \(H\).
How do we get Pythagorean triples?
Each row of the table can be interpreted as representative of a right triangle whose rational side lengths are \((L, 1,H)\). If we rescale such a triangle so that the side lengths are coprime integers, then we get the Pythagorean triple
\[(n_L,d,n_H).\]
The number \(n_L\) is the least numerator of L, d is the least denominator of \(L\) and of \(H\), and \(n_H\) is the least numerator of \(H\). A Pythagorean triple is called primitive if the three numbers have no common factor: by construction, \((n_L,d,n_H)\) is a primitive Pythagorean triple.
For example, the right triangle corresponding to the first row has side lengths (\(\frac{3}{4}\), 1, \(\frac{5}{4}\)), and we get the primitive Pythagorean triple (3, 4, 5). The distinctive aspect of the Pythagorean triples that we find is that, as observed above, the middle number (which is the least denominator of \(L\) and of \(H\) is a regular integer.
[1] This algorithm is used in the reconstruction method proposed in [Mansfield and Wildberger 2017]. It was originally proposed as a possible method of construction behind Plimpton 322 in [Bruins 1949] and also endorsed by a number of later scholars (e.g., [Buck 1980], [Schmidt 1980], [Friberg 1981], [Robson 2002]). Simoson [2019] presents an explanation of the algorithm via a “proof without words” figure, based on Old Babylonian cut-and-paste geometric constructions.
Converting the Old Babylonian Tablet ‘Plimpton 322’ into the Decimal System as a Classroom Exercise: Practical Remarks on the Classroom Activity
Prerequisites. Numeral bases different from 10, fractions (where the numerator and the denominator can be algebraic expressions), Pythagorean Theorem, basic algebra (for Exercises 8 and 9 only).
Timing. The students can work in groups so that they can share (and check) their computations. In this case the activity should not exceed 90 minutes. The choice of whether or how much use of a calculator should be permitted is left to the instructor.
An introduction. The teacher can present some short base 60 to base 10 conversion exercises; for example, (0.(15)) 60 = 15/60 = 1/4 = 0.25 and (0.(20))60 = 20/60 = 1/3 = 0.33333… The second example is a rational number with a terminating sexagesimal representation that is not a decimal fraction, and hence it has infinitely many digits in base 10. This will help students see why we wish to construct the decimal analogue of Plimpton 322 (rather than just converting the original numbers to base 10): we want the displayed numbers to be decimal fractions so that they are not approximations, but exact values.
Bonus Exploration Section. Some of the more theoretical aspects of the algorithm appear at the end of the activity. Since the main part of the activity does not rely on them, some or all of these explorations could be assigned as required or optional exercises for individual or small-group completion; the instructor could also discuss them with the whole class or omit them altogether.
Discussion. The instructor may ask some or all of the following questions to prompt deeper mathematical reflection. These can be discussed first in small groups before leading a whole-class discussion that brings up the ideas we note below.
- What are some characteristics of fractions (or rational numbers) that have a terminating sexagesimal representation? Rational numbers with a terminating sexagesimal representation are those for which the least denominator divides a power of 60. This means that the prime factors of the least denominator can only be 2, 3, and 5. In contrast, the prime factors of the least denominator of a rational number with a terminating decimal representation can only be 2 and 5. For this reason, rational numbers with a terminating sexagesimal representation appear more frequently than decimal fractions, because in the least denominator they can also have the prime factor 3.
- What could have been the purpose of Plimpton 322? Historians have several different ideas about this. One idea is that it was a teaching resource, for example a source of drill problems or the solution to a problem. Or it may have been a multiplication table. Or a list of measurements. Or a list of Pythagorean triples. It could also have been a sort of trigonometric table. In the actual Plimpton 322 tablet, we have 15 rows giving a list of quantities which may have been associated with 15 non-skinny right triangles whose long leg is 1. For any non-skinny right triangle we may rescale its sides so that the long leg is 1 and then approximate it with one on the tablet for computational purposes.
- In the activity worksheet, both fractional and decimal representations of numbers were used. What are the advantages and disadvantages of these two different representations? Students will have different answers to this question, depending in part on how they prefer to do computations themselves. The main point to raise is that different computations may be easier to carry out, or to carry out correctly, in one representation than in the other.
- What are some of the arithmetical properties of base 10 representations? Do any of these also hold when we write our numbers in base 60? Sample answers might include the fact that the last digit of a natural number written in base 10 is 0 if and only if the number is divisible by 10. Base 60 is similar since the last digit is 0 (or blank) if and only if the number is divisible by 60; when written in cuneiform, however, it can be difficult to tell whether the last digit is 0 or not. In base 10, the last digit of a natural number can also be used to tell if the number is even or odd: the last digit is even if and only if the number itself is even. In base 60, the symbols written in the last place can also be used to determine if the number is even or odd, but this is complicated when we write out the number in cuneiform since that system has only two different symbols (or wedge-shapes) representing ten and one respectively. In contrast, there are 10 different digit symbols in the Hindu-Arabic base 10 system that we use today, one for each value between 0 and 9. Extending this idea to base 60, we would need 60 different digit symbols, one for each value between 0 and 59.
Converting the Old Babylonian Tablet ‘Plimpton 322’ into the Decimal System as a Classroom Exercise: Acknowledgements and About the Authors
Acknowledgements
The authors heartily thank Convergence editors Amy Ackerberg-Hastings and Janet Heine Barnett who invested a considerable amount of time in transforming the initial draft of the paper into a nice article for Convergence. We thank them in particular for their considerable support and encouragement.
About the Authors
Converting the Old Babylonian Tablet ‘Plimpton 322’ into the Decimal System as a Classroom Exercise: References
Barrow-Green, J., Gray, J., and Wilson, R. 2019. The History of Mathematics: A Source-Based Approach. Vol. 1. AMS/MAA Textbooks Vol. 45. Providence, RI: MAA Press.
Bernard, A., Proust, C., and Ross, M. 2014. Mathematics Education in Antiquity. In Handbook on the History of Mathematics Education, edited by A. Karp and G. Schubring, 27–53. New York: Springer.
Britton, J. P., Proust, C., and Shnider, S. 2011. Plimpton 322: A Review and a Different Perspective. Archive for History of Exact Sciences 65(5), 519–566.
Bruins, E. M. 1949. On Plimpton 322, Pythagorean Numbers in Babylonian Mathematics. Koninklijke Nederlandse Akademievan Wetenschappen Proceedings 52, 629–632.
Buck, R. C. 1980. Sherlock Holmes in Babylon, American Mathematics Monthly 87, 335–345.
Collins, P. 2008. From Egypt to Babylon: The International Age 1550–500 BC. Cambridge: Harvard University Press.
de Solla Price, D. 1964. The Babylonian "Pythagorean Triangle" Tablet. Centaurus 10(1), 1–13.
Friberg, J. 1981. Methods and Traditions of Babylonian Mathematics: Plimpton 322, Pythagorean Triples and the Babylonian Triangle Parameter Equations. Historia Mathematica 8, 277–318.
Knuth, D. 1972. Ancient Babylonian algorithms. Communications of the ACM 15(7), 671–677.
Mansfield, D. F. and Wildberger, N. J. 2017. Plimpton 322 is Babylonian Exact Sexagesimal Trigonometry. Historia Mathematica 44, 395–419.
Neugebauer, O. and Sachs, A. J. 1945. Mathematical Cuneiform Texts. American Oriental Series, vol. 49. American Oriental Society, American Schools of Oriental Research.
Otero, D. E. 2011. Plimpton 322: The Pythagorean Theorem, More than a Thousand Years before Pythagoras. In Mathematical Time Capsules: Historical Modules for the Mathematics Classroom, edited by D. Jardine and A. Shell-Gellasch, 241–250. MAA Notes No. 77. Washington, DC: Mathematical Association of America.
Robson, E. 2002. Words and Pictures: New Light on Plimpton 322. American Mathematical Monthly 109, 105–120.
Robson, E. 2009. Mathematics Education in an Old Babylonian Scribal School. In The Oxford Handbook of the History of Mathematics, edited by E. Robson and J. Stedall, 199–227. Oxford: Oxford University Press.
Simoson, A. J. 2019. Extrapolating Plimpton 322. The College Mathematics Journal 50(3), 210–220. DOI: 10.1080/07468342.2019.1582990.
Schmidt, O. 1980. On Plimpton 322. Pythagorean Numbers in Babylonian Mathematics. Centaurus 24, 4–13.
Converting the Old Babylonian Tablet ‘Plimpton 322’ into the Decimal System as a Classroom Exercise: Appendix – Classroom Exercise on Interpreting a Table Inspired by Plimpton 322
Setting: Convergence co-editor Amy Ackerberg-Hastings used this exercise at the beginning of the second class meeting of a 100-level general-education course offered by a community college physical sciences department on the History of Science. Enrollees were generally looking for a way to meet their science requirement with a minimum of mathematics and lab work, while the department encouraged the use of teaching through hands-on activities. Trade-offs between historical accuracy and mathematical/scientific principles communicated at levels accessible to the students tended to favor the latter.
Rationale: She wanted to begin the course with an experience of how historians make sense of the past. Other objectives included conveying some of the unique challenges involved in writing the history of ancient mathematics and science (ideally, without worsening students’ anxieties about mathematics); showing how Western science has been built upon a deep foundation; and introducing one of the course themes, the nature and evolution of scientific methods.
Activity: Divide students into groups of 3–4 and distribute a copy of the following table. Instruct the groups to try to figure out the relationship(s) between the numbers in each row. Allow about 10 minutes for discussion.
| \(\frac{25}{16}\) | 3 | 5 | 1 |
| \(\frac{169}{144}\) | 5 | 13 | 2 |
| 1 | 1 | \(\sqrt{2}\) | 3 |
| 2 | 2 | \(\sqrt{8}\) | 4 |
| 3 | 3 | \(\sqrt{18}\) | 5 |
| 2 | 1 | \(\sqrt{5}\) | 6 |
| 3 | 2 | \(\sqrt{13}\) | 7 |
| 5 | 4 | \(\sqrt{41}\) | 8 |
Table of Pythagorean values, organized as on Plimpton 322.
Debriefing Session: Reconvene, and ask for a report from each group. Explain that the table contains values that satisfy the Pythagorean Theorem, \(a^2+b^2=c^2\), although they have been rearranged and \(b\) is only denoted indirectly. See the table with headings on the slide below. Students were generally most surprised and annoyed with themselves to realize they did not realize that the column on the right contained row numbers.
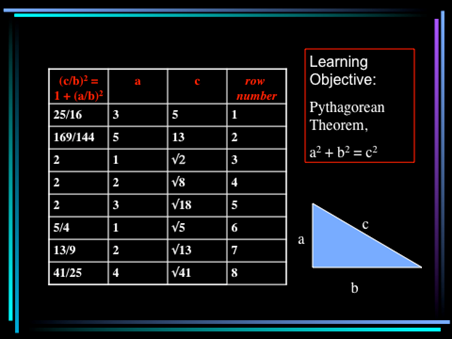
Classroom slide adding headings for the table used in the exercise.
Finally, Plimpton 322 (ca 1900–1600 BCE) can be introduced and briefly placed in the context of Mesopotamian science:
- Unlike the decimal numbers familiar to us and utilized in our exercise, the Mesopotamians used a sexagesimal numeral system.
- Mesopotamians wrote records on clay tablets with number symbols made from impressing wedges.
- The Mesopotamians used mathematical astronomy for agriculture and religion and astrology and setting a calendar, and they mapped the fixed stars and planets. They also left many clay tablets showing commercial transactions and problems sets for students.
- The Greeks believed that mathematics originated in Egypt and Mesopotamia.
Leave the students with questions such as: Is a list of examples scientific? How do historians figure out the history of ancient science? The debriefing and mini-lecture takes about 15–20 minutes, so that the entire activity requires around 30 minutes of in-class time.
As noted above, the students enrolled in the history of science course for which the activity was developed were nearly all subconsciously or overtly math-phobic, so Ackerberg-Hastings eventually simplified the table further to provide values for b in the left column instead of the \((c/b)^2+1=(a/b)^2\) that better corresponds to Plimpton 322. See the attached 2-part handout, which also features hints. Students were only slightly more successful at solving the puzzle, although they seemed to enjoy taking a few minutes to wrestle with it.
Follow-up: As homework, students can be assigned the following writing prompt:
Write a report (100–150 words) on the experiment in today’s class. Discuss how your group tried to determine the relationships between the numbers in the table, how your conclusions compared with those drawn by historians of Old Babylonian mathematics and astronomy, and the insights you gained into the history of science through this activity.